Two-Stage Holistic and Contrastive Explanation of Image Classification

The need to explain the output of a deep neural network classifier is now widely recognized. While previous methods typically explain a single class in the output, we advocate explaining the whole output, which is a probability distribution over multiple classes. A whole-output explanation can help a human user gain an overall understanding of model behaviour instead of only one aspect of it. It can also provide a natural framework where one can examine the evidence used to discriminate between competing classes, and thereby obtain contrastive explanations. In this paper, we propose a contrastive whole-output explanation (CWOX) method for image classification, and evaluate it using quantitative metrics and through human subject studies. The source code of CWOX is available at https://github.com/vaynexie/CWOX.

Handling Collocations in Hierarchical Latent Tree Analysis for Topic Modeling

Topic modeling has been one of the most active research areas in machine learning in recent years. Hierarchical latent tree analysis (HLTA) has been recently proposed for hierarchical topic modeling and has shown superior performance over state-of-the-art methods. However, the models used in HLTA have a tree structure and cannot represent the different meanings of multiword expressions sharing the same word appropriately. Therefore, we propose a method for extracting and selecting collocations as a preprocessing step for HLTA. The selected collocations are replaced with single tokens in the bag-of-words model before running HLTA. Our empirical evaluation shows that the proposed method led to better performance of HLTA on three of the four data sets tested.

Latent Tree Models for Hierarchical Topic Detection

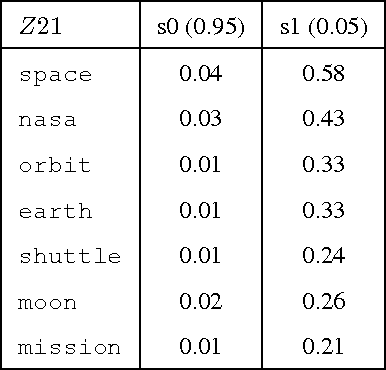
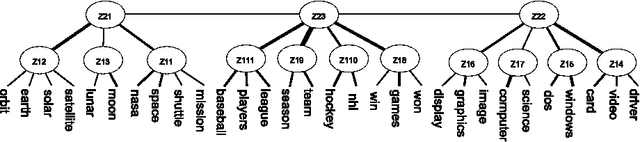
We present a novel method for hierarchical topic detection where topics are obtained by clustering documents in multiple ways. Specifically, we model document collections using a class of graphical models called hierarchical latent tree models (HLTMs). The variables at the bottom level of an HLTM are observed binary variables that represent the presence/absence of words in a document. The variables at other levels are binary latent variables, with those at the lowest latent level representing word co-occurrence patterns and those at higher levels representing co-occurrence of patterns at the level below. Each latent variable gives a soft partition of the documents, and document clusters in the partitions are interpreted as topics. Latent variables at high levels of the hierarchy capture long-range word co-occurrence patterns and hence give thematically more general topics, while those at low levels of the hierarchy capture short-range word co-occurrence patterns and give thematically more specific topics. Unlike LDA-based topic models, HLTMs do not refer to a document generation process and use word variables instead of token variables. They use a tree structure to model the relationships between topics and words, which is conducive to the discovery of meaningful topics and topic hierarchies.

Latent Tree Analysis

Latent tree analysis seeks to model the correlations among a set of random variables using a tree of latent variables. It was proposed as an improvement to latent class analysis --- a method widely used in social sciences and medicine to identify homogeneous subgroups in a population. It provides new and fruitful perspectives on a number of machine learning areas, including cluster analysis, topic detection, and deep probabilistic modeling. This paper gives an overview of the research on latent tree analysis and various ways it is used in practice.

Topic Browsing for Research Papers with Hierarchical Latent Tree Analysis

Academic researchers often need to face with a large collection of research papers in the literature. This problem may be even worse for postgraduate students who are new to a field and may not know where to start. To address this problem, we have developed an online catalog of research papers where the papers have been automatically categorized by a topic model. The catalog contains 7719 papers from the proceedings of two artificial intelligence conferences from 2000 to 2015. Rather than the commonly used Latent Dirichlet Allocation, we use a recently proposed method called hierarchical latent tree analysis for topic modeling. The resulting topic model contains a hierarchy of topics so that users can browse the topics from the top level to the bottom level. The topic model contains a manageable number of general topics at the top level and allows thousands of fine-grained topics at the bottom level. It also can detect topics that have emerged recently.

Progressive EM for Latent Tree Models and Hierarchical Topic Detection

Hierarchical latent tree analysis (HLTA) is recently proposed as a new method for topic detection. It differs fundamentally from the LDA-based methods in terms of topic definition, topic-document relationship, and learning method. It has been shown to discover significantly more coherent topics and better topic hierarchies. However, HLTA relies on the Expectation-Maximization (EM) algorithm for parameter estimation and hence is not efficient enough to deal with large datasets. In this paper, we propose a method to drastically speed up HLTA using a technique inspired by recent advances in the moments method. Empirical experiments show that our method greatly improves the efficiency of HLTA. It is as efficient as the state-of-the-art LDA-based method for hierarchical topic detection and finds substantially better topics and topic hierarchies.

A Model-Based Approach to Rounding in Spectral Clustering

In spectral clustering, one defines a similarity matrix for a collection of data points, transforms the matrix to get the Laplacian matrix, finds the eigenvectors of the Laplacian matrix, and obtains a partition of the data using the leading eigenvectors. The last step is sometimes referred to as rounding, where one needs to decide how many leading eigenvectors to use, to determine the number of clusters, and to partition the data points. In this paper, we propose a novel method for rounding. The method differs from previous methods in three ways. First, we relax the assumption that the number of clusters equals the number of eigenvectors used. Second, when deciding the number of leading eigenvectors to use, we not only rely on information contained in the leading eigenvectors themselves, but also use subsequent eigenvectors. Third, our method is model-based and solves all the three subproblems of rounding using a class of graphical models called latent tree models. We evaluate our method on both synthetic and real-world data. The results show that our method works correctly in the ideal case where between-clusters similarity is 0, and degrades gracefully as one moves away from the ideal case.