THESAURUS: Contrastive Graph Clustering by Swapping Fused Gromov-Wasserstein Couplings

Graph node clustering is a fundamental unsupervised task. Existing methods typically train an encoder through selfsupervised learning and then apply K-means to the encoder output. Some methods use this clustering result directly as the final assignment, while others initialize centroids based on this initial clustering and then finetune both the encoder and these learnable centroids. However, due to their reliance on K-means, these methods inherit its drawbacks when the cluster separability of encoder output is low, facing challenges from the Uniform Effect and Cluster Assimilation. We summarize three reasons for the low cluster separability in existing methods: (1) lack of contextual information prevents discrimination between similar nodes from different clusters; (2) training tasks are not sufficiently aligned with the downstream clustering task; (3) the cluster information in the graph structure is not appropriately exploited. To address these issues, we propose conTrastive grapH clustEring by SwApping fUsed gRomov-wasserstein coUplingS (THESAURUS). Our method introduces semantic prototypes to provide contextual information, and employs a cross-view assignment prediction pretext task that aligns well with the downstream clustering task. Additionally, it utilizes Gromov-Wasserstein Optimal Transport (GW-OT) along with the proposed prototype graph to thoroughly exploit cluster information in the graph structure. To adapt to diverse real-world data, THESAURUS updates the prototype graph and the prototype marginal distribution in OT by using momentum. Extensive experiments demonstrate that THESAURUS achieves higher cluster separability than the prior art, effectively mitigating the Uniform Effect and Cluster Assimilation issues

Community-Aware Efficient Graph Contrastive Learning via Personalized Self-Training

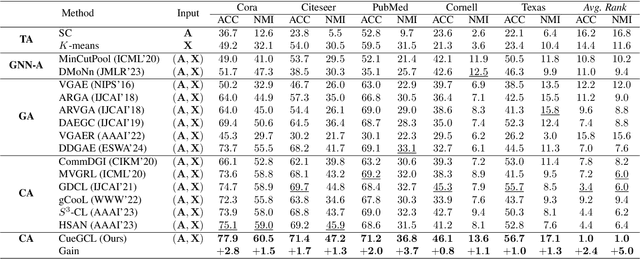
In recent years, graph contrastive learning (GCL) has emerged as one of the optimal solutions for various supervised tasks at the node level. However, for unsupervised and structure-related tasks such as community detection, current GCL algorithms face difficulties in acquiring the necessary community-level information, resulting in poor performance. In addition, general contrastive learning algorithms improve the performance of downstream tasks by increasing the number of negative samples, which leads to severe class collision and unfairness of community detection. To address above issues, we propose a novel Community-aware Efficient Graph Contrastive Learning Framework (CEGCL) to jointly learn community partition and node representations in an end-to-end manner. Specifically, we first design a personalized self-training (PeST) strategy for unsupervised scenarios, which enables our model to capture precise community-level personalized information in a graph. With the benefit of the PeST, we alleviate class collision and unfairness without sacrificing the overall model performance. Furthermore, the aligned graph clustering (AlGC) is employed to obtain the community partition. In this module, we align the clustering space of our downstream task with that in PeST to achieve more consistent node embeddings. Finally, we demonstrate the effectiveness of our model for community detection both theoretically and experimentally. Extensive experimental results also show that our CEGCL exhibits state-of-the-art performance on three benchmark datasets with different scales.

Hyper-Laplacian Regularized Concept Factorization in Low-rank Tensor Space for Multi-view Clustering

Tensor-oriented multi-view subspace clustering has achieved significant strides in assessing high-order correlations and improving clustering analysis of multi-view data. Nevertheless, most of existing investigations are typically hampered by the two flaws. First, self-representation based tensor subspace learning usually induces high time and space complexity, and is limited in perceiving nonlinear local structure in the embedding space. Second, the tensor singular value decomposition (t-SVD) model redistributes each singular value equally without considering the diverse importance among them. To well cope with the issues, we propose a hyper-Laplacian regularized concept factorization (HLRCF) in low-rank tensor space for multi-view clustering. Specifically, we adopt the concept factorization to explore the latent cluster-wise representation of each view. Further, the hypergraph Laplacian regularization endows the model with the capability of extracting the nonlinear local structures in the latent space. Considering that different tensor singular values associate structural information with unequal importance, we develop a self-weighted tensor Schatten p-norm to constrain the tensor comprised of all cluster-wise representations. Notably, the tensor with smaller size greatly decreases the time and space complexity in the low-rank optimization. Finally, experimental results on eight benchmark datasets exhibit that HLRCF outperforms other multi-view methods, showingcasing its superior performance.

Multi-view Graph Convolutional Networks with Differentiable Node Selection

Multi-view data containing complementary and consensus information can facilitate representation learning by exploiting the intact integration of multi-view features. Because most objects in real world often have underlying connections, organizing multi-view data as heterogeneous graphs is beneficial to extracting latent information among different objects. Due to the powerful capability to gather information of neighborhood nodes, in this paper, we apply Graph Convolutional Network (GCN) to cope with heterogeneous-graph data originating from multi-view data, which is still under-explored in the field of GCN. In order to improve the quality of network topology and alleviate the interference of noises yielded by graph fusion, some methods undertake sorting operations before the graph convolution procedure. These GCN-based methods generally sort and select the most confident neighborhood nodes for each vertex, such as picking the top-k nodes according to pre-defined confidence values. Nonetheless, this is problematic due to the non-differentiable sorting operators and inflexible graph embedding learning, which may result in blocked gradient computations and undesired performance. To cope with these issues, we propose a joint framework dubbed Multi-view Graph Convolutional Network with Differentiable Node Selection (MGCN-DNS), which is constituted of an adaptive graph fusion layer, a graph learning module and a differentiable node selection schema. MGCN-DNS accepts multi-channel graph-structural data as inputs and aims to learn more robust graph fusion through a differentiable neural network. The effectiveness of the proposed method is verified by rigorous comparisons with considerable state-of-the-art approaches in terms of multi-view semi-supervised classification tasks.

Learnable Graph Convolutional Network and Feature Fusion for Multi-view Learning

In practical applications, multi-view data depicting objectives from assorted perspectives can facilitate the accuracy increase of learning algorithms. However, given multi-view data, there is limited work for learning discriminative node relationships and graph information simultaneously via graph convolutional network that has drawn the attention from considerable researchers in recent years. Most of existing methods only consider the weighted sum of adjacency matrices, yet a joint neural network of both feature and graph fusion is still under-explored. To cope with these issues, this paper proposes a joint deep learning framework called Learnable Graph Convolutional Network and Feature Fusion (LGCN-FF), consisting of two stages: feature fusion network and learnable graph convolutional network. The former aims to learn an underlying feature representation from heterogeneous views, while the latter explores a more discriminative graph fusion via learnable weights and a parametric activation function dubbed Differentiable Shrinkage Activation (DSA) function. The proposed LGCN-FF is validated to be superior to various state-of-the-art methods in multi-view semi-supervised classification.