GAPNet: Granularity Attention Network with Anatomy-Prior-Constraint for Carotid Artery Segmentation

Atherosclerosis is a chronic, progressive disease that primarily affects the arterial walls. It is one of the major causes of cardiovascular disease. Magnetic Resonance (MR) black-blood vessel wall imaging (BB-VWI) offers crucial insights into vascular disease diagnosis by clearly visualizing vascular structures. However, the complex anatomy of the neck poses challenges in distinguishing the carotid artery (CA) from surrounding structures, especially with changes like atherosclerosis. In order to address these issues, we propose GAPNet, which is a consisting of a novel geometric prior deduced from.

Fitting tree model with CNN and geodesics to track vesselsand application to Ultrasound Localization Microscopy data

Segmentation of tubular structures in vascular imaging is a well studied task, although it is rare that we try to infuse knowledge of the tree-like structure of the regions to be detected. Our work focuses on detecting the important landmarks in the vascular network (via CNN performing both localization and classification of the points of interest) and representing vessels as the edges in some minimal distance tree graph. We leverage geodesic methods relevant to the detection of vessels and their geometry, making use of the space of positions and orientations so that 2D vessels can be accurately represented as trees. We build our model to carry tracking on Ultrasound Localization Microscopy (ULM) data, proposing to build a good cost function for tracking on this type of data. We also test our framework on synthetic and eye fundus data. Results show that scarcity of well annotated ULM data is an obstacle to localization of vascular landmarks but the Orientation Score built from ULM data yields good geodesics for tracking blood vessels.

Grouping Boundary Proposals for Fast Interactive Image Segmentation

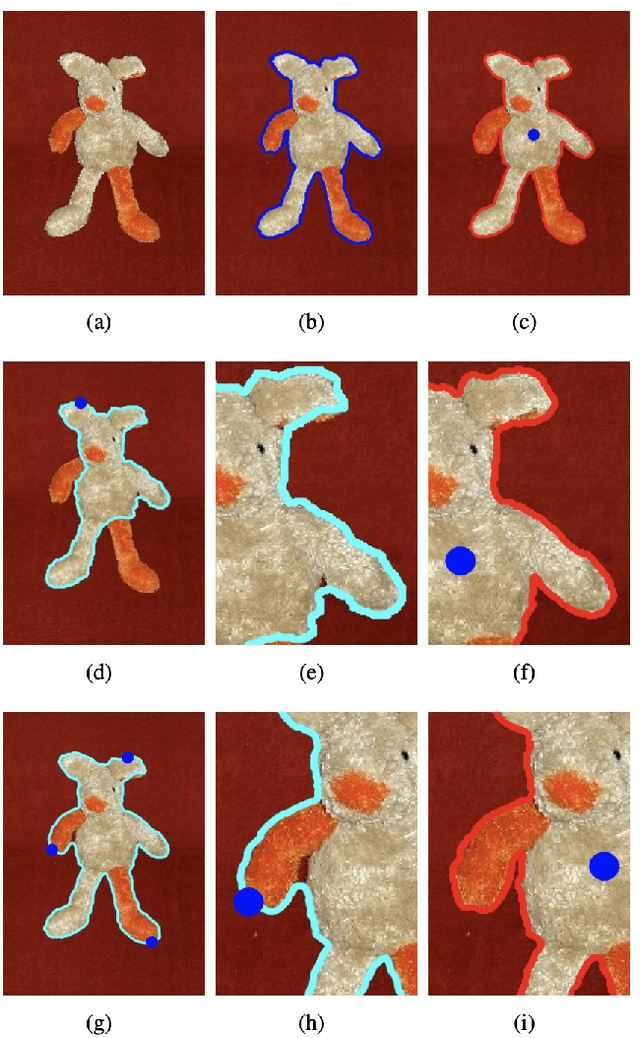
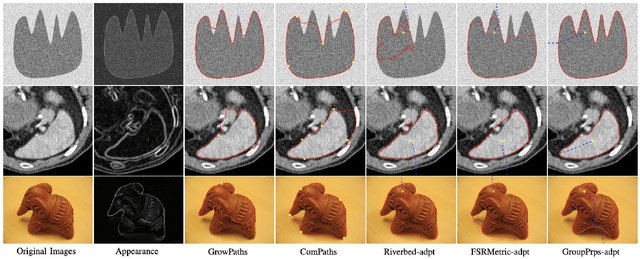
Geodesic models are known as an efficient tool for solving various image segmentation problems. Most of existing approaches only exploit local pointwise image features to track geodesic paths for delineating the objective boundaries. However, such a segmentation strategy cannot take into account the connectivity of the image edge features, increasing the risk of shortcut problem, especially in the case of complicated scenario. In this work, we introduce a new image segmentation model based on the minimal geodesic framework in conjunction with an adaptive cut-based circular optimal path computation scheme and a graph-based boundary proposals grouping scheme. Specifically, the adaptive cut can disconnect the image domain such that the target contours are imposed to pass through this cut only once. The boundary proposals are comprised of precomputed image edge segments, providing the connectivity information for our segmentation model. These boundary proposals are then incorporated into the proposed image segmentation model, such that the target segmentation contours are made up of a set of selected boundary proposals and the corresponding geodesic paths linking them. Experimental results show that the proposed model indeed outperforms state-of-the-art minimal paths-based image segmentation approaches.

Chan-Vese Attention U-Net: An attention mechanism for robust segmentation

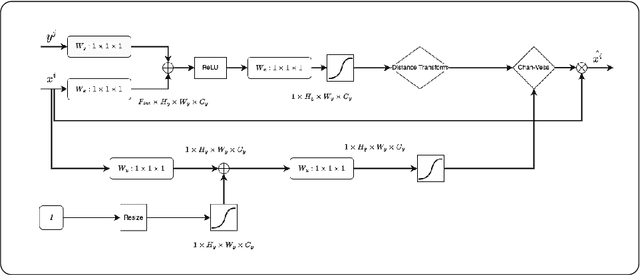
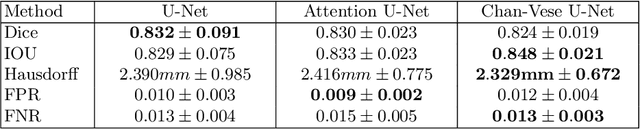
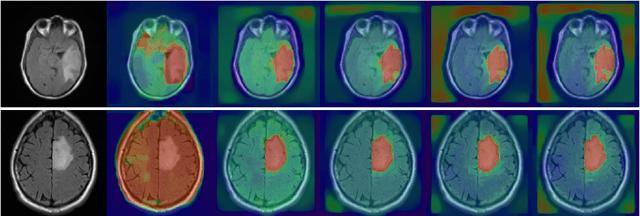
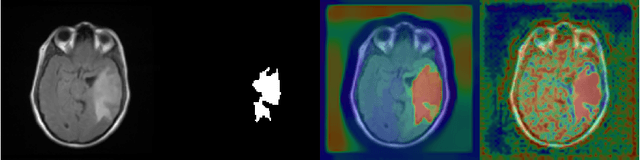
When studying the results of a segmentation algorithm using convolutional neural networks, one wonders about the reliability and consistency of the results. This leads to questioning the possibility of using such an algorithm in applications where there is little room for doubt. We propose in this paper a new attention gate based on the use of Chan-Vese energy minimization to control more precisely the segmentation masks given by a standard CNN architecture such as the U-Net model. This mechanism allows to obtain a constraint on the segmentation based on the resolution of a PDE. The study of the results allows us to observe the spatial information retained by the neural network on the region of interest and obtains competitive results on the binary segmentation. We illustrate the efficiency of this approach for medical image segmentation on a database of MRI brain images.

Fast Marching Energy CNN

Leveraging geodesic distances and the geometrical information they convey is key for many data-oriented applications in imaging. Geodesic distance computation has been used for long for image segmentation using Image based metrics. We introduce a new method by generating isotropic Riemannian metrics adapted to a problem using CNN and give as illustrations an example of application. We then apply this idea to the segmentation of brain tumours as unit balls for the geodesic distance computed with the metric potential output by a CNN, thus imposing geometrical and topological constraints on the output mask. We show that geodesic distance modules work well in machine learning frameworks and can be used to achieve state-of-the-art performances while ensuring geometrical and/or topological properties.

A model is worth tens of thousands of examples

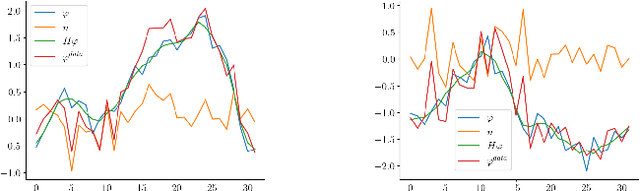
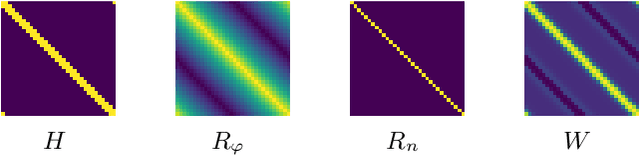
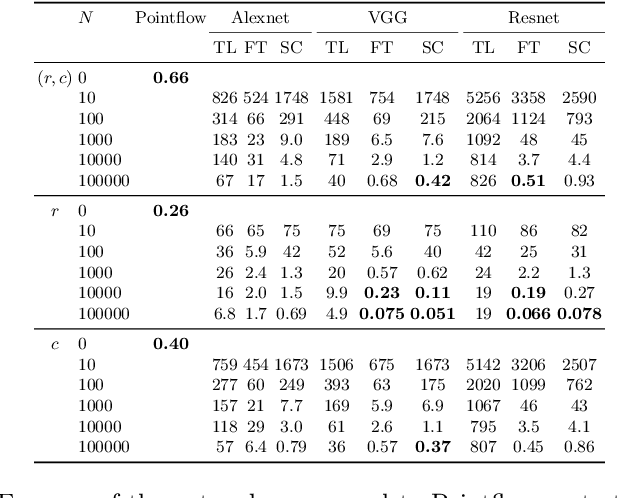
Traditional signal processing methods relying on mathematical data generation models have been cast aside in favour of deep neural networks, which require vast amounts of data. Since the theoretical sample complexity is nearly impossible to evaluate, these amounts of examples are usually estimated with crude rules of thumb. However, these rules only suggest when the networks should work, but do not relate to the traditional methods. In particular, an interesting question is: how much data is required for neural networks to be on par or outperform, if possible, the traditional model-based methods? In this work, we empirically investigate this question in two simple examples, where the data is generated according to precisely defined mathematical models, and where well-understood optimal or state-of-the-art mathematical data-agnostic solutions are known. A first problem is deconvolving one-dimensional Gaussian signals and a second one is estimating a circle's radius and location in random grayscale images of disks. By training various networks, either naive custom designed or well-established ones, with various amounts of training data, we find that networks require tens of thousands of examples in comparison to the traditional methods, whether the networks are trained from scratch or even with transfer-learning or finetuning.

Deformable Voxel Grids for Shape Comparisons

We present Deformable Voxel Grids (DVGs) for 3D shapes comparison and processing. It consists of a voxel grid which is deformed to approximate the silhouette of a shape, via energy-minimization. By interpreting the DVG as a local coordinates system, it provides a better embedding space than a regular voxel grid, since it is adapted to the geometry of the shape. It also allows to deform the shape by moving the control points of the DVG, in a similar manner to the Free Form Deformation, but with easier interpretability of the control points positions. After proposing a computation scheme of the energies compatible with meshes and pointclouds, we demonstrate the use of DVGs in a variety of applications: correspondences via cubification, style transfer, shape retrieval and PCA deformations. The first two require no learning and can be readily run on any shapes in a matter of minutes on modest hardware. As for the last two, they require to first optimize DVGs on a collection of shapes, which amounts to a pre-processing step. Then, determining PCA coordinates is straightforward and brings a few parameters to deform a shape.

Geodesic Models with Convexity Shape Prior

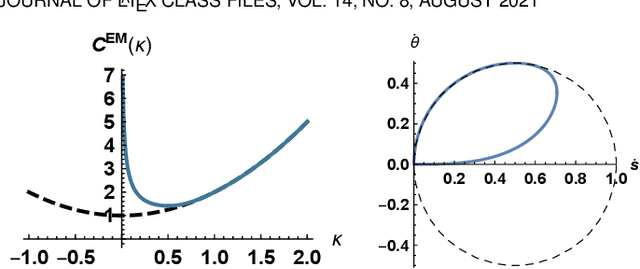
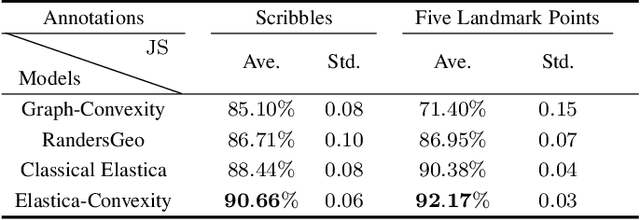
The minimal geodesic models based on the Eikonal equations are capable of finding suitable solutions in various image segmentation scenarios. Existing geodesic-based segmentation approaches usually exploit image features in conjunction with geometric regularization terms, such as Euclidean curve length or curvature-penalized length, for computing geodesic curves. In this paper, we take into account a more complicated problem: finding curvature-penalized geodesic paths with a convexity shape prior. We establish new geodesic models relying on the strategy of orientation-lifting, by which a planar curve can be mapped to an high-dimensional orientation-dependent space. The convexity shape prior serves as a constraint for the construction of local geodesic metrics encoding a particular curvature constraint. Then the geodesic distances and the corresponding closed geodesic paths in the orientation-lifted space can be efficiently computed through state-of-the-art Hamiltonian fast marching method. In addition, we apply the proposed geodesic models to the active contours, leading to efficient interactive image segmentation algorithms that preserve the advantages of convexity shape prior and curvature penalization.

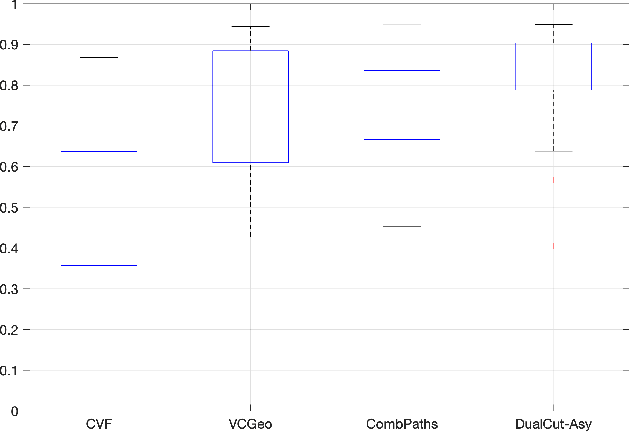
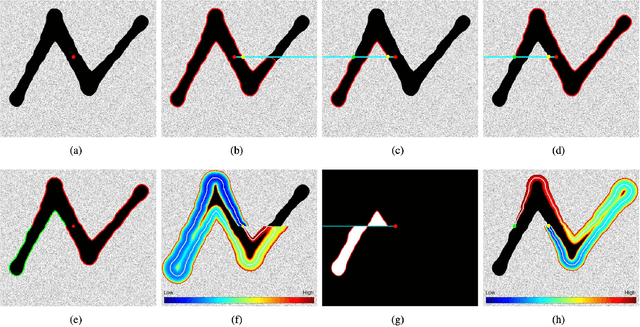
Geodesic Paths for Image Segmentation with Implicit Region-based Homogeneity Enhancement

Minimal paths are considered as a powerful and efficient tool for boundary detection and image segmentation due to its global optimality and well-established numerical solutions such as fast marching algorithm. In this paper, we introduce a flexible interactive image segmentation model based on the minimal geodesic framework in conjunction with region-based homogeneity enhancement. A key ingredient in our model is the construction of Finsler geodesic metrics, which are capable of integrating anisotropic and asymmetric edge features, region-based homogeneity and/or curvature regularization. This is done by exploiting an implicit method to incorporate the region-based homogeneity information to the metrics used. Moreover, we also introduce a way to build objective simple closed contours, each of which is treated as the concatenation of two disjoint open paths. Experimental results prove that the proposed model indeed outperforms state-of-the-art minimal paths-based image segmentation approaches.

A Generalized Asymmetric Dual-front Model for Active Contours and Image Segmentation

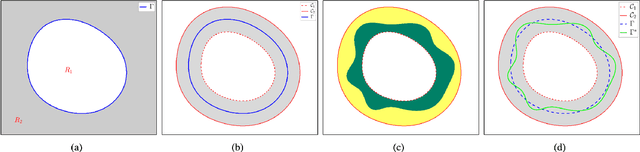
The geodesic distance-based dual-front curve evolution model is a powerful and efficient solution to the active contours and image segmentation issues. In its basic formulation, the dual-front model regards the meeting interfaces of two adjacent Voronoi regions as the evolving curves in the course of curve evolution. One of the most crucial ingredients for the construction of Voronoi regions or Voronoi diagram is the geodesic metrics and the corresponding geodesic distance. In this paper, we introduce a new type of geodesic metrics that encodes the edge-based anisotropy features, the region-based homogeneity penalization and asymmetric enhancement. In contrast to the original isotropic dual-front model, the use of the asymmetric enhancement can reduce the risk of shortcuts or leakage problems especially when the initial curves are far away from the target boundaries. Moreover, the proposed dual-front model can be applied for image segmentation in conjunction with various region-based homogeneity terms, whereas the original model only makes use of the piecewise constant case. The numerical experiments on both synthetic and real images show that the proposed model indeed achieves encouraging results.