Metric Convolutions: A Unifying Theory to Adaptive Convolutions

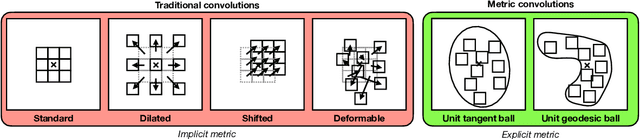
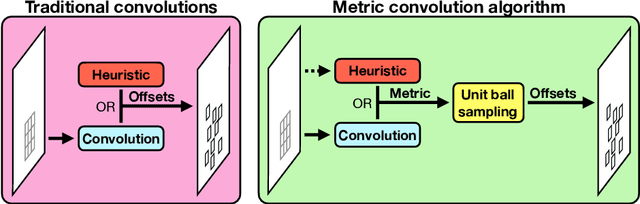
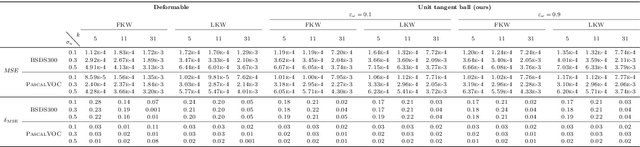
Standard convolutions are prevalent in image processing and deep learning, but their fixed kernel design limits adaptability. Several deformation strategies of the reference kernel grid have been proposed. Yet, they lack a unified theoretical framework. By returning to a metric perspective for images, now seen as two-dimensional manifolds equipped with notions of local and geodesic distances, either symmetric (Riemannian metrics) or not (Finsler metrics), we provide a unifying principle: the kernel positions are samples of unit balls of implicit metrics. With this new perspective, we also propose metric convolutions, a novel approach that samples unit balls from explicit signal-dependent metrics, providing interpretable operators with geometric regularisation. This framework, compatible with gradient-based optimisation, can directly replace existing convolutions applied to either input images or deep features of neural networks. Metric convolutions typically require fewer parameters and provide better generalisation. Our approach shows competitive performance in standard denoising and classification tasks.

Time, Travel, and Energy in the Uniform Dispersion Problem

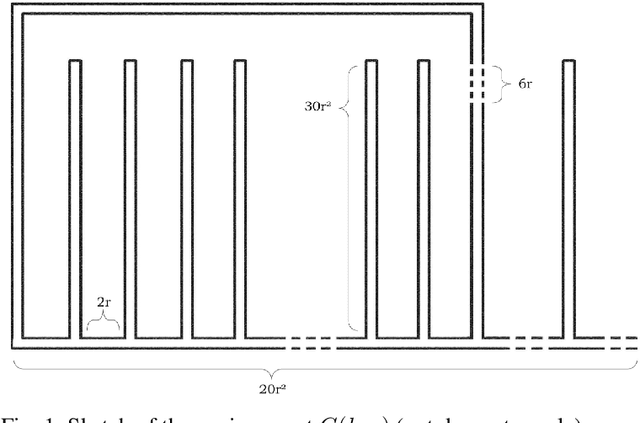
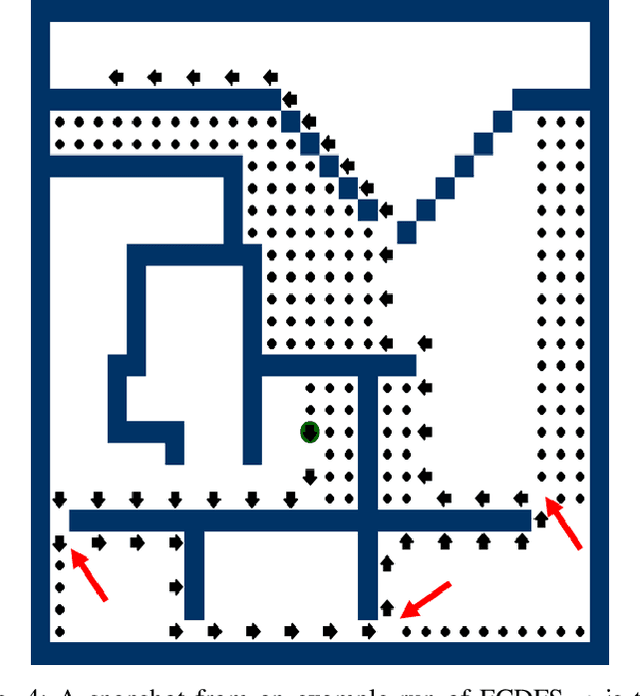
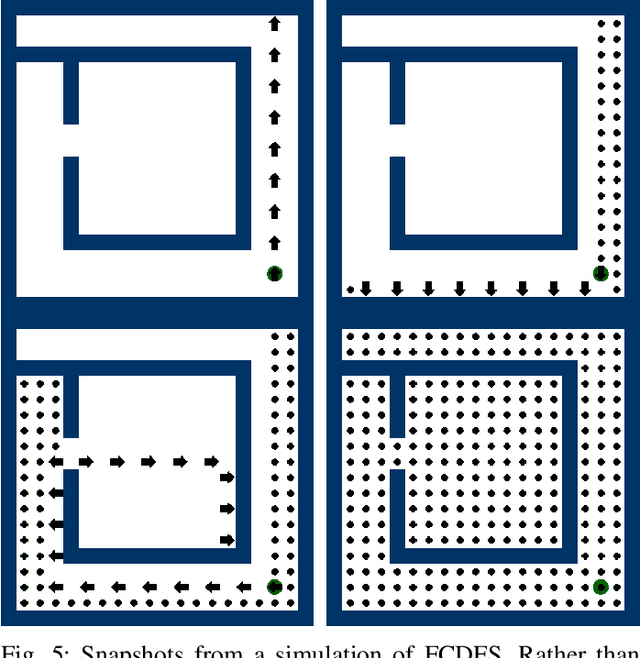
We investigate the algorithmic problem of uniformly dispersing a swarm of robots in an unknown, gridlike environment. In this setting, our goal is to comprehensively study the relationships between performance metrics and robot capabilities. We introduce a formal model comparing dispersion algorithms based on makespan, traveled distance, energy consumption, sensing, communication, and memory. Using this framework, we classify several uniform dispersion algorithms according to their capability requirements and performance. We prove that while makespan and travel can be minimized in all environments, energy cannot, as long as the swarm's sensing range is bounded. In contrast, we show that energy can be minimized even by simple, ``ant-like" robots in synchronous settings and asymptotically minimized in asynchronous settings, provided the environment is topologically simply connected. Our findings offer insights into fundamental limitations that arise when designing swarm robotics systems for exploring unknown environments, highlighting the impact of environment's topology on the feasibility of energy-efficient dispersion.

Patrolling Grids with a Bit of Memory

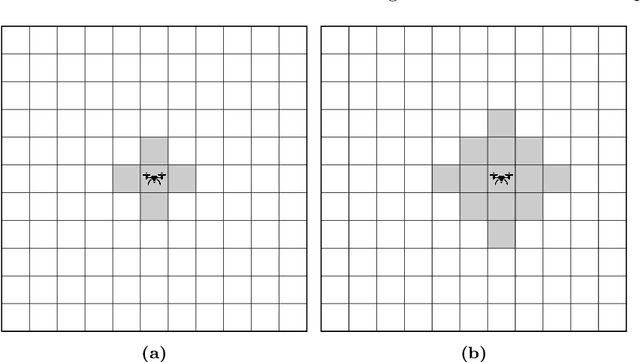
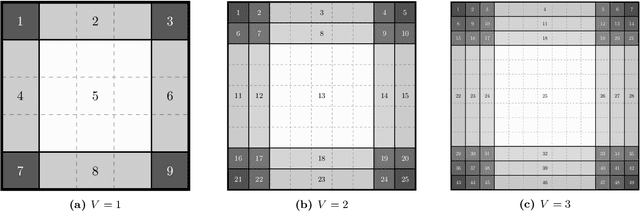
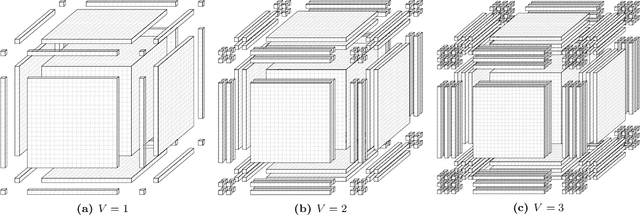
We study the following problem in elementary robotics: can a mobile agent with $b$ bits of memory, which is able to sense only locations at Manhattan distance $V$ or less from itself, patrol a $d$-dimensional grid graph? We show that it is impossible to patrol some grid graphs with $0$ bits of memory, regardless of $V$, and give an exact characterization of those grid graphs that can be patrolled with $0$ bits of memory and visibility range $V$. On the other hand, we show that, surprisingly, an algorithm exists using $1$ bit of memory and $V=1$ that patrols any $d$-dimensional grid graph.

A model is worth tens of thousands of examples

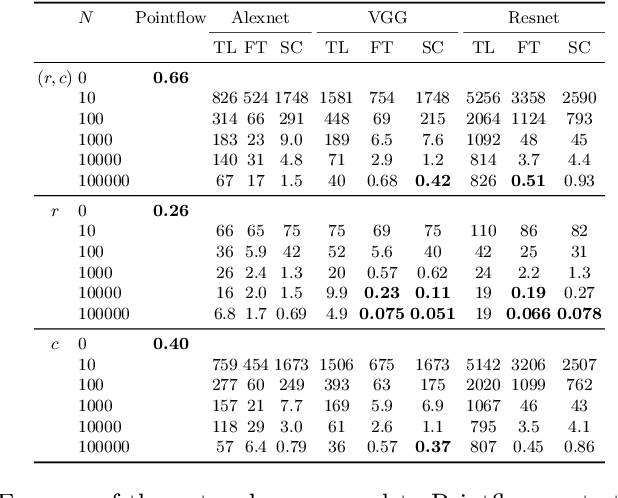
Traditional signal processing methods relying on mathematical data generation models have been cast aside in favour of deep neural networks, which require vast amounts of data. Since the theoretical sample complexity is nearly impossible to evaluate, these amounts of examples are usually estimated with crude rules of thumb. However, these rules only suggest when the networks should work, but do not relate to the traditional methods. In particular, an interesting question is: how much data is required for neural networks to be on par or outperform, if possible, the traditional model-based methods? In this work, we empirically investigate this question in two simple examples, where the data is generated according to precisely defined mathematical models, and where well-understood optimal or state-of-the-art mathematical data-agnostic solutions are known. A first problem is deconvolving one-dimensional Gaussian signals and a second one is estimating a circle's radius and location in random grayscale images of disks. By training various networks, either naive custom designed or well-established ones, with various amounts of training data, we find that networks require tens of thousands of examples in comparison to the traditional methods, whether the networks are trained from scratch or even with transfer-learning or finetuning.

From Compass and Ruler to Convolution and Nonlinearity: On the Surprising Difficulty of Understanding a Simple CNN Solving a Simple Geometric Estimation Task

Neural networks are omnipresent, but remain poorly understood. Their increasing complexity and use in critical systems raises the important challenge to full interpretability. We propose to address a simple well-posed learning problem: estimating the radius of a centred pulse in a one-dimensional signal or of a centred disk in two-dimensional images using a simple convolutional neural network. Surprisingly, understanding what trained networks have learned is difficult and, to some extent, counter-intuitive. However, an in-depth theoretical analysis in the one-dimensional case allows us to comprehend constraints due to the chosen architecture, the role of each filter and of the nonlinear activation function, and every single value taken by the weights of the model. Two fundamental concepts of neural networks arise: the importance of invariance and of the shape of the nonlinear activation functions.

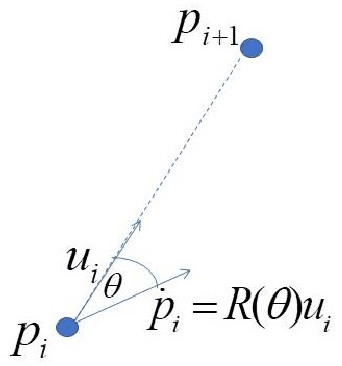
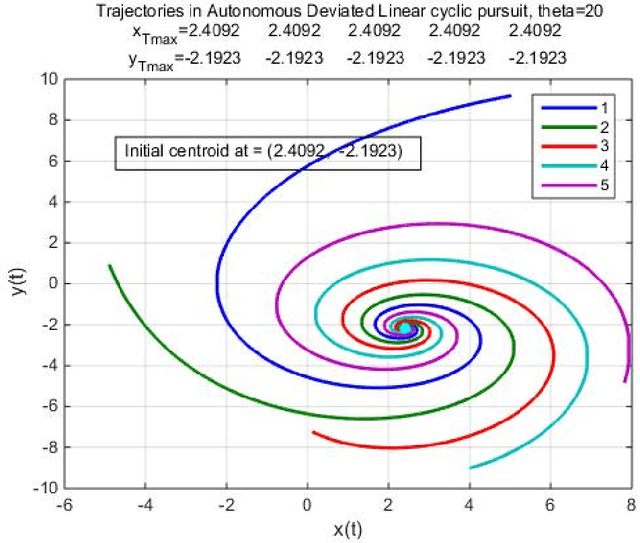
Broadcast Guidance of Agents in Deviated Linear Cyclic Pursuit

In this report we show the emergent behavior of a group of agents, ordered from 1 to n, performing deviated, linear, cyclic pursuit, in the presence of a broadcast guidance control. Each agent senses the relative position of its target, i.e. agent i senses the relative position of agent i+1. The broadcast control, a velocity signal, is detected by a random set of agents in the group. We assume the agents to be modeled as single integrators. We show that the emergent behavior of the group is determined by the deviation angle and by the set of agents detecting the guidance control.

Seeing Things in Random-Dot Videos

The human visual system correctly groups features and interprets videos displaying non persistent and noisy random-dot data induced by imaging natural dynamic scenes. Remarkably, this happens even if perception completely fails when the same information is presented frame by frame. We study this property of surprising dynamic perception with the first goal of proposing a new detection and spatio-temporal grouping algorithm for such signals when, per frame, the information on objects is both random and sparse. The striking similarity in performance of the algorithm to the perception by human observers, as witnessed by a series of psychophysical experiments that were performed, leads us to see in it a simple computational Gestalt model of human perception based on temporal integration and statistical tests of unlikeliness, the a contrario framework.

Probabilistic Pursuits on Graphs

We consider discrete dynamical systems of "ant-like" agents engaged in a sequence of pursuits on a graph environment. The agents emerge one by one at equal time intervals from a source vertex $s$ and pursue each other by greedily attempting to close the distance to their immediate predecessor, the agent that emerged just before them from $s$, until they arrive at the destination point $t$. Such pursuits have been investigated before in the continuous setting and in discrete time when the underlying environment is a regular grid. In both these settings the agents' walks provably converge to a shortest path from $s$ to $t$. Furthermore, assuming a certain natural probability distribution over the move choices of the agents on the grid (in case there are multiple shortest paths between an agent and its predecessor), the walks converge to the uniform distribution over all shortest paths from $s$ to $t$. We study the evolution of agent walks over a general finite graph environment $G$. Our model is a natural generalization of the pursuit rule proposed for the case of the grid. The main results are as follows. We show that "convergence" to the shortest paths in the sense of previous work extends to all pseudo-modular graphs (i.e. graphs in which every three pairwise intersecting disks have a nonempty intersection), and also to environments obtained by taking graph products, generalizing previous results in two different ways. We show that convergence to the shortest paths is also obtained by chordal graphs, and discuss some further positive and negative results for planar graphs. In the most general case, convergence to the shortest paths is not guaranteed, and the agents may get stuck on sets of recurrent, non-optimal walks from $s$ to $t$. However, we show that the limiting distributions of the agents' walks will always be uniform distributions over some set of walks of equal length.

Real-Time Depth Refinement for Specular Objects

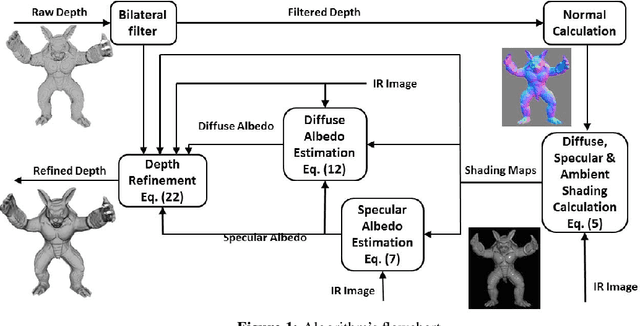
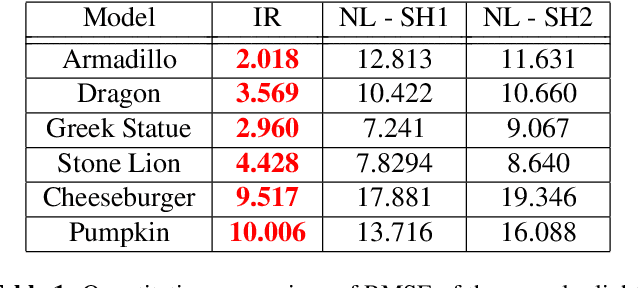
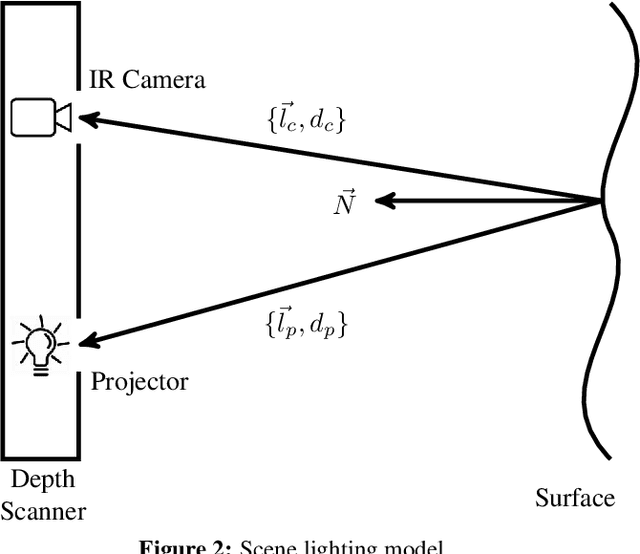
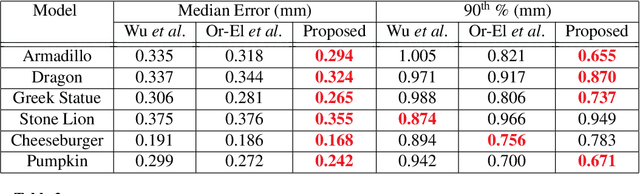
The introduction of consumer RGB-D scanners set off a major boost in 3D computer vision research. Yet, the precision of existing depth scanners is not accurate enough to recover fine details of a scanned object. While modern shading based depth refinement methods have been proven to work well with Lambertian objects, they break down in the presence of specularities. We present a novel shape from shading framework that addresses this issue and enhances both diffuse and specular objects' depth profiles. We take advantage of the built-in monochromatic IR projector and IR images of the RGB-D scanners and present a lighting model that accounts for the specular regions in the input image. Using this model, we reconstruct the depth map in real-time. Both quantitative tests and visual evaluations prove that the proposed method produces state of the art depth reconstruction results.

Postprocessing of Compressed Images via Sequential Denoising

In this work we propose a novel postprocessing technique for compression-artifact reduction. Our approach is based on posing this task as an inverse problem, with a regularization that leverages on existing state-of-the-art image denoising algorithms. We rely on the recently proposed Plug-and-Play Prior framework, suggesting the solution of general inverse problems via Alternating Direction Method of Multipliers (ADMM), leading to a sequence of Gaussian denoising steps. A key feature in our scheme is a linearization of the compression-decompression process, so as to get a formulation that can be optimized. In addition, we supply a thorough analysis of this linear approximation for several basic compression procedures. The proposed method is suitable for diverse compression techniques that rely on transform coding. Specifically, we demonstrate impressive gains in image quality for several leading compression methods - JPEG, JPEG2000, and HEVC.