Wormhole Loss for Partial Shape Matching

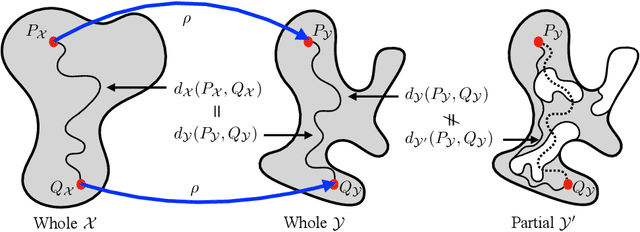
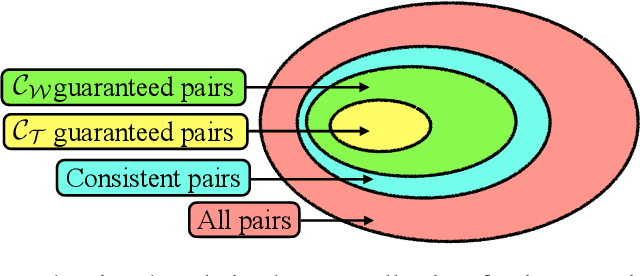
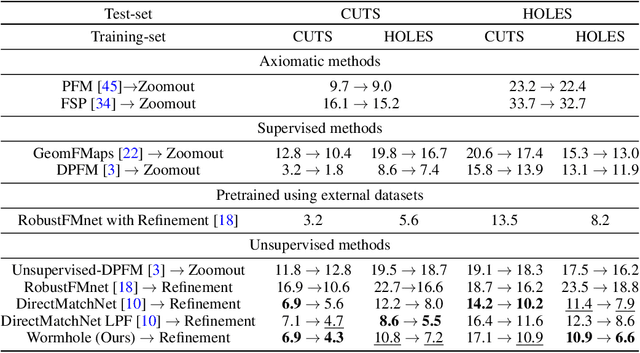
When matching parts of a surface to its whole, a fundamental question arises: Which points should be included in the matching process? The issue is intensified when using isometry to measure similarity, as it requires the validation of whether distances measured between pairs of surface points should influence the matching process. The approach we propose treats surfaces as manifolds equipped with geodesic distances, and addresses the partial shape matching challenge by introducing a novel criterion to meticulously search for consistent distances between pairs of points. The new criterion explores the relation between intrinsic geodesic distances between the points, geodesic distances between the points and surface boundaries, and extrinsic distances between boundary points measured in the embedding space. It is shown to be less restrictive compared to previous measures and achieves state-of-the-art results when used as a loss function in training networks for partial shape matching.

Metric Convolutions: A Unifying Theory to Adaptive Convolutions

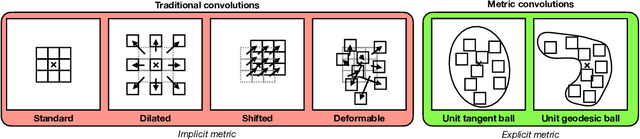
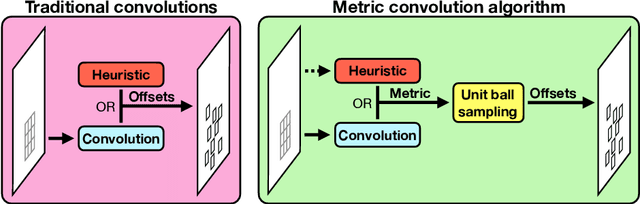
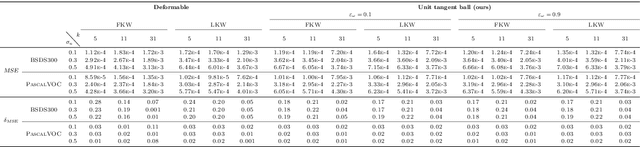
Standard convolutions are prevalent in image processing and deep learning, but their fixed kernel design limits adaptability. Several deformation strategies of the reference kernel grid have been proposed. Yet, they lack a unified theoretical framework. By returning to a metric perspective for images, now seen as two-dimensional manifolds equipped with notions of local and geodesic distances, either symmetric (Riemannian metrics) or not (Finsler metrics), we provide a unifying principle: the kernel positions are samples of unit balls of implicit metrics. With this new perspective, we also propose metric convolutions, a novel approach that samples unit balls from explicit signal-dependent metrics, providing interpretable operators with geometric regularisation. This framework, compatible with gradient-based optimisation, can directly replace existing convolutions applied to either input images or deep features of neural networks. Metric convolutions typically require fewer parameters and provide better generalisation. Our approach shows competitive performance in standard denoising and classification tasks.

Finsler-Laplace-Beltrami Operators with Application to Shape Analysis

The Laplace-Beltrami operator (LBO) emerges from studying manifolds equipped with a Riemannian metric. It is often called the Swiss army knife of geometry processing as it allows to capture intrinsic shape information and gives rise to heat diffusion, geodesic distances, and a multitude of shape descriptors. It also plays a central role in geometric deep learning. In this work, we explore Finsler manifolds as a generalization of Riemannian manifolds. We revisit the Finsler heat equation and derive a Finsler heat kernel and a Finsler-Laplace-Beltrami Operator (FLBO): a novel theoretically justified anisotropic Laplace-Beltrami operator (ALBO). In experimental evaluations we demonstrate that the proposed FLBO is a valuable alternative to the traditional Riemannian-based LBO and ALBOs for spatial filtering and shape correspondence estimation. We hope that the proposed Finsler heat kernel and the FLBO will inspire further exploration of Finsler geometry in the computer vision community.

On Partial Shape Correspondence and Functional Maps

While dealing with matching shapes to their parts, we often utilize an instrument known as functional maps. The idea is to translate the shape matching problem into ``convenient'' spaces by which matching is performed algebraically by solving a least squares problem. Here, we argue that such formulations, though popular in this field, introduce errors in the estimated match when partiality is invoked. Such errors are unavoidable even when considering advanced feature extraction networks, and they can be shown to escalate with increasing degrees of shape partiality, adversely affecting the learning capability of such systems. To circumvent these limitations, we propose a novel approach for partial shape matching. Our study of functional maps led us to a novel method that establishes direct correspondence between partial and full shapes through feature matching bypassing the need for functional map intermediate spaces. The Gromov distance between metric spaces leads to the construction of the first part of our loss functions. For regularization we use two options: a term based on the area preserving property of the mapping, and a relaxed version of it without the need to compute a functional map. The proposed approach shows superior performance on the SHREC'16 dataset, outperforming existing unsupervised methods for partial shape matching. In particular, it achieves state-of-the-art result on the SHREC'16 HOLES benchmark, superior also compared to supervised methods.

A model is worth tens of thousands of examples

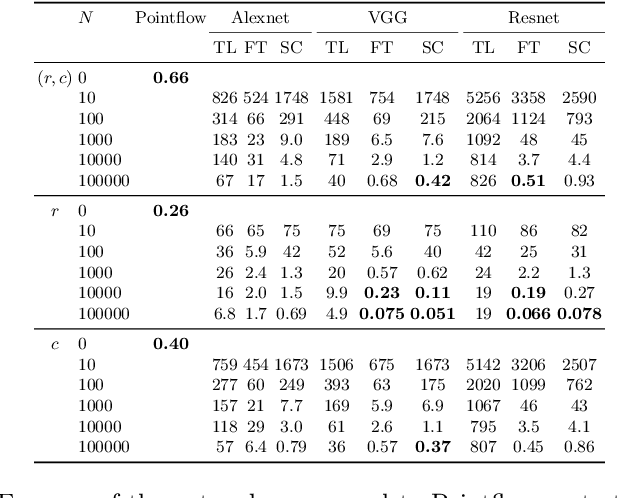
Traditional signal processing methods relying on mathematical data generation models have been cast aside in favour of deep neural networks, which require vast amounts of data. Since the theoretical sample complexity is nearly impossible to evaluate, these amounts of examples are usually estimated with crude rules of thumb. However, these rules only suggest when the networks should work, but do not relate to the traditional methods. In particular, an interesting question is: how much data is required for neural networks to be on par or outperform, if possible, the traditional model-based methods? In this work, we empirically investigate this question in two simple examples, where the data is generated according to precisely defined mathematical models, and where well-understood optimal or state-of-the-art mathematical data-agnostic solutions are known. A first problem is deconvolving one-dimensional Gaussian signals and a second one is estimating a circle's radius and location in random grayscale images of disks. By training various networks, either naive custom designed or well-established ones, with various amounts of training data, we find that networks require tens of thousands of examples in comparison to the traditional methods, whether the networks are trained from scratch or even with transfer-learning or finetuning.

From Compass and Ruler to Convolution and Nonlinearity: On the Surprising Difficulty of Understanding a Simple CNN Solving a Simple Geometric Estimation Task

Neural networks are omnipresent, but remain poorly understood. Their increasing complexity and use in critical systems raises the important challenge to full interpretability. We propose to address a simple well-posed learning problem: estimating the radius of a centred pulse in a one-dimensional signal or of a centred disk in two-dimensional images using a simple convolutional neural network. Surprisingly, understanding what trained networks have learned is difficult and, to some extent, counter-intuitive. However, an in-depth theoretical analysis in the one-dimensional case allows us to comprehend constraints due to the chosen architecture, the role of each filter and of the nonlinear activation function, and every single value taken by the weights of the model. Two fundamental concepts of neural networks arise: the importance of invariance and of the shape of the nonlinear activation functions.

Seeing Things in Random-Dot Videos

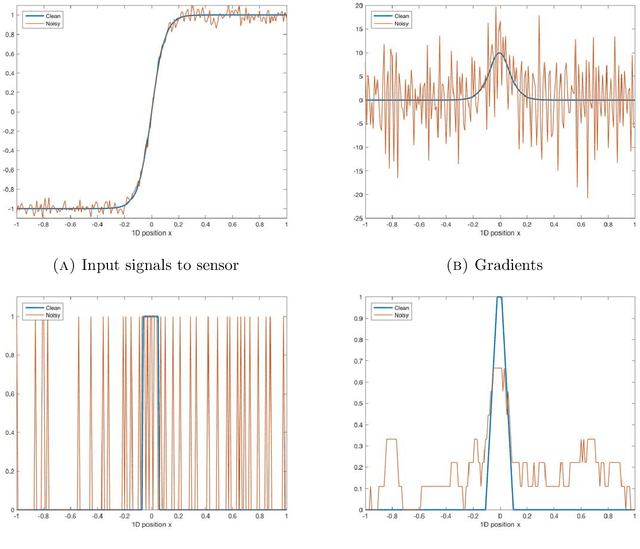
The human visual system correctly groups features and interprets videos displaying non persistent and noisy random-dot data induced by imaging natural dynamic scenes. Remarkably, this happens even if perception completely fails when the same information is presented frame by frame. We study this property of surprising dynamic perception with the first goal of proposing a new detection and spatio-temporal grouping algorithm for such signals when, per frame, the information on objects is both random and sparse. The striking similarity in performance of the algorithm to the perception by human observers, as witnessed by a series of psychophysical experiments that were performed, leads us to see in it a simple computational Gestalt model of human perception based on temporal integration and statistical tests of unlikeliness, the a contrario framework.