Wormhole Loss for Partial Shape Matching

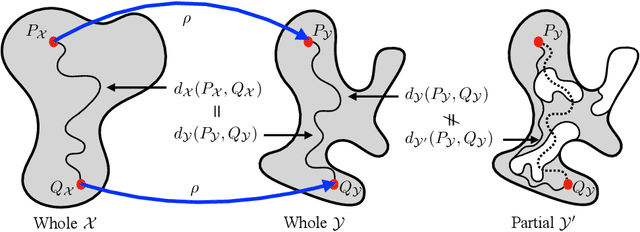
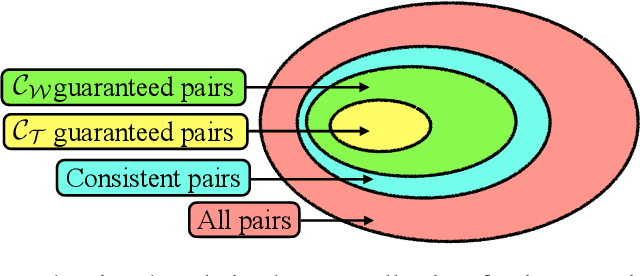
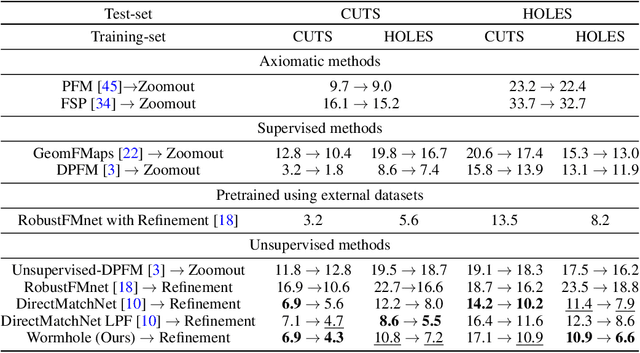
When matching parts of a surface to its whole, a fundamental question arises: Which points should be included in the matching process? The issue is intensified when using isometry to measure similarity, as it requires the validation of whether distances measured between pairs of surface points should influence the matching process. The approach we propose treats surfaces as manifolds equipped with geodesic distances, and addresses the partial shape matching challenge by introducing a novel criterion to meticulously search for consistent distances between pairs of points. The new criterion explores the relation between intrinsic geodesic distances between the points, geodesic distances between the points and surface boundaries, and extrinsic distances between boundary points measured in the embedding space. It is shown to be less restrictive compared to previous measures and achieves state-of-the-art results when used as a loss function in training networks for partial shape matching.

Surface Reconstruction from Gaussian Splatting via Novel Stereo Views

The Gaussian splatting for radiance field rendering method has recently emerged as an efficient approach for accurate scene representation. It optimizes the location, size, color, and shape of a cloud of 3D Gaussian elements to visually match, after projection, or splatting, a set of given images taken from various viewing directions. And yet, despite the proximity of Gaussian elements to the shape boundaries, direct surface reconstruction of objects in the scene is a challenge. We propose a novel approach for surface reconstruction from Gaussian splatting models. Rather than relying on the Gaussian elements' locations as a prior for surface reconstruction, we leverage the superior novel-view synthesis capabilities of 3DGS. To that end, we use the Gaussian splatting model to render pairs of stereo-calibrated novel views from which we extract depth profiles using a stereo matching method. We then combine the extracted RGB-D images into a geometrically consistent surface. The resulting reconstruction is more accurate and shows finer details when compared to other methods for surface reconstruction from Gaussian splatting models, while requiring significantly less compute time compared to other surface reconstruction methods. We performed extensive testing of the proposed method on in-the-wild scenes, taken by a smartphone, showcasing its superior reconstruction abilities. Additionally, we tested the proposed method on the Tanks and Temples benchmark, and it has surpassed the current leading method for surface reconstruction from Gaussian splatting models. Project page: https://gs2mesh.github.io/.

On Partial Shape Correspondence and Functional Maps

While dealing with matching shapes to their parts, we often utilize an instrument known as functional maps. The idea is to translate the shape matching problem into ``convenient'' spaces by which matching is performed algebraically by solving a least squares problem. Here, we argue that such formulations, though popular in this field, introduce errors in the estimated match when partiality is invoked. Such errors are unavoidable even when considering advanced feature extraction networks, and they can be shown to escalate with increasing degrees of shape partiality, adversely affecting the learning capability of such systems. To circumvent these limitations, we propose a novel approach for partial shape matching. Our study of functional maps led us to a novel method that establishes direct correspondence between partial and full shapes through feature matching bypassing the need for functional map intermediate spaces. The Gromov distance between metric spaces leads to the construction of the first part of our loss functions. For regularization we use two options: a term based on the area preserving property of the mapping, and a relaxed version of it without the need to compute a functional map. The proposed approach shows superior performance on the SHREC'16 dataset, outperforming existing unsupervised methods for partial shape matching. In particular, it achieves state-of-the-art result on the SHREC'16 HOLES benchmark, superior also compared to supervised methods.

Partial Shape Similarity via Alignment of Multi-Metric Hamiltonian Spectra

Evaluating the similarity of non-rigid shapes with significant partiality is a fundamental task in numerous computer vision applications. Here, we propose a novel axiomatic method to match similar regions across shapes. Matching similar regions is formulated as the alignment of the spectra of operators closely related to the Laplace-Beltrami operator (LBO). The main novelty of the proposed approach is the consideration of differential operators defined on a manifold with multiple metrics. The choice of a metric relates to fundamental shape properties while considering the same manifold under different metrics can thus be viewed as analyzing the underlying manifold from different perspectives. Specifically, we examine the scale-invariant metric and the corresponding scale-invariant Laplace-Beltrami operator (SI-LBO) along with the regular metric and the regular LBO. We demonstrate that the scale-invariant metric emphasizes the locations of important semantic features in articulated shapes. A truncated spectrum of the SI-LBO consequently better captures locally curved regions and complements the global information encapsulated in the truncated spectrum of the regular LBO. We show that matching these dual spectra outperforms competing axiomatic frameworks when tested on standard benchmarks. We introduced a new dataset and compare the proposed method with the state-of-the-art learning based approach in a cross-database configuration. Specifically, we show that, when trained on one data set and tested on another, the proposed axiomatic approach which does not involve training, outperforms the deep learning alternative.

Depth Refinement for Improved Stereo Reconstruction

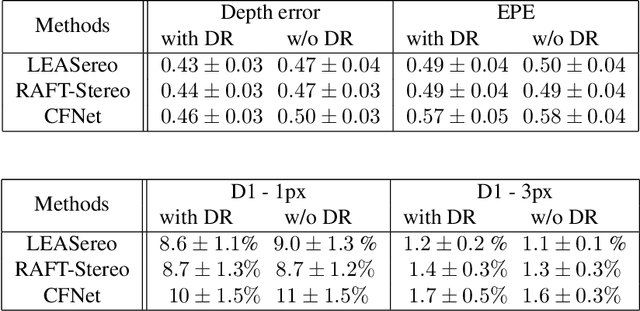
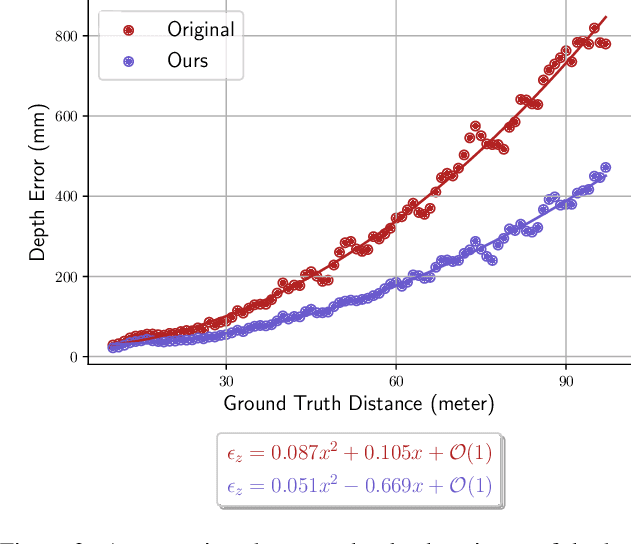
Depth estimation is a cornerstone of a vast number of applications requiring 3D assessment of the environment, such as robotics, augmented reality, and autonomous driving to name a few. One prominent technique for depth estimation is stereo matching which has several advantages: it is considered more accessible than other depth-sensing technologies, can produce dense depth estimates in real-time, and has benefited greatly from the advances of deep learning in recent years. However, current techniques for depth estimation from stereoscopic images still suffer from a built-in drawback. To reconstruct depth, a stereo matching algorithm first estimates the disparity map between the left and right images before applying a geometric triangulation. A simple analysis reveals that the depth error is quadratically proportional to the object's distance. Therefore, constant disparity errors are translated to large depth errors for objects far from the camera. To mitigate this quadratic relation, we propose a simple but effective method that uses a refinement network for depth estimation. We show analytical and empirical results suggesting that the proposed learning procedure reduces this quadratic relation. We evaluate the proposed refinement procedure on well-known benchmarks and datasets, like Sceneflow and KITTI datasets, and demonstrate significant improvements in the depth accuracy metric.

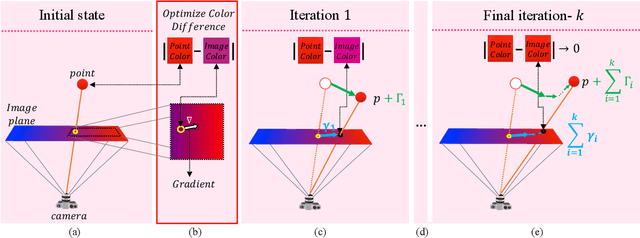
Colored Point Cloud to Image Alignment

Recognition and segmentation of objects in images enjoy the wealth of large volume of well annotated data. At the other end, when dealing with the reconstruction of geometric structures of objects from images, there is a limited amount of accurate data available for supervised learning. One type of such geometric data with insufficient amount required for deep learning is real world accurate RGB-D images. The lack of accurate RGB-D datasets is one of the obstacles in the evolution of geometric scene reconstructions from images. One solution to creating such a dataset is to capture RGB images while simultaneously using an accurate depth scanning device that assigns a depth value to each pixel. A major challenge in acquiring such ground truth data is the accurate alignment between the RGB images and the measured depth and color profiles. We introduce a differential optimization method that aligns a colored point cloud to a given color image via iterative geometric and color matching. The proposed method enables the construction of RGB-D datasets for specific camera systems. In the suggested framework, the optimization minimizes the difference between the colors of the image pixels and the corresponding colors of the projected points to the camera plane. We assume that the colors produced by the geometric scanner camera and the color camera sensor are different and thus are characterized by different chromatic acquisition properties. We align the different color spaces while compensating for their corresponding color appearance. Under this setup, we find the transformation between the camera image and the point cloud colors by iterating between matching the relative location of the point cloud and matching colors. The successful alignments produced by the proposed method are demonstrated on both synthetic data with quantitative evaluation and real world scenes with qualitative results.