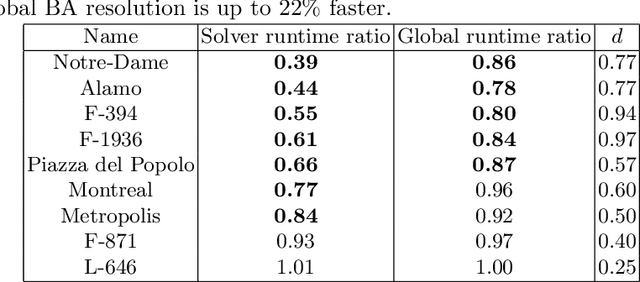
Power Variable Projection for Initialization-Free Large-Scale Bundle Adjustment

Initialization-free bundle adjustment (BA) remains largely uncharted. While Levenberg-Marquardt algorithm is the golden method to solve the BA problem, it generally relies on a good initialization. In contrast, the under-explored Variable Projection algorithm (VarPro) exhibits a wide convergence basin even without initialization. Coupled with object space error formulation, recent works have shown its ability to solve (small-scale) initialization-free bundle adjustment problem. We introduce Power Variable Projection (PoVar), extending a recent inverse expansion method based on power series. Importantly, we link the power series expansion to Riemannian manifold optimization. This projective framework is crucial to solve large-scale bundle adjustment problem without initialization. Using the real-world BAL dataset, we experimentally demonstrate that our solver achieves state-of-the-art results in terms of speed and accuracy. In particular, our work is the first, to our knowledge, that addresses the scalability of BA without initialization and opens new venues for initialization-free Structure-from-Motion.

Flattening the Parent Bias: Hierarchical Semantic Segmentation in the Poincaré Ball

Hierarchy is a natural representation of semantic taxonomies, including the ones routinely used in image segmentation. Indeed, recent work on semantic segmentation reports improved accuracy from supervised training leveraging hierarchical label structures. Encouraged by these results, we revisit the fundamental assumptions behind that work. We postulate and then empirically verify that the reasons for the observed improvement in segmentation accuracy may be entirely unrelated to the use of the semantic hierarchy. To demonstrate this, we design a range of cross-domain experiments with a representative hierarchical approach. We find that on the new testing domains, a flat (non-hierarchical) segmentation network, in which the parents are inferred from the children, has superior segmentation accuracy to the hierarchical approach across the board. Complementing these findings and inspired by the intrinsic properties of hyperbolic spaces, we study a more principled approach to hierarchical segmentation using the Poincar\'e ball model. The hyperbolic representation largely outperforms the previous (Euclidean) hierarchical approach as well and is on par with our flat Euclidean baseline in terms of segmentation accuracy. However, it additionally exhibits surprisingly strong calibration quality of the parent nodes in the semantic hierarchy, especially on the more challenging domains. Our combined analysis suggests that the established practice of hierarchical segmentation may be limited to in-domain settings, whereas flat classifiers generalize substantially better, especially if they are modeled in the hyperbolic space.

Finsler-Laplace-Beltrami Operators with Application to Shape Analysis

The Laplace-Beltrami operator (LBO) emerges from studying manifolds equipped with a Riemannian metric. It is often called the Swiss army knife of geometry processing as it allows to capture intrinsic shape information and gives rise to heat diffusion, geodesic distances, and a multitude of shape descriptors. It also plays a central role in geometric deep learning. In this work, we explore Finsler manifolds as a generalization of Riemannian manifolds. We revisit the Finsler heat equation and derive a Finsler heat kernel and a Finsler-Laplace-Beltrami Operator (FLBO): a novel theoretically justified anisotropic Laplace-Beltrami operator (ALBO). In experimental evaluations we demonstrate that the proposed FLBO is a valuable alternative to the traditional Riemannian-based LBO and ALBOs for spatial filtering and shape correspondence estimation. We hope that the proposed Finsler heat kernel and the FLBO will inspire further exploration of Finsler geometry in the computer vision community.

Reducing Nearest Neighbor Training Sets Optimally and Exactly

In nearest-neighbor classification, a training set $P$ of points in $\mathbb{R}^d$ with given classification is used to classify every point in $\mathbb{R}^d$: Every point gets the same classification as its nearest neighbor in $P$. Recently, Eppstein [SOSA'22] developed an algorithm to detect the relevant training points, those points $p\in P$, such that $P$ and $P\setminus\{p\}$ induce different classifications. We investigate the problem of finding the minimum cardinality reduced training set $P'\subseteq P$ such that $P$ and $P'$ induce the same classification. We show that the set of relevant points is such a minimum cardinality reduced training set if $P$ is in general position. Furthermore, we show that finding a minimum cardinality reduced training set for possibly degenerate $P$ is in P for $d=1$, and NP-complete for $d\geq 2$.

Power Bundle Adjustment for Large-Scale 3D Reconstruction

We present the design and the implementation of a new expansion type algorithm to solve large-scale bundle adjustment problems. Our approach -- called Power Bundle Adjustment -- is based on the power series expansion of the inverse Schur complement. This initiates a new family of solvers that we call inverse expansion methods. We show with the real-world BAL dataset that the proposed solver challenges the traditional direct and iterative methods. The solution of the normal equation is significantly accelerated, even for reaching a very high accuracy. Last but not least, our solver can also complement a recently presented distributed bundle adjustment framework. We demonstrate that employing the proposed Power Bundle Adjustment as a sub-problem solver greatly improves speed and accuracy of the distributed optimization.

Training Fully Connected Neural Networks is $\exists\mathbb{R}$-Complete

We consider the algorithmic problem of finding the optimal weights and biases for a two-layer fully connected neural network to fit a given set of data points. This problem is known as empirical risk minimization in the machine learning community. We show that the problem is $\exists\mathbb{R}$-complete. This complexity class can be defined as the set of algorithmic problems that are polynomial-time equivalent to finding real roots of a polynomial with integer coefficients. Our results hold even if the following restrictions are all added simultaneously. $\bullet$ There are exactly two output neurons. $\bullet$ There are exactly two input neurons. $\bullet$ The data has only 13 different labels. $\bullet$ The number of hidden neurons is a constant fraction of the number of data points. $\bullet$ The target training error is zero. $\bullet$ The ReLU activation function is used. This shows that even very simple networks are difficult to train. The result offers an explanation (though far from a complete understanding) on why only gradient descent is widely successful in training neural networks in practice. We generalize a recent result by Abrahamsen, Kleist and Miltzow [NeurIPS 2021]. This result falls into a recent line of research that tries to unveil that a series of central algorithmic problems from widely different areas of computer science and mathematics are $\exists\mathbb{R}$-complete: This includes the art gallery problem [JACM/STOC 2018], geometric packing [FOCS 2020], covering polygons with convex polygons [FOCS 2021], and continuous constraint satisfaction problems [FOCS 2021].

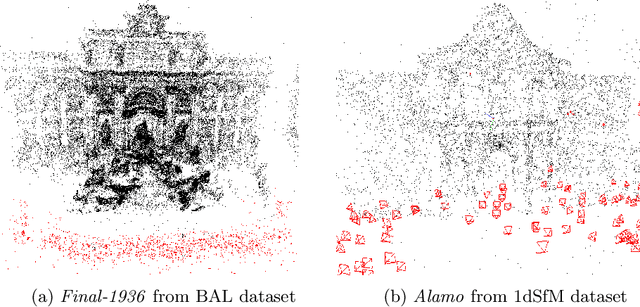
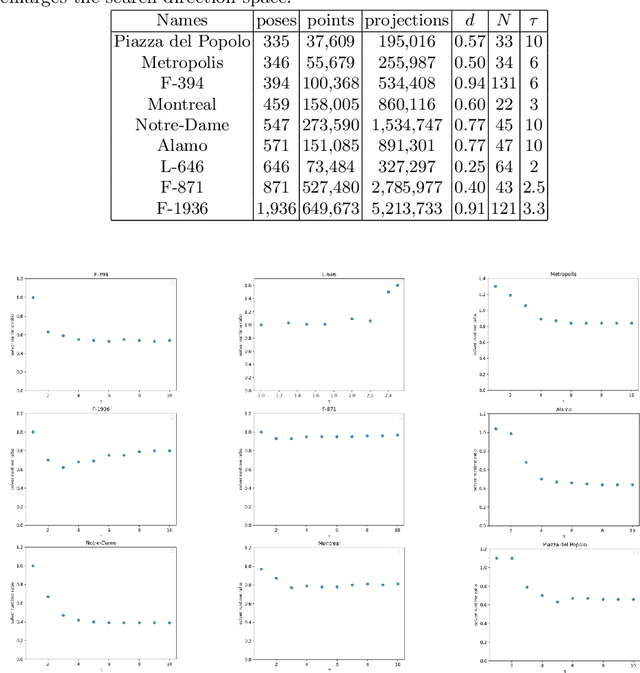
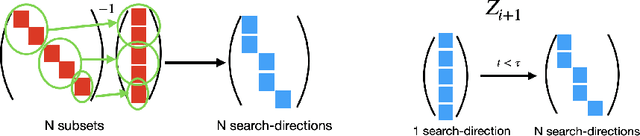
Multidirectional Conjugate Gradients for Scalable Bundle Adjustment

We revisit the problem of large-scale bundle adjustment and propose a technique called Multidirectional Conjugate Gradients that accelerates the solution of the normal equation by up to 61%. The key idea is that we enlarge the search space of classical preconditioned conjugate gradients to include multiple search directions. As a consequence, the resulting algorithm requires fewer iterations, leading to a significant speedup of large-scale reconstruction, in particular for denser problems where traditional approaches notoriously struggle. We provide a number of experimental ablation studies revealing the robustness to variations in the hyper-parameters and the speedup as a function of problem density.

Algorithmic Programming Language Identification

Motivated by the amount of code that goes unidentified on the web, we introduce a practical method for algorithmically identifying the programming language of source code. Our work is based on supervised learning and intelligent statistical features. We also explored, but abandoned, a grammatical approach. In testing, our implementation greatly outperforms that of an existing tool that relies on a Bayesian classifier. Code is written in Python and available under an MIT license.