Training Fully Connected Neural Networks is $\exists\mathbb{R}$-Complete

We consider the algorithmic problem of finding the optimal weights and biases for a two-layer fully connected neural network to fit a given set of data points. This problem is known as empirical risk minimization in the machine learning community. We show that the problem is $\exists\mathbb{R}$-complete. This complexity class can be defined as the set of algorithmic problems that are polynomial-time equivalent to finding real roots of a polynomial with integer coefficients. Our results hold even if the following restrictions are all added simultaneously. $\bullet$ There are exactly two output neurons. $\bullet$ There are exactly two input neurons. $\bullet$ The data has only 13 different labels. $\bullet$ The number of hidden neurons is a constant fraction of the number of data points. $\bullet$ The target training error is zero. $\bullet$ The ReLU activation function is used. This shows that even very simple networks are difficult to train. The result offers an explanation (though far from a complete understanding) on why only gradient descent is widely successful in training neural networks in practice. We generalize a recent result by Abrahamsen, Kleist and Miltzow [NeurIPS 2021]. This result falls into a recent line of research that tries to unveil that a series of central algorithmic problems from widely different areas of computer science and mathematics are $\exists\mathbb{R}$-complete: This includes the art gallery problem [JACM/STOC 2018], geometric packing [FOCS 2020], covering polygons with convex polygons [FOCS 2021], and continuous constraint satisfaction problems [FOCS 2021].

On Classifying Continuous Constraint Satisfaction problems

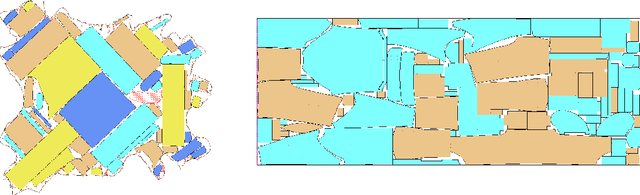
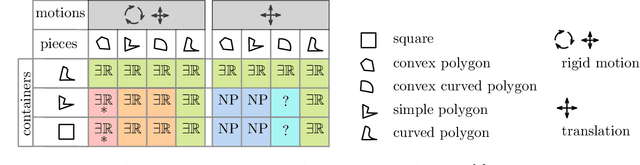
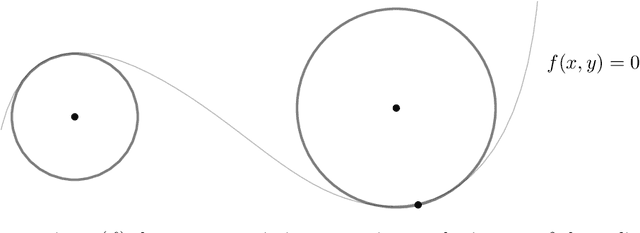
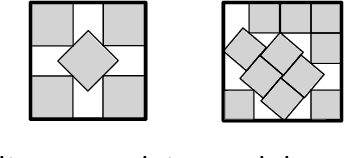
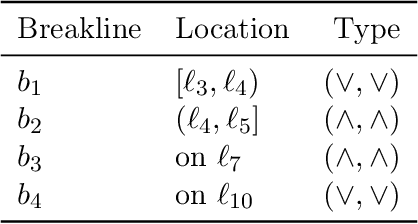
A continuous constraint satisfaction problem (CCSP) is a constraint satisfaction problem (CSP) with a domain $U \subset \mathbb{R}$. We engage in a systematic study to classify CCSPs that are complete of the Existential Theory of the Reals, i.e., ER-complete. To define this class, we first consider the problem ETR, which also stands for Existential Theory of the Reals. In an instance of this problem we are given some sentence of the form $\exists x_1, \ldots, x_n \in \mathbb{R} : \Phi(x_1, \ldots, x_n)$, where $\Phi$ is a well-formed quantifier-free formula consisting of the symbols $\{0, 1, +, \cdot, \geq, >, \wedge, \vee, \neg\}$, the goal is to check whether this sentence is true. Now the class ER is the family of all problems that admit a polynomial-time reduction to ETR. It is known that NP $\subseteq$ ER $\subseteq$ PSPACE. We restrict our attention on CCSPs with addition constraints ($x + y = z$) and some other mild technical condition. Previously, it was shown that multiplication constraints ($x \cdot y = z$), squaring constraints ($x^2 = y$), or inversion constraints ($x\cdot y = 1$) are sufficient to establish ER-completeness. We extend this in the strongest possible sense for equality constraints as follows. We show that CCSPs (with addition constraints and some other mild technical condition) that have any one well-behaved curved equality constraint ($f(x,y) = 0$) are ER-complete. We further extend our results to inequality constraints. We show that any well-behaved convexly curved and any well-behaved concavely curved inequality constraint ($f(x,y) \geq 0$ and $g(x,y) \geq 0$) imply ER-completeness on the class of such CCSPs. We apply our findings to geometric packing and answer an open question by Abrahamsen et al. [FOCS 2020]. Namely, we establish ER-completeness of packing convex pieces into a square container under rotations and translations.

Training Neural Networks is ER-complete

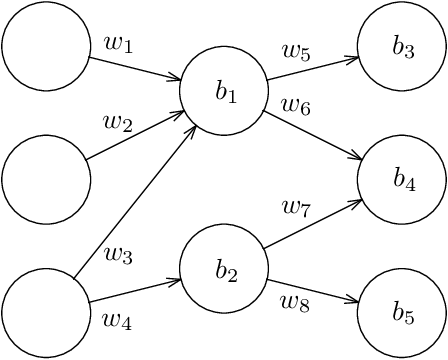
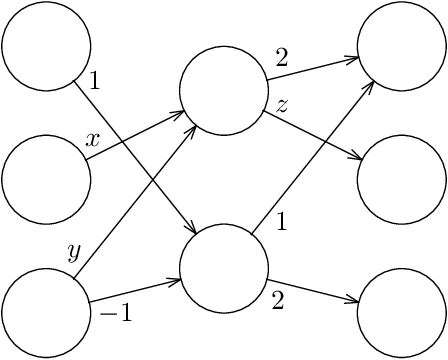
Given a neural network, training data, and a threshold, it was known that it is NP-hard to find weights for the neural network such that the total error is below the threshold. We determine the algorithmic complexity of this fundamental problem precisely, by showing that it is ER-complete. This means that the problem is equivalent, up to polynomial-time reductions, to deciding whether a system of polynomial equations and inequalities with integer coefficients and real unknowns has a solution. If, as widely expected, ER is strictly larger than NP, our work implies that the problem of training neural networks is not even in NP.