Training Neural Networks is ER-complete
Paper and Code
Feb 19, 2021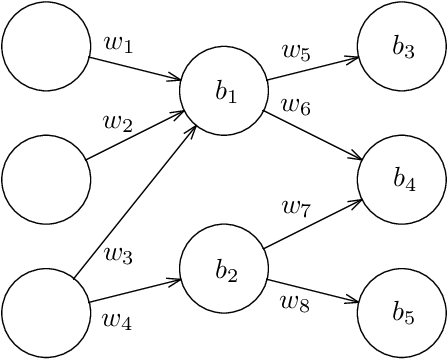
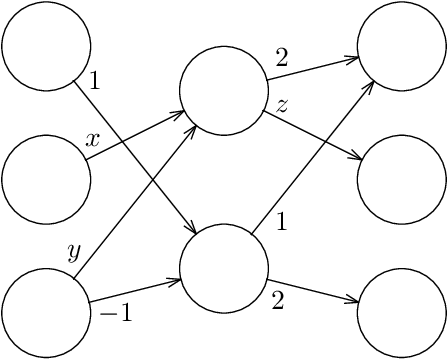
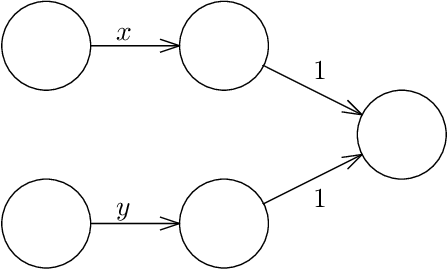
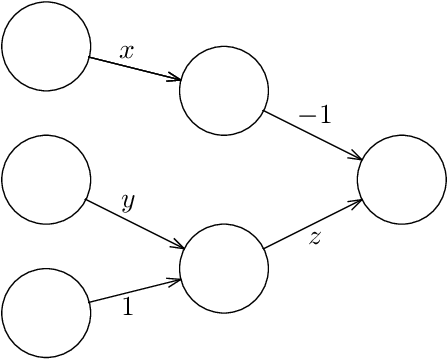
Given a neural network, training data, and a threshold, it was known that it is NP-hard to find weights for the neural network such that the total error is below the threshold. We determine the algorithmic complexity of this fundamental problem precisely, by showing that it is ER-complete. This means that the problem is equivalent, up to polynomial-time reductions, to deciding whether a system of polynomial equations and inequalities with integer coefficients and real unknowns has a solution. If, as widely expected, ER is strictly larger than NP, our work implies that the problem of training neural networks is not even in NP.
* 14 pages, 9 figures
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge