Michael Amir
When Is Diversity Rewarded in Cooperative Multi-Agent Learning?
Jun 11, 2025Abstract:The success of teams in robotics, nature, and society often depends on the division of labor among diverse specialists; however, a principled explanation for when such diversity surpasses a homogeneous team is still missing. Focusing on multi-agent task allocation problems, our goal is to study this question from the perspective of reward design: what kinds of objectives are best suited for heterogeneous teams? We first consider an instantaneous, non-spatial setting where the global reward is built by two generalized aggregation operators: an inner operator that maps the $N$ agents' effort allocations on individual tasks to a task score, and an outer operator that merges the $M$ task scores into the global team reward. We prove that the curvature of these operators determines whether heterogeneity can increase reward, and that for broad reward families this collapses to a simple convexity test. Next, we ask what incentivizes heterogeneity to emerge when embodied, time-extended agents must learn an effort allocation policy. To study heterogeneity in such settings, we use multi-agent reinforcement learning (MARL) as our computational paradigm, and introduce Heterogeneous Environment Design (HED), a gradient-based algorithm that optimizes the parameter space of underspecified MARL environments to find scenarios where heterogeneity is advantageous. Experiments in matrix games and an embodied Multi-Goal-Capture environment show that, despite the difference in settings, HED rediscovers the reward regimes predicted by our theory to maximize the advantage of heterogeneity, both validating HED and connecting our theoretical insights to reward design in MARL. Together, these results help us understand when behavioral diversity delivers a measurable benefit.
Time, Travel, and Energy in the Uniform Dispersion Problem
Apr 30, 2024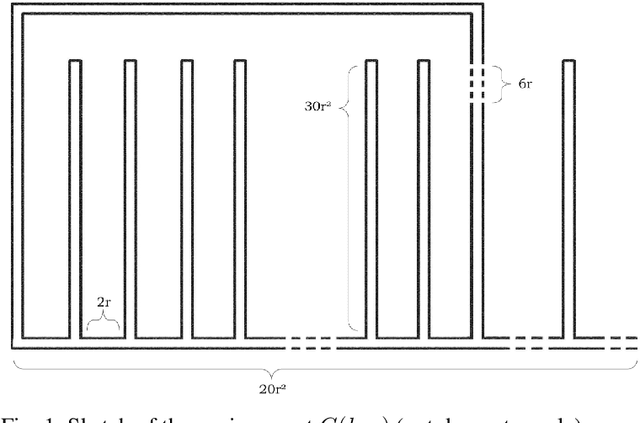

Abstract:We investigate the algorithmic problem of uniformly dispersing a swarm of robots in an unknown, gridlike environment. In this setting, our goal is to comprehensively study the relationships between performance metrics and robot capabilities. We introduce a formal model comparing dispersion algorithms based on makespan, traveled distance, energy consumption, sensing, communication, and memory. Using this framework, we classify several uniform dispersion algorithms according to their capability requirements and performance. We prove that while makespan and travel can be minimized in all environments, energy cannot, as long as the swarm's sensing range is bounded. In contrast, we show that energy can be minimized even by simple, ``ant-like" robots in synchronous settings and asymptotically minimized in asynchronous settings, provided the environment is topologically simply connected. Our findings offer insights into fundamental limitations that arise when designing swarm robotics systems for exploring unknown environments, highlighting the impact of environment's topology on the feasibility of energy-efficient dispersion.
Patrolling Grids with a Bit of Memory
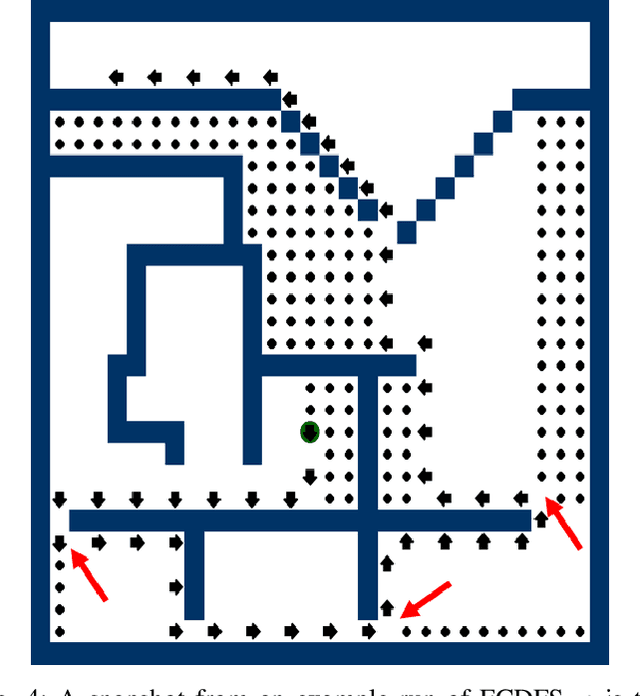
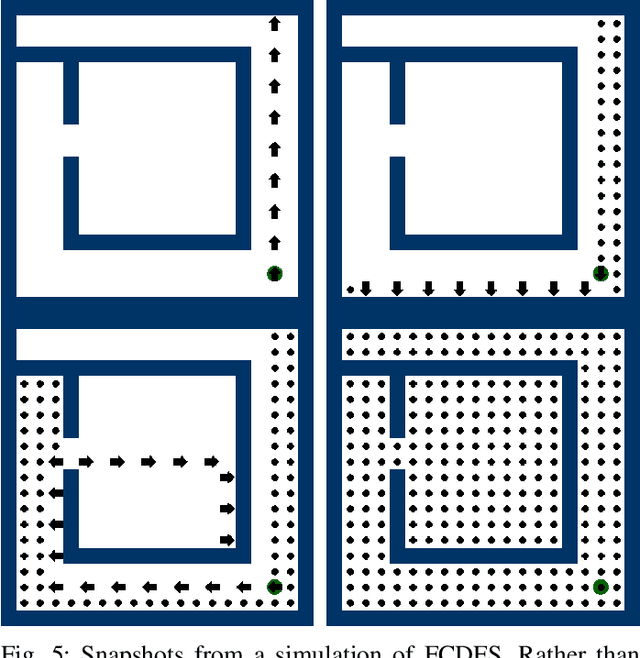
Jul 18, 2023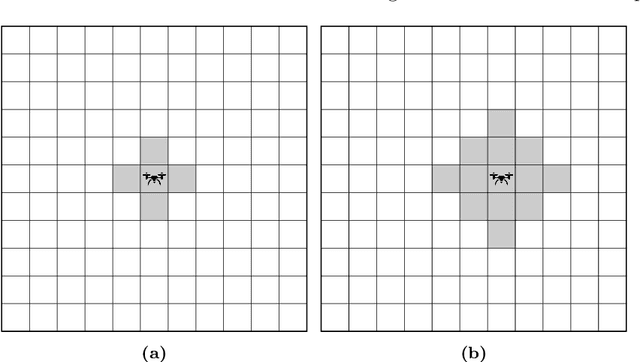
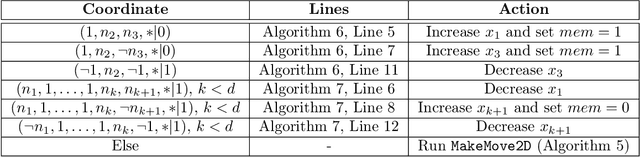
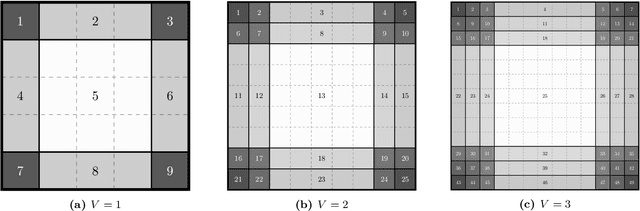
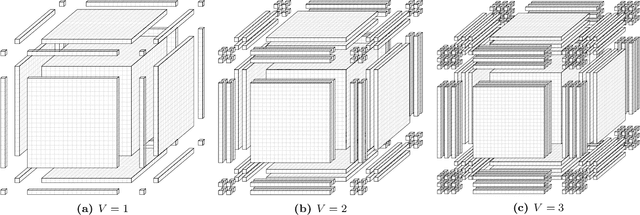
Abstract:We study the following problem in elementary robotics: can a mobile agent with $b$ bits of memory, which is able to sense only locations at Manhattan distance $V$ or less from itself, patrol a $d$-dimensional grid graph? We show that it is impossible to patrol some grid graphs with $0$ bits of memory, regardless of $V$, and give an exact characterization of those grid graphs that can be patrolled with $0$ bits of memory and visibility range $V$. On the other hand, we show that, surprisingly, an algorithm exists using $1$ bit of memory and $V=1$ that patrols any $d$-dimensional grid graph.
Probabilistic Pursuits on Graphs
Oct 29, 2017
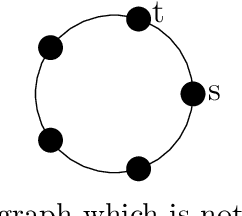


Abstract:We consider discrete dynamical systems of "ant-like" agents engaged in a sequence of pursuits on a graph environment. The agents emerge one by one at equal time intervals from a source vertex $s$ and pursue each other by greedily attempting to close the distance to their immediate predecessor, the agent that emerged just before them from $s$, until they arrive at the destination point $t$. Such pursuits have been investigated before in the continuous setting and in discrete time when the underlying environment is a regular grid. In both these settings the agents' walks provably converge to a shortest path from $s$ to $t$. Furthermore, assuming a certain natural probability distribution over the move choices of the agents on the grid (in case there are multiple shortest paths between an agent and its predecessor), the walks converge to the uniform distribution over all shortest paths from $s$ to $t$. We study the evolution of agent walks over a general finite graph environment $G$. Our model is a natural generalization of the pursuit rule proposed for the case of the grid. The main results are as follows. We show that "convergence" to the shortest paths in the sense of previous work extends to all pseudo-modular graphs (i.e. graphs in which every three pairwise intersecting disks have a nonempty intersection), and also to environments obtained by taking graph products, generalizing previous results in two different ways. We show that convergence to the shortest paths is also obtained by chordal graphs, and discuss some further positive and negative results for planar graphs. In the most general case, convergence to the shortest paths is not guaranteed, and the agents may get stuck on sets of recurrent, non-optimal walks from $s$ to $t$. However, we show that the limiting distributions of the agents' walks will always be uniform distributions over some set of walks of equal length.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge