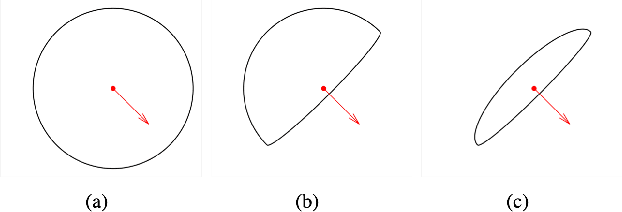
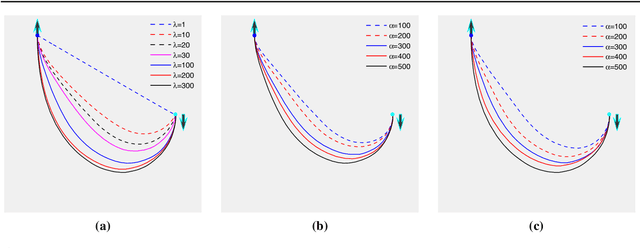
Geodesic Models with Convexity Shape Prior

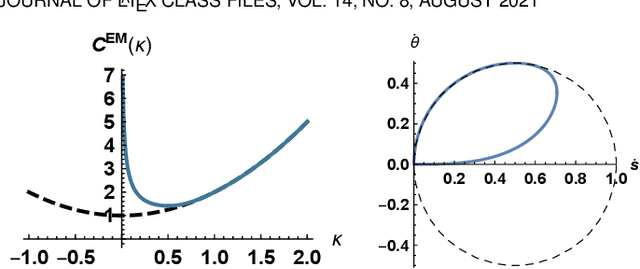
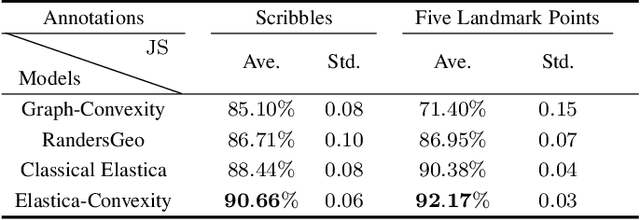
The minimal geodesic models based on the Eikonal equations are capable of finding suitable solutions in various image segmentation scenarios. Existing geodesic-based segmentation approaches usually exploit image features in conjunction with geometric regularization terms, such as Euclidean curve length or curvature-penalized length, for computing geodesic curves. In this paper, we take into account a more complicated problem: finding curvature-penalized geodesic paths with a convexity shape prior. We establish new geodesic models relying on the strategy of orientation-lifting, by which a planar curve can be mapped to an high-dimensional orientation-dependent space. The convexity shape prior serves as a constraint for the construction of local geodesic metrics encoding a particular curvature constraint. Then the geodesic distances and the corresponding closed geodesic paths in the orientation-lifted space can be efficiently computed through state-of-the-art Hamiltonian fast marching method. In addition, we apply the proposed geodesic models to the active contours, leading to efficient interactive image segmentation algorithms that preserve the advantages of convexity shape prior and curvature penalization.

A Generalized Asymmetric Dual-front Model for Active Contours and Image Segmentation

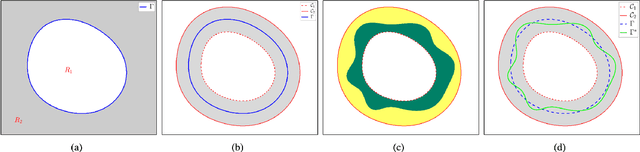
The geodesic distance-based dual-front curve evolution model is a powerful and efficient solution to the active contours and image segmentation issues. In its basic formulation, the dual-front model regards the meeting interfaces of two adjacent Voronoi regions as the evolving curves in the course of curve evolution. One of the most crucial ingredients for the construction of Voronoi regions or Voronoi diagram is the geodesic metrics and the corresponding geodesic distance. In this paper, we introduce a new type of geodesic metrics that encodes the edge-based anisotropy features, the region-based homogeneity penalization and asymmetric enhancement. In contrast to the original isotropic dual-front model, the use of the asymmetric enhancement can reduce the risk of shortcuts or leakage problems especially when the initial curves are far away from the target boundaries. Moreover, the proposed dual-front model can be applied for image segmentation in conjunction with various region-based homogeneity terms, whereas the original model only makes use of the piecewise constant case. The numerical experiments on both synthetic and real images show that the proposed model indeed achieves encouraging results.

Eikonal Region-based Active Contours for Image Segmentation

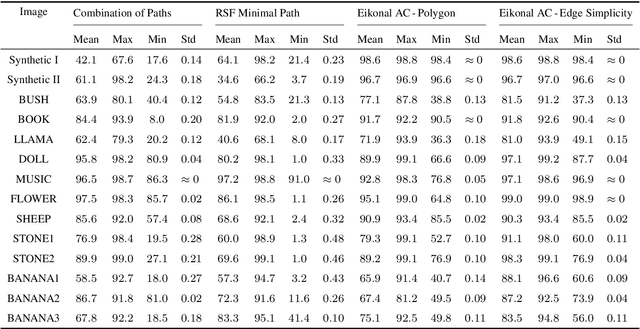
The minimal path model based on the Eikonal partial differential equation (PDE) has served as a fundamental tool for the applications of image segmentation and boundary detection in the passed three decades. However, the existing minimal paths-based image segmentation approaches commonly rely on the image boundary features, potentially limiting their performance in some situations. In this paper, we introduce a new variational image segmentation model based on the minimal path framework and the Eikonal PDE, where the region-based functional that defines the homogeneity criteria can be taken into account for estimating the associated geodesic paths. This is done by establishing a geodesic curve interpretation to the region-based active contour evolution problem. The image segmentation processing is carried out in an iterative manner in our approach. A crucial ingredient in each iteration is to construct an asymmetric Randers geodesic metric using a sufficiently small vector field, such that a set of geodesic paths can be tracked from the geodesic distance map which is the solution to an Eikonal PDE. The object boundary can be delineated by the concatenation of the final geodesic paths. We invoke the Finsler variant of the fast marching method to estimate the geodesic distance map, yielding an efficient implementation of the proposed Eikonal region-based active contour model. Experimental results on both of the synthetic and real images exhibit that our model indeed achieves encouraging segmentation performance.

Global Minimum for a Finsler Elastica Minimal Path Approach

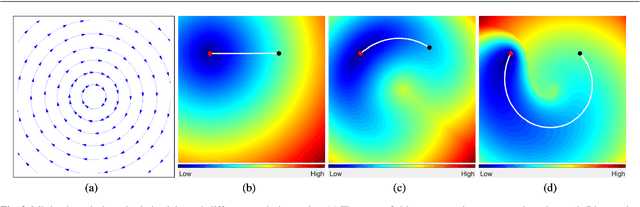
In this paper, we propose a novel curvature-penalized minimal path model via an orientation-lifted Finsler metric and the Euler elastica curve. The original minimal path model computes the globally minimal geodesic by solving an Eikonal partial differential equation (PDE). Essentially, this first-order model is unable to penalize curvature which is related to the path rigidity property in the classical active contour models. To solve this problem, we present an Eikonal PDE-based Finsler elastica minimal path approach to address the curvature-penalized geodesic energy minimization problem. We were successful at adding the curvature penalization to the classical geodesic energy. The basic idea of this work is to interpret the Euler elastica bending energy via a novel Finsler elastica metric that embeds a curvature penalty. This metric is non-Riemannian, anisotropic and asymmetric, and is defined over an orientation-lifted space by adding to the image domain the orientation as an extra space dimension. Based on this orientation lifting, the proposed minimal path model can benefit from both the curvature and orientation of the paths. Thanks to the fast marching method, the global minimum of the curvature-penalized geodesic energy can be computed efficiently. We introduce two anisotropic image data-driven speed functions that are computed by steerable filters. Based on these orientation-dependent speed functions, we can apply the proposed Finsler elastica minimal path model to the applications of closed contour detection, perceptual grouping and tubular structure extraction. Numerical experiments on both synthetic and real images show that these applications of the proposed model indeed obtain promising results.

Anisotropic Diffusion in ITK

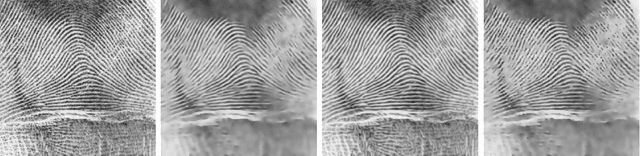
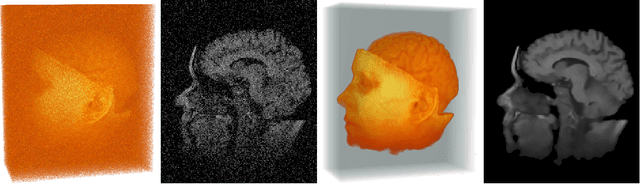
Anisotropic Non-Linear Diffusion is a powerful image processing technique, which allows to simultaneously remove the noise and enhance sharp features in two or three dimensional images. Anisotropic Diffusion is understood here in the sense of Weickert, meaning that diffusion tensors are anisotropic and reflect the local orientation of image features. This is in contrast with the non-linear diffusion filter of Perona and Malik, which only involves scalar diffusion coefficients, in other words isotropic diffusion tensors. In this paper, we present an anisotropic non-linear diffusion technique we implemented in ITK. This technique is based on a recent adaptive scheme making the diffusion stable and requiring limited numerical resources. (See supplementary data.)