A Generalized Asymmetric Dual-front Model for Active Contours and Image Segmentation

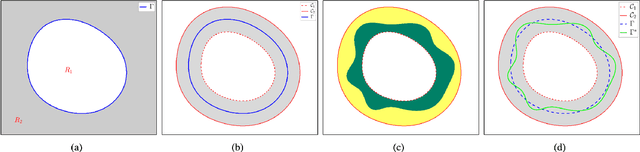
The geodesic distance-based dual-front curve evolution model is a powerful and efficient solution to the active contours and image segmentation issues. In its basic formulation, the dual-front model regards the meeting interfaces of two adjacent Voronoi regions as the evolving curves in the course of curve evolution. One of the most crucial ingredients for the construction of Voronoi regions or Voronoi diagram is the geodesic metrics and the corresponding geodesic distance. In this paper, we introduce a new type of geodesic metrics that encodes the edge-based anisotropy features, the region-based homogeneity penalization and asymmetric enhancement. In contrast to the original isotropic dual-front model, the use of the asymmetric enhancement can reduce the risk of shortcuts or leakage problems especially when the initial curves are far away from the target boundaries. Moreover, the proposed dual-front model can be applied for image segmentation in conjunction with various region-based homogeneity terms, whereas the original model only makes use of the piecewise constant case. The numerical experiments on both synthetic and real images show that the proposed model indeed achieves encouraging results.

Chan-Vese Reformulation for Selective Image Segmentation

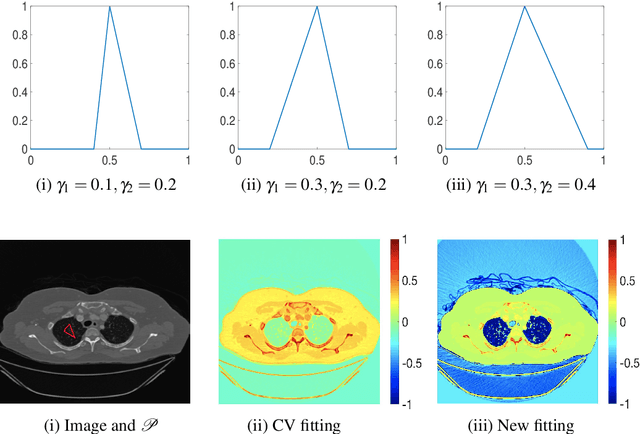
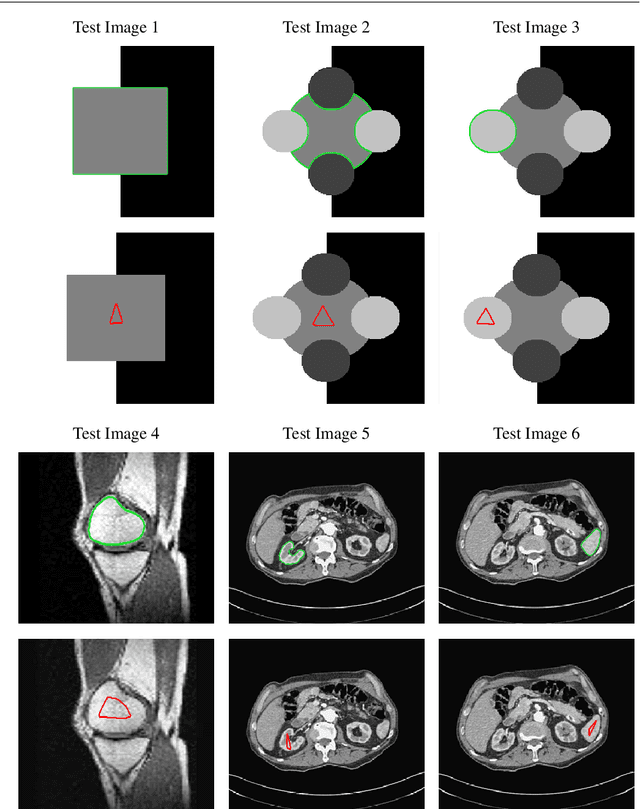
Selective segmentation involves incorporating user input to partition an image into foreground and background, by discriminating between objects of a similar type. Typically, such methods involve introducing additional constraints to generic segmentation approaches. However, we show that this is often inconsistent with respect to common assumptions about the image. The proposed method introduces a new fitting term that is more useful in practice than the Chan-Vese framework. In particular, the idea is to define a term that allows for the background to consist of multiple regions of inhomogeneity. We provide comparitive experimental results to alternative approaches to demonstrate the advantages of the proposed method, broadening the possible application of these methods.

A Restricted-Domain Dual Formulation for Two-Phase Image Segmentation

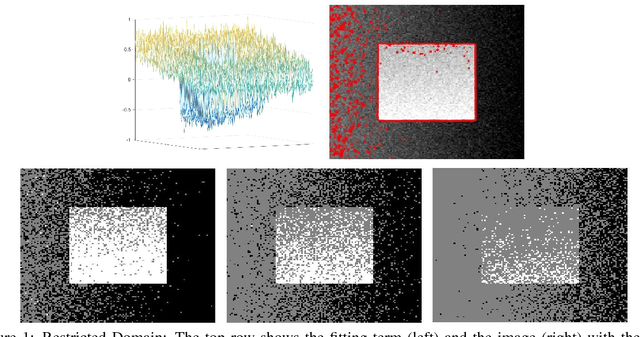
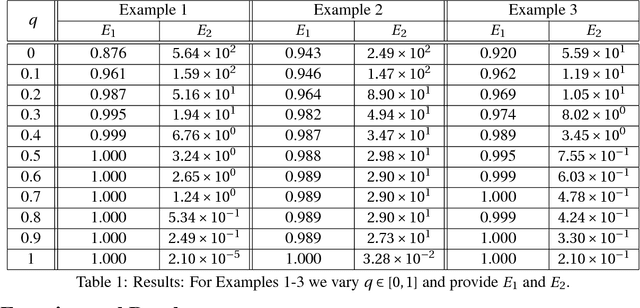
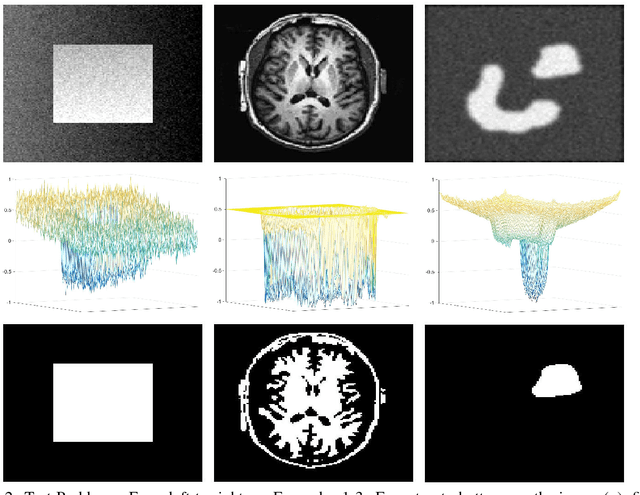
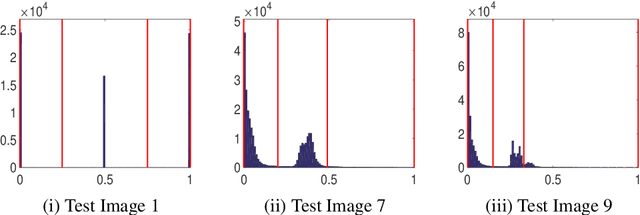
In two-phase image segmentation, convex relaxation has allowed global minimisers to be computed for a variety of data fitting terms. Many efficient approaches exist to compute a solution quickly. However, we consider whether the nature of the data fitting in this formulation allows for reasonable assumptions to be made about the solution that can improve the computational performance further. In particular, we employ a well known dual formulation of this problem and solve the corresponding equations in a restricted domain. We present experimental results that explore the dependence of the solution on this restriction and quantify imrovements in the computational performance. This approach can be extended to analogous methods simply and could provide an efficient alternative for problems of this type.