Eikonal Region-based Active Contours for Image Segmentation

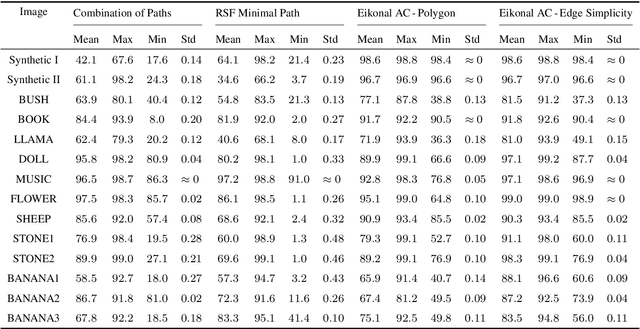
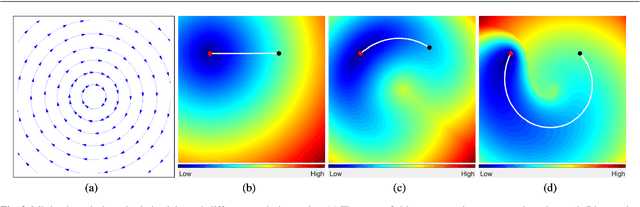
The minimal path model based on the Eikonal partial differential equation (PDE) has served as a fundamental tool for the applications of image segmentation and boundary detection in the passed three decades. However, the existing minimal paths-based image segmentation approaches commonly rely on the image boundary features, potentially limiting their performance in some situations. In this paper, we introduce a new variational image segmentation model based on the minimal path framework and the Eikonal PDE, where the region-based functional that defines the homogeneity criteria can be taken into account for estimating the associated geodesic paths. This is done by establishing a geodesic curve interpretation to the region-based active contour evolution problem. The image segmentation processing is carried out in an iterative manner in our approach. A crucial ingredient in each iteration is to construct an asymmetric Randers geodesic metric using a sufficiently small vector field, such that a set of geodesic paths can be tracked from the geodesic distance map which is the solution to an Eikonal PDE. The object boundary can be delineated by the concatenation of the final geodesic paths. We invoke the Finsler variant of the fast marching method to estimate the geodesic distance map, yielding an efficient implementation of the proposed Eikonal region-based active contour model. Experimental results on both of the synthetic and real images exhibit that our model indeed achieves encouraging segmentation performance.