Chan-Vese Attention U-Net: An attention mechanism for robust segmentation

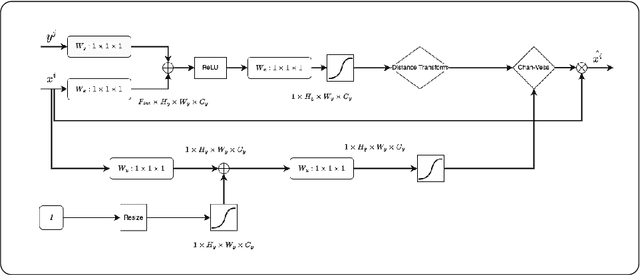
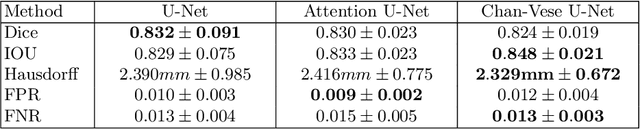
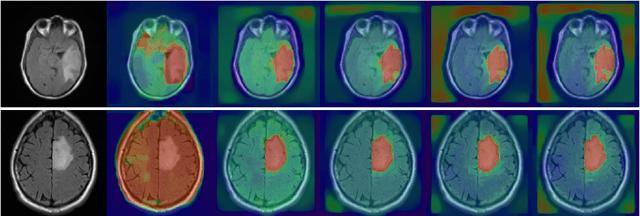
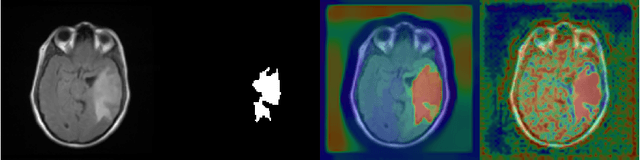
When studying the results of a segmentation algorithm using convolutional neural networks, one wonders about the reliability and consistency of the results. This leads to questioning the possibility of using such an algorithm in applications where there is little room for doubt. We propose in this paper a new attention gate based on the use of Chan-Vese energy minimization to control more precisely the segmentation masks given by a standard CNN architecture such as the U-Net model. This mechanism allows to obtain a constraint on the segmentation based on the resolution of a PDE. The study of the results allows us to observe the spatial information retained by the neural network on the region of interest and obtains competitive results on the binary segmentation. We illustrate the efficiency of this approach for medical image segmentation on a database of MRI brain images.

Fast Marching Energy CNN

Leveraging geodesic distances and the geometrical information they convey is key for many data-oriented applications in imaging. Geodesic distance computation has been used for long for image segmentation using Image based metrics. We introduce a new method by generating isotropic Riemannian metrics adapted to a problem using CNN and give as illustrations an example of application. We then apply this idea to the segmentation of brain tumours as unit balls for the geodesic distance computed with the metric potential output by a CNN, thus imposing geometrical and topological constraints on the output mask. We show that geodesic distance modules work well in machine learning frameworks and can be used to achieve state-of-the-art performances while ensuring geometrical and/or topological properties.