Hierarchical Conditional Multi-Task Learning for Streamflow Modeling

Streamflow, vital for water resource management, is governed by complex hydrological systems involving intermediate processes driven by meteorological forces. While deep learning models have achieved state-of-the-art results of streamflow prediction, their end-to-end single-task learning approach often fails to capture the causal relationships within these systems. To address this, we propose Hierarchical Conditional Multi-Task Learning (HCMTL), a hierarchical approach that jointly models soil water and snowpack processes based on their causal connections to streamflow. HCMTL utilizes task embeddings to connect network modules, enhancing flexibility and expressiveness while capturing unobserved processes beyond soil water and snowpack. It also incorporates the Conditional Mini-Batch strategy to improve long time series modeling. We compare HCMTL with five baselines on a global dataset. HCMTL's superior performance across hundreds of drainage basins over extended periods shows that integrating domain-specific causal knowledge into deep learning enhances both prediction accuracy and interpretability. This is essential for advancing our understanding of complex hydrological systems and supporting efficient water resource management to mitigate natural disasters like droughts and floods.

ExoTST: Exogenous-Aware Temporal Sequence Transformer for Time Series Prediction

Accurate long-term predictions are the foundations for many machine learning applications and decision-making processes. Traditional time series approaches for prediction often focus on either autoregressive modeling, which relies solely on past observations of the target ``endogenous variables'', or forward modeling, which considers only current covariate drivers ``exogenous variables''. However, effectively integrating past endogenous and past exogenous with current exogenous variables remains a significant challenge. In this paper, we propose ExoTST, a novel transformer-based framework that effectively incorporates current exogenous variables alongside past context for improved time series prediction. To integrate exogenous information efficiently, ExoTST leverages the strengths of attention mechanisms and introduces a novel cross-temporal modality fusion module. This module enables the model to jointly learn from both past and current exogenous series, treating them as distinct modalities. By considering these series separately, ExoTST provides robustness and flexibility in handling data uncertainties that arise from the inherent distribution shift between historical and current exogenous variables. Extensive experiments on real-world carbon flux datasets and time series benchmarks demonstrate ExoTST's superior performance compared to state-of-the-art baselines, with improvements of up to 10\% in prediction accuracy. Moreover, ExoTST exhibits strong robustness against missing values and noise in exogenous drivers, maintaining consistent performance in real-world situations where these imperfections are common.

Koopman Invertible Autoencoder: Leveraging Forward and Backward Dynamics for Temporal Modeling

Accurate long-term predictions are the foundations for many machine learning applications and decision-making processes. However, building accurate long-term prediction models remains challenging due to the limitations of existing temporal models like recurrent neural networks (RNNs), as they capture only the statistical connections in the training data and may fail to learn the underlying dynamics of the target system. To tackle this challenge, we propose a novel machine learning model based on Koopman operator theory, which we call Koopman Invertible Autoencoders (KIA), that captures the inherent characteristic of the system by modeling both forward and backward dynamics in the infinite-dimensional Hilbert space. This enables us to efficiently learn low-dimensional representations, resulting in more accurate predictions of long-term system behavior. Moreover, our method's invertibility design guarantees reversibility and consistency in both forward and inverse operations. We illustrate the utility of KIA on pendulum and climate datasets, demonstrating 300% improvements in long-term prediction capability for pendulum while maintaining robustness against noise. Additionally, our method excels in long-term climate prediction, further validating our method's effectiveness.

Phase Retrieval using Single-Instance Deep Generative Prior

Several deep learning methods for phase retrieval exist, but most of them fail on realistic data without precise support information. We propose a novel method based on single-instance deep generative prior that works well on complex-valued crystal data.

Inverse Problems, Deep Learning, and Symmetry Breaking

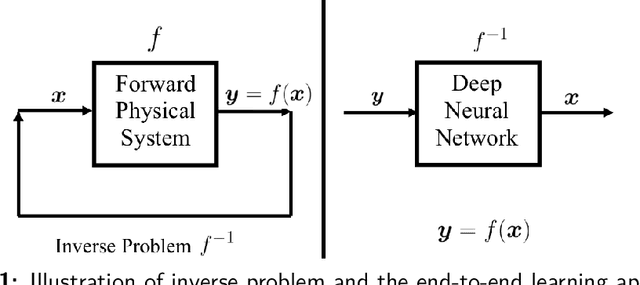
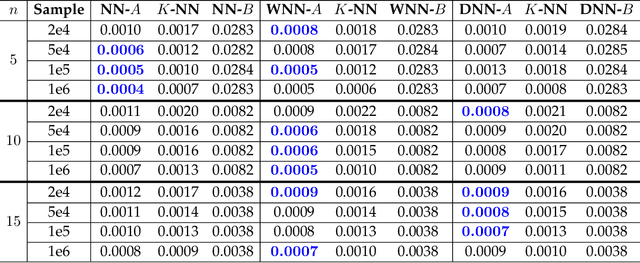
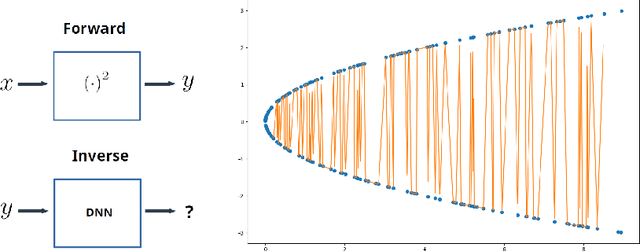
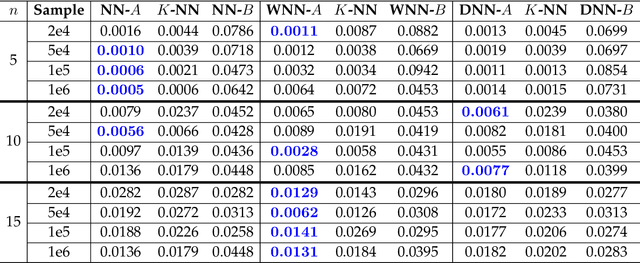
In many physical systems, inputs related by intrinsic system symmetries are mapped to the same output. When inverting such systems, i.e., solving the associated inverse problems, there is no unique solution. This causes fundamental difficulties for deploying the emerging end-to-end deep learning approach. Using the generalized phase retrieval problem as an illustrative example, we show that careful symmetry breaking on the training data can help get rid of the difficulties and significantly improve the learning performance. We also extract and highlight the underlying mathematical principle of the proposed solution, which is directly applicable to other inverse problems.