Inverse Problems, Deep Learning, and Symmetry Breaking
Paper and Code
Mar 20, 2020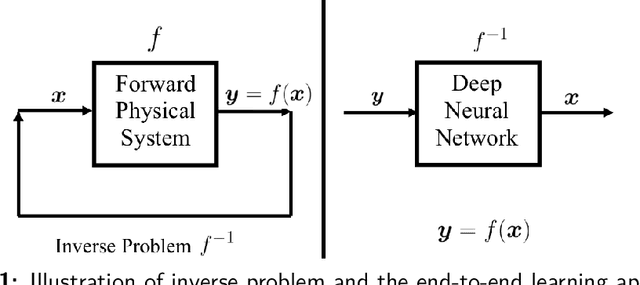
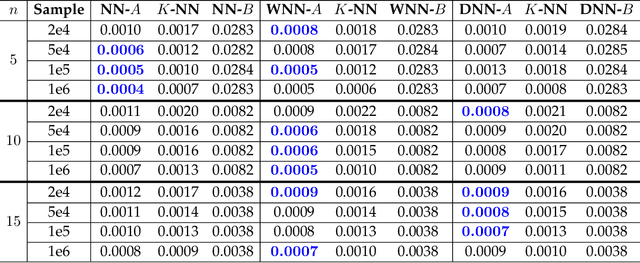
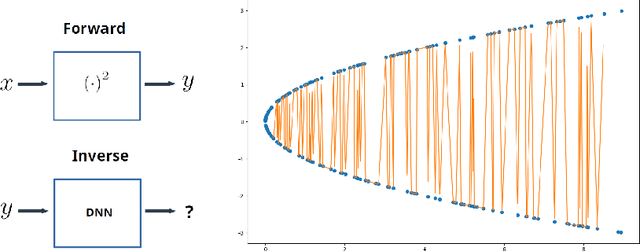
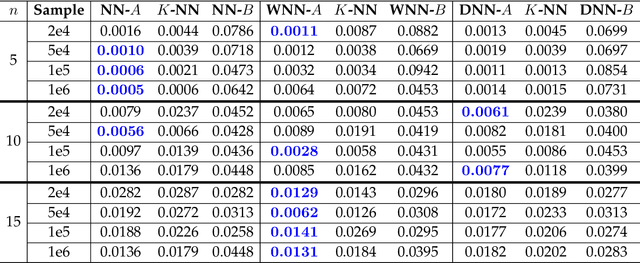
In many physical systems, inputs related by intrinsic system symmetries are mapped to the same output. When inverting such systems, i.e., solving the associated inverse problems, there is no unique solution. This causes fundamental difficulties for deploying the emerging end-to-end deep learning approach. Using the generalized phase retrieval problem as an illustrative example, we show that careful symmetry breaking on the training data can help get rid of the difficulties and significantly improve the learning performance. We also extract and highlight the underlying mathematical principle of the proposed solution, which is directly applicable to other inverse problems.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge