Statistical modelling and Bayesian inversion for a Compton imaging system: application to radioactive source localisation

This paper presents a statistical forward model for a Compton imaging system, called Compton imager. This system, under development at the University of Illinois Urbana Champaign, is a variant of Compton cameras with a single type of sensors which can simultaneously act as scatterers and absorbers. This imager is convenient for imaging situations requiring a wide field of view. The proposed statistical forward model is then used to solve the inverse problem of estimating the location and energy of point-like sources from observed data. This inverse problem is formulated and solved in a Bayesian framework by using a Metropolis within Gibbs algorithm for the estimation of the location, and an expectation-maximization algorithm for the estimation of the energy. This approach leads to more accurate estimation when compared with the deterministic standard back-projection approach, with the additional benefit of uncertainty quantification in the low photon imaging setting.

A Variational Perspective on High-Resolution ODEs

We consider unconstrained minimization of smooth convex functions. We propose a novel variational perspective using forced Euler-Lagrange equation that allows for studying high-resolution ODEs. Through this, we obtain a faster convergence rate for gradient norm minimization using Nesterov's accelerated gradient method. Additionally, we show that Nesterov's method can be interpreted as a rate-matching discretization of an appropriately chosen high-resolution ODE. Finally, using the results from the new variational perspective, we propose a stochastic method for noisy gradients. Several numerical experiments compare and illustrate our stochastic algorithm with state of the art methods.

Accelerated Bayesian imaging by relaxed proximal-point Langevin sampling

This paper presents a new accelerated proximal Markov chain Monte Carlo methodology to perform Bayesian inference in imaging inverse problems with an underlying convex geometry. The proposed strategy takes the form of a stochastic relaxed proximal-point iteration that admits two complementary interpretations. For models that are smooth or regularised by Moreau-Yosida smoothing, the algorithm is equivalent to an implicit midpoint discretisation of an overdamped Langevin diffusion targeting the posterior distribution of interest. This discretisation is asymptotically unbiased for Gaussian targets and shown to converge in an accelerated manner for any target that is $\kappa$-strongly log-concave (i.e., requiring in the order of $\sqrt{\kappa}$ iterations to converge, similarly to accelerated optimisation schemes), comparing favorably to [M. Pereyra, L. Vargas Mieles, K.C. Zygalakis, SIAM J. Imaging Sciences, 13, 2 (2020), pp. 905-935] which is only provably accelerated for Gaussian targets and has bias. For models that are not smooth, the algorithm is equivalent to a Leimkuhler-Matthews discretisation of a Langevin diffusion targeting a Moreau-Yosida approximation of the posterior distribution of interest, and hence achieves a significantly lower bias than conventional unadjusted Langevin strategies based on the Euler-Maruyama discretisation. For targets that are $\kappa$-strongly log-concave, the provided non-asymptotic convergence analysis also identifies the optimal time step which maximizes the convergence speed. The proposed methodology is demonstrated through a range of experiments related to image deconvolution with Gaussian and Poisson noise, with assumption-driven and data-driven convex priors.

Gaussian processes for Bayesian inverse problems associated with linear partial differential equations

This work is concerned with the use of Gaussian surrogate models for Bayesian inverse problems associated with linear partial differential equations. A particular focus is on the regime where only a small amount of training data is available. In this regime the type of Gaussian prior used is of critical importance with respect to how well the surrogate model will perform in terms of Bayesian inversion. We extend the framework of Raissi et. al. (2017) to construct PDE-informed Gaussian priors that we then use to construct different approximate posteriors. A number of different numerical experiments illustrate the superiority of the PDE-informed Gaussian priors over more traditional priors.

The split Gibbs sampler revisited: improvements to its algorithmic structure and augmented target distribution

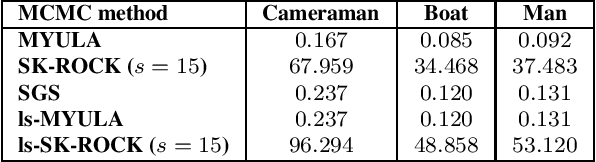
This paper proposes a new accelerated proximal Markov chain Monte Carlo (MCMC) methodology to perform Bayesian computation efficiently in imaging inverse problems. The proposed methodology is derived from the Langevin diffusion process and stems from tightly integrating two state-of-the-art proximal Langevin MCMC samplers, SK-ROCK and split Gibbs sampling (SGS), which employ distinctively different strategies to improve convergence speed. More precisely, we show how to integrate, at the level of the Langevin diffusion process, the proximal SK-ROCK sampler which is based on a stochastic Runge-Kutta-Chebyshev approximation of the diffusion, with the model augmentation and relaxation strategy that SGS exploits to speed up Bayesian computation at the expense of asymptotic bias. This leads to a new and faster proximal SK-ROCK sampler that combines the accelerated quality of the original SK-ROCK sampler with the computational benefits of augmentation and relaxation. Moreover, rather than viewing the augmented and relaxed model as an approximation of the target model, positioning relaxation in a bias-variance trade-off, we propose to regard the augmented and relaxed model as a generalisation of the target model. This then allows us to carefully calibrate the amount of relaxation in order to simultaneously improve the accuracy of the model (as measured by the model evidence) and the sampler's convergence speed. To achieve this, we derive an empirical Bayesian method to automatically estimate the optimal amount of relaxation by maximum marginal likelihood estimation. The proposed methodology is demonstrated with a range of numerical experiments related to image deblurring and inpainting, as well as with comparisons with alternative approaches from the state of the art.

Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations

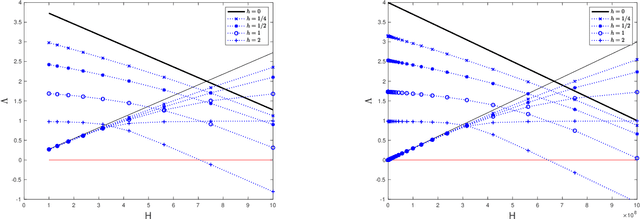
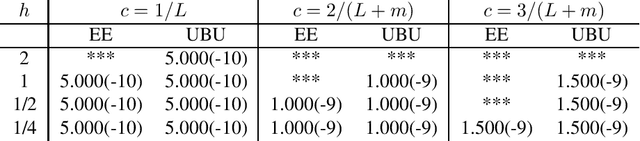
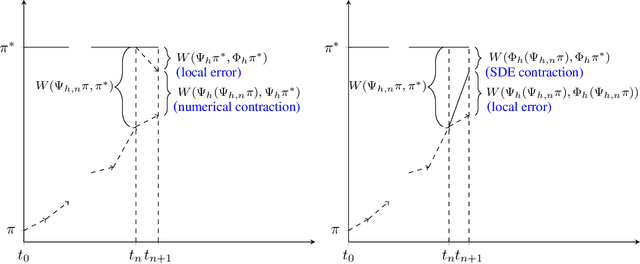
We present a framework that allows for the non-asymptotic study of the $2$-Wasserstein distance between the invariant distribution of an ergodic stochastic differential equation and the distribution of its numerical approximation in the strongly log-concave case. This allows us to study in a unified way a number of different integrators proposed in the literature for the overdamped and underdamped Langevin dynamics. In addition, we analyse a novel splitting method for the underdamped Langevin dynamics which only requires one gradient evaluation per time step. Under an additional smoothness assumption on a $d$--dimensional strongly log-concave distribution with condition number $\kappa$, the algorithm is shown to produce with an $\mathcal{O}\big(\kappa^{5/4} d^{1/4}\epsilon^{-1/2} \big)$ complexity samples from a distribution that, in Wasserstein distance, is at most $\epsilon>0$ away from the target distribution.

Bayesian Imaging With Data-Driven Priors Encoded by Neural Networks: Theory, Methods, and Algorithms

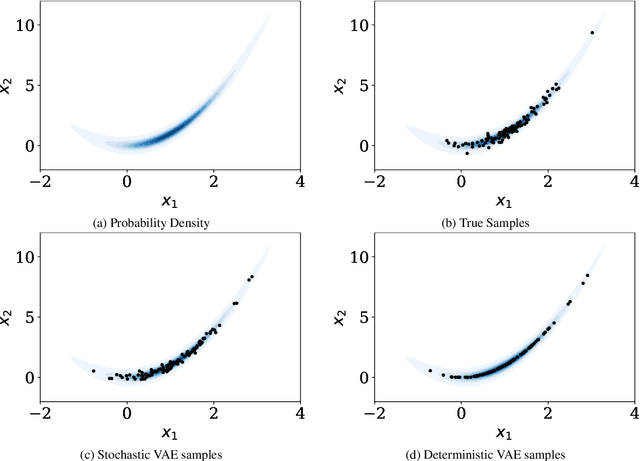
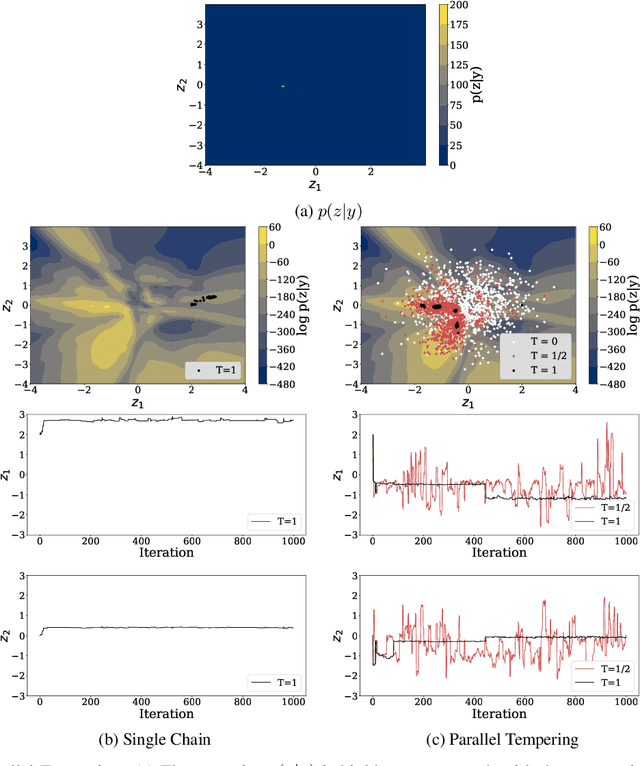
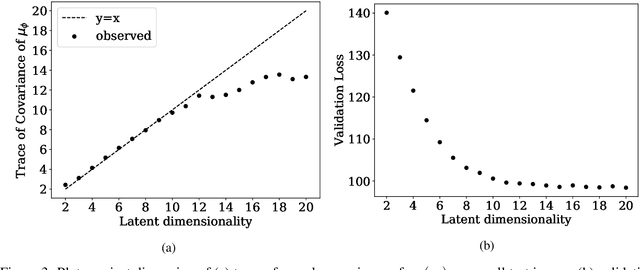
This paper proposes a new methodology for performing Bayesian inference in imaging inverse problems where the prior knowledge is available in the form of training data. Following the manifold hypothesis and adopting a generative modelling approach, we construct a data-driven prior that is supported on a sub-manifold of the ambient space, which we can learn from the training data by using a variational autoencoder or a generative adversarial network. We establish the existence and well-posedness of the associated posterior distribution and posterior moments under easily verifiable conditions, providing a rigorous underpinning for Bayesian estimators and uncertainty quantification analyses. Bayesian computation is performed by using a parallel tempered version of the preconditioned Crank-Nicolson algorithm on the manifold, which is shown to be ergodic and robust to the non-convex nature of these data-driven models. In addition to point estimators and uncertainty quantification analyses, we derive a model misspecification test to automatically detect situations where the data-driven prior is unreliable, and explain how to identify the dimension of the latent space directly from the training data. The proposed approach is illustrated with a range of experiments with the MNIST dataset, where it outperforms alternative image reconstruction approaches from the state of the art. A model accuracy analysis suggests that the Bayesian probabilities reported by the data-driven models are also remarkably accurate under a frequentist definition of probability.

A Linear Transportation $\mathrm{L}^p$ Distance for Pattern Recognition

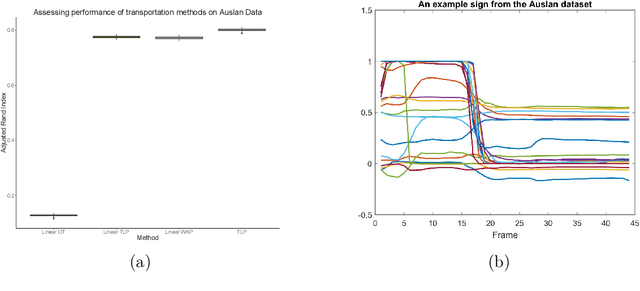
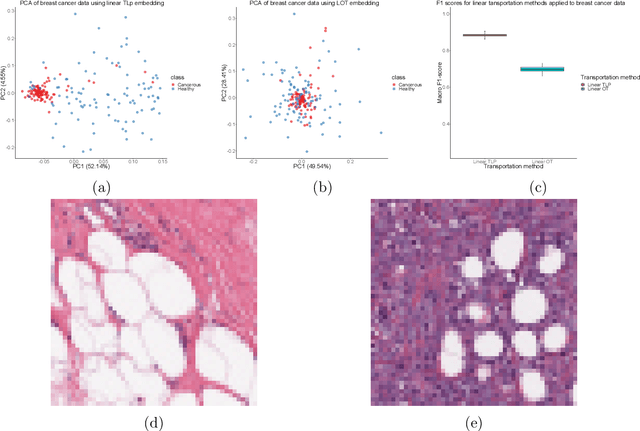
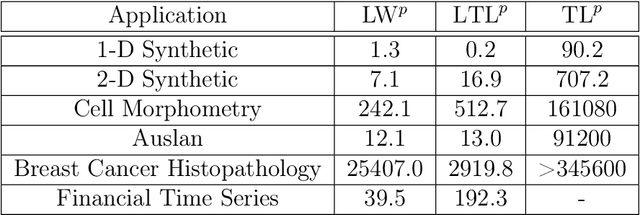
The transportation $\mathrm{L}^p$ distance, denoted $\mathrm{TL}^p$, has been proposed as a generalisation of Wasserstein $\mathrm{W}^p$ distances motivated by the property that it can be applied directly to colour or multi-channelled images, as well as multivariate time-series without normalisation or mass constraints. These distances, as with $\mathrm{W}^p$, are powerful tools in modelling data with spatial or temporal perturbations. However, their computational cost can make them infeasible to apply to even moderate pattern recognition tasks. We propose linear versions of these distances and show that the linear $\mathrm{TL}^p$ distance significantly improves over the linear $\mathrm{W}^p$ distance on signal processing tasks, whilst being several orders of magnitude faster to compute than the $\mathrm{TL}^p$ distance.

The connections between Lyapunov functions for some optimization algorithms and differential equations

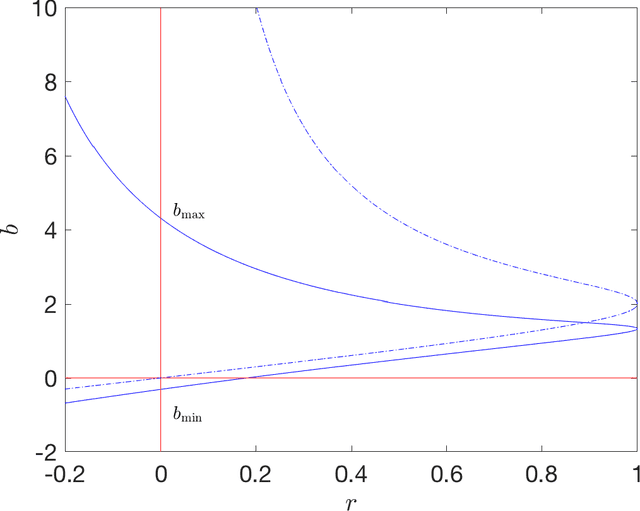
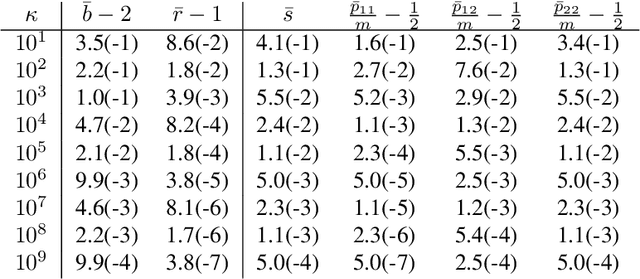
In this manuscript we study the properties of a family of a second order differential equations with damping, its discretizations and their connections with accelerated optimization algorithms for $m$-strongly convex and $L$-smooth functions. In particular, using the Linear Matrix Inequality framework developed in \emph{Fazlyab et. al. $(2018)$}, we derive analytically a (discrete) Lyapunov function for a two-parameter family of Nesterov optimization methods, which allows for a complete characterization of their convergence rate. We then show that in the appropriate limit this family of methods may be seen as a discretization of a family of second order ordinary differential equations, which properties can be also understood by a (continuous) Lyapunov function, which can also be obtained by studying the limiting behaviour of the discrete Lyapunov function. Finally, we show that the majority of typical discretizations of this ODE, such as the Heavy ball method, do not possess suitable discrete Lyapunov functions, and hence fail to reproduce the desired limiting behaviour of this ODE, which in turn implies that their converge rates when seen as optimization methods cannot behave in an "accerelated" manner .