Deep metric learning improves lab of origin prediction of genetically engineered plasmids

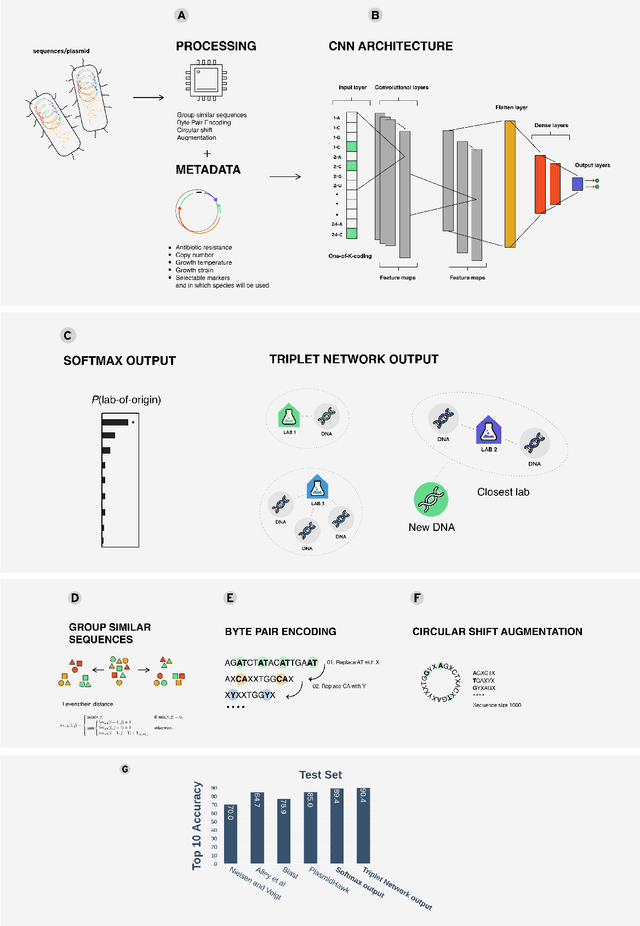
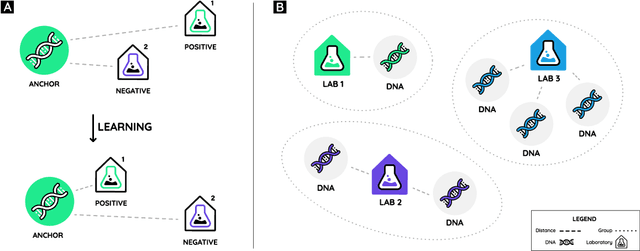
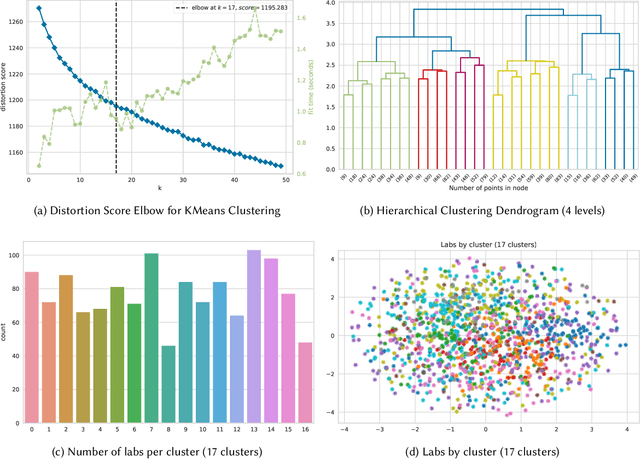
Genome engineering is undergoing unprecedented development and is now becoming widely available. To ensure responsible biotechnology innovation and to reduce misuse of engineered DNA sequences, it is vital to develop tools to identify the lab-of-origin of engineered plasmids. Genetic engineering attribution (GEA), the ability to make sequence-lab associations, would support forensic experts in this process. Here, we propose a method, based on metric learning, that ranks the most likely labs-of-origin whilst simultaneously generating embeddings for plasmid sequences and labs. These embeddings can be used to perform various downstream tasks, such as clustering DNA sequences and labs, as well as using them as features in machine learning models. Our approach employs a circular shift augmentation approach and is able to correctly rank the lab-of-origin $90\%$ of the time within its top 10 predictions - outperforming all current state-of-the-art approaches. We also demonstrate that we can perform few-shot-learning and obtain $76\%$ top-10 accuracy using only $10\%$ of the sequences. This means, we outperform the previous CNN approach using only one-tenth of the data. We also demonstrate that we are able to extract key signatures in plasmid sequences for particular labs, allowing for an interpretable examination of the model's outputs.

Analysis of the first Genetic Engineering Attribution Challenge

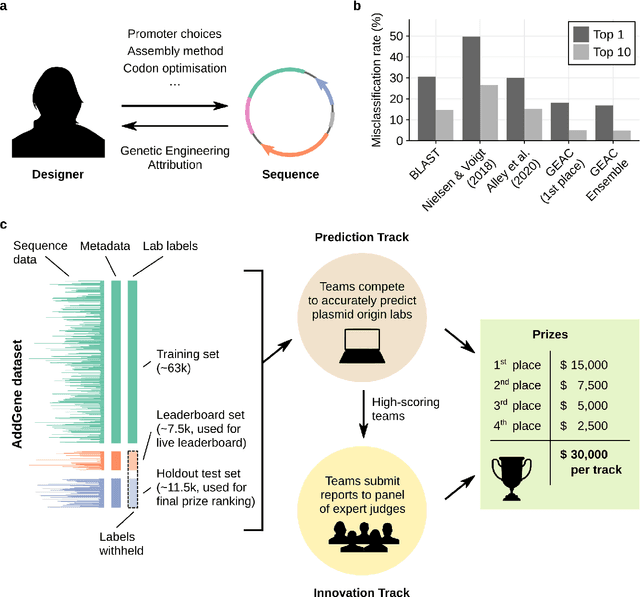
The ability to identify the designer of engineered biological sequences -- termed genetic engineering attribution (GEA) -- would help ensure due credit for biotechnological innovation, while holding designers accountable to the communities they affect. Here, we present the results of the first Genetic Engineering Attribution Challenge, a public data-science competition to advance GEA. Top-scoring teams dramatically outperformed previous models at identifying the true lab-of-origin of engineered sequences, including an increase in top-1 and top-10 accuracy of 10 percentage points. A simple ensemble of prizewinning models further increased performance. New metrics, designed to assess a model's ability to confidently exclude candidate labs, also showed major improvements, especially for the ensemble. Most winning teams adopted CNN-based machine-learning approaches; however, one team achieved very high accuracy with an extremely fast neural-network-free approach. Future work, including future competitions, should further explore a wide diversity of approaches for bringing GEA technology into practical use.

A Linear Transportation $\mathrm{L}^p$ Distance for Pattern Recognition

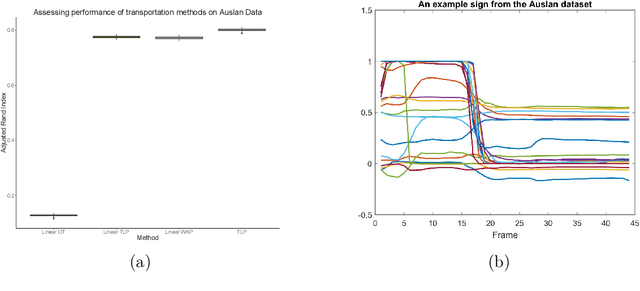
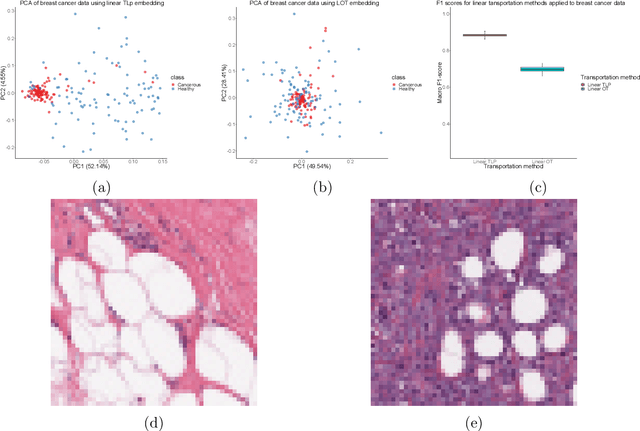
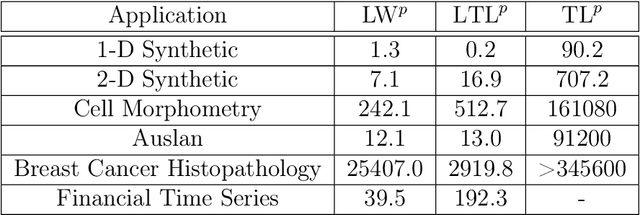
The transportation $\mathrm{L}^p$ distance, denoted $\mathrm{TL}^p$, has been proposed as a generalisation of Wasserstein $\mathrm{W}^p$ distances motivated by the property that it can be applied directly to colour or multi-channelled images, as well as multivariate time-series without normalisation or mass constraints. These distances, as with $\mathrm{W}^p$, are powerful tools in modelling data with spatial or temporal perturbations. However, their computational cost can make them infeasible to apply to even moderate pattern recognition tasks. We propose linear versions of these distances and show that the linear $\mathrm{TL}^p$ distance significantly improves over the linear $\mathrm{W}^p$ distance on signal processing tasks, whilst being several orders of magnitude faster to compute than the $\mathrm{TL}^p$ distance.

PDE-Inspired Algorithms for Semi-Supervised Learning on Point Clouds

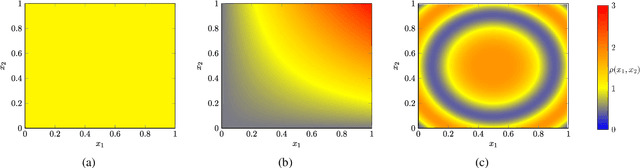
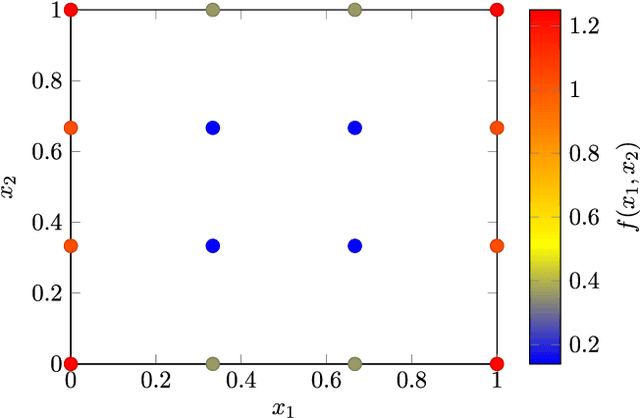
Given a data set and a subset of labels the problem of semi-supervised learning on point clouds is to extend the labels to the entire data set. In this paper we extend the labels by minimising the constrained discrete $p$-Dirichlet energy. Under suitable conditions the discrete problem can be connected, in the large data limit, with the minimiser of a weighted continuum $p$-Dirichlet energy with the same constraints. We take advantage of this connection by designing numerical schemes that first estimate the density of the data and then apply PDE methods, such as pseudo-spectral methods, to solve the corresponding Euler-Lagrange equation. We prove that our scheme is consistent in the large data limit for two methods of density estimation: kernel density estimation and spline kernel density estimation.