A Linear Transportation $\mathrm{L}^p$ Distance for Pattern Recognition

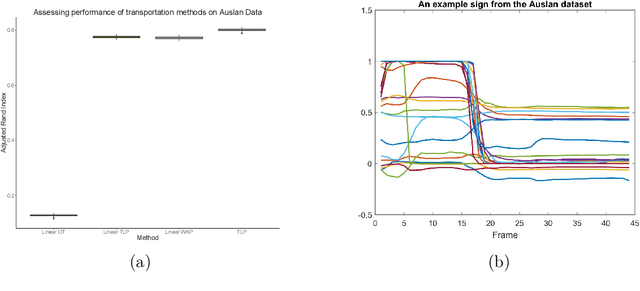
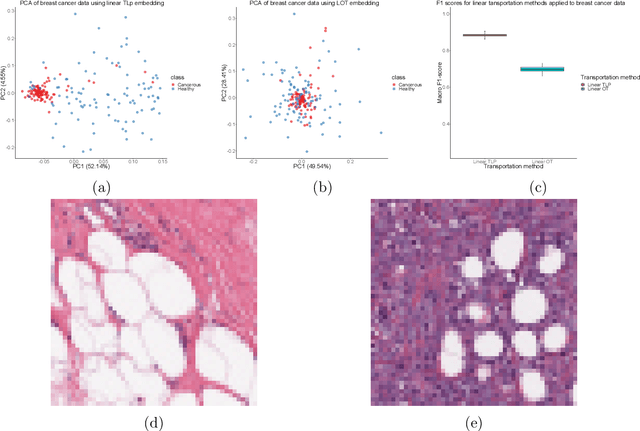
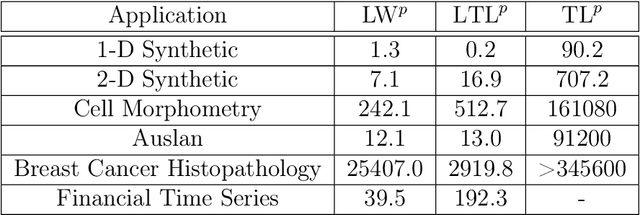
The transportation $\mathrm{L}^p$ distance, denoted $\mathrm{TL}^p$, has been proposed as a generalisation of Wasserstein $\mathrm{W}^p$ distances motivated by the property that it can be applied directly to colour or multi-channelled images, as well as multivariate time-series without normalisation or mass constraints. These distances, as with $\mathrm{W}^p$, are powerful tools in modelling data with spatial or temporal perturbations. However, their computational cost can make them infeasible to apply to even moderate pattern recognition tasks. We propose linear versions of these distances and show that the linear $\mathrm{TL}^p$ distance significantly improves over the linear $\mathrm{W}^p$ distance on signal processing tasks, whilst being several orders of magnitude faster to compute than the $\mathrm{TL}^p$ distance.

PDE-Inspired Algorithms for Semi-Supervised Learning on Point Clouds

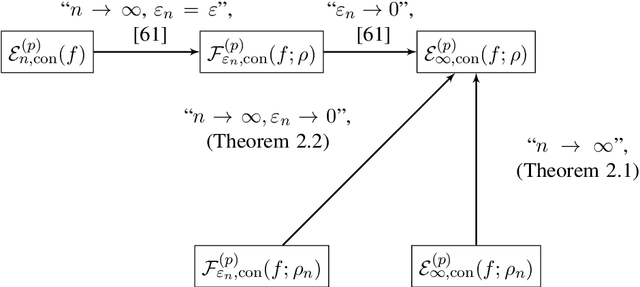
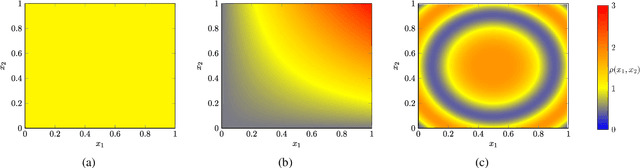
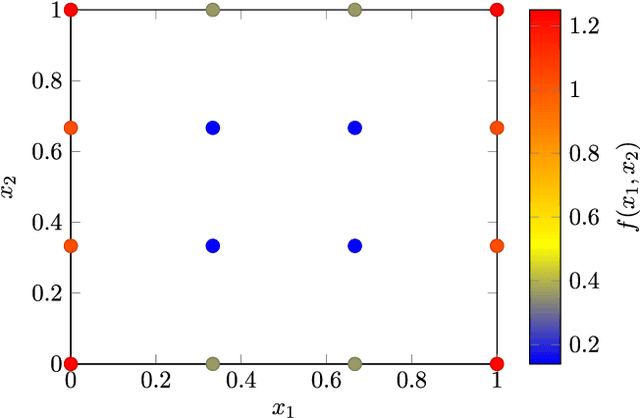
Given a data set and a subset of labels the problem of semi-supervised learning on point clouds is to extend the labels to the entire data set. In this paper we extend the labels by minimising the constrained discrete $p$-Dirichlet energy. Under suitable conditions the discrete problem can be connected, in the large data limit, with the minimiser of a weighted continuum $p$-Dirichlet energy with the same constraints. We take advantage of this connection by designing numerical schemes that first estimate the density of the data and then apply PDE methods, such as pseudo-spectral methods, to solve the corresponding Euler-Lagrange equation. We prove that our scheme is consistent in the large data limit for two methods of density estimation: kernel density estimation and spline kernel density estimation.