Bayesian Imaging With Data-Driven Priors Encoded by Neural Networks: Theory, Methods, and Algorithms
Paper and Code
Mar 18, 2021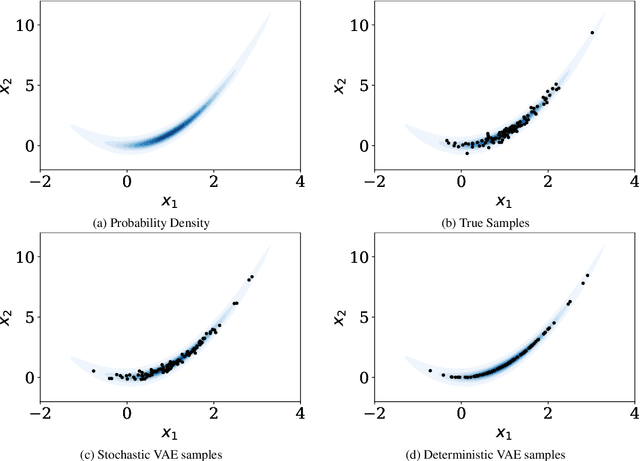

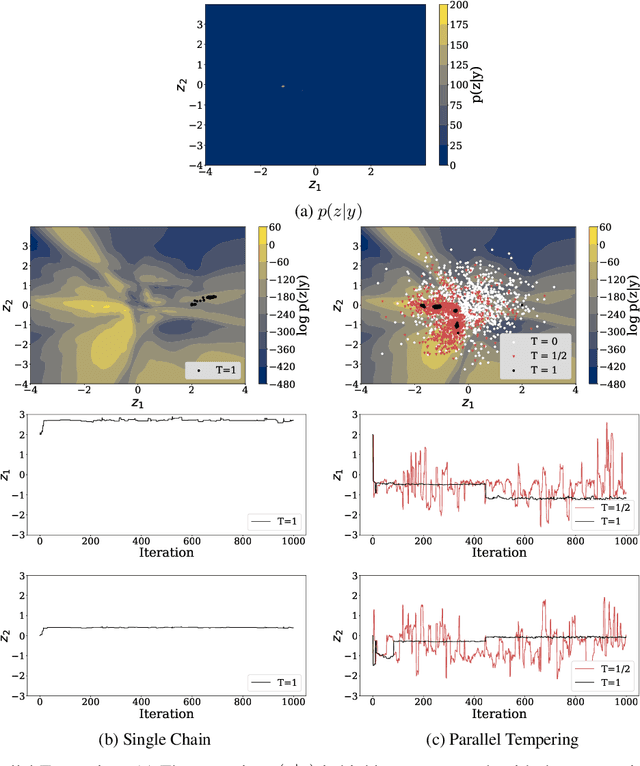
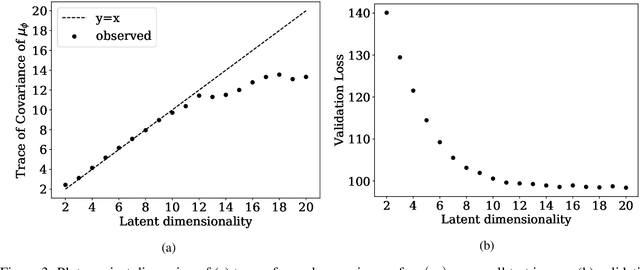
This paper proposes a new methodology for performing Bayesian inference in imaging inverse problems where the prior knowledge is available in the form of training data. Following the manifold hypothesis and adopting a generative modelling approach, we construct a data-driven prior that is supported on a sub-manifold of the ambient space, which we can learn from the training data by using a variational autoencoder or a generative adversarial network. We establish the existence and well-posedness of the associated posterior distribution and posterior moments under easily verifiable conditions, providing a rigorous underpinning for Bayesian estimators and uncertainty quantification analyses. Bayesian computation is performed by using a parallel tempered version of the preconditioned Crank-Nicolson algorithm on the manifold, which is shown to be ergodic and robust to the non-convex nature of these data-driven models. In addition to point estimators and uncertainty quantification analyses, we derive a model misspecification test to automatically detect situations where the data-driven prior is unreliable, and explain how to identify the dimension of the latent space directly from the training data. The proposed approach is illustrated with a range of experiments with the MNIST dataset, where it outperforms alternative image reconstruction approaches from the state of the art. A model accuracy analysis suggests that the Bayesian probabilities reported by the data-driven models are also remarkably accurate under a frequentist definition of probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge