Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations
Paper and Code
Apr 26, 2021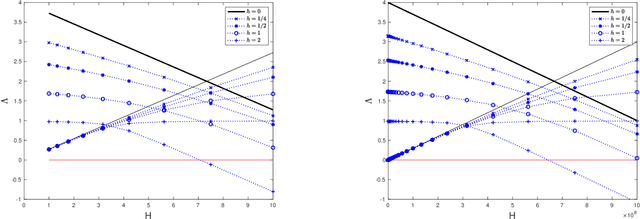
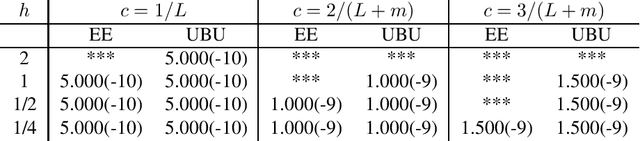
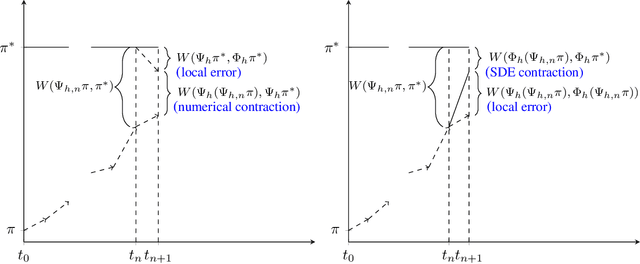
We present a framework that allows for the non-asymptotic study of the $2$-Wasserstein distance between the invariant distribution of an ergodic stochastic differential equation and the distribution of its numerical approximation in the strongly log-concave case. This allows us to study in a unified way a number of different integrators proposed in the literature for the overdamped and underdamped Langevin dynamics. In addition, we analyse a novel splitting method for the underdamped Langevin dynamics which only requires one gradient evaluation per time step. Under an additional smoothness assumption on a $d$--dimensional strongly log-concave distribution with condition number $\kappa$, the algorithm is shown to produce with an $\mathcal{O}\big(\kappa^{5/4} d^{1/4}\epsilon^{-1/2} \big)$ complexity samples from a distribution that, in Wasserstein distance, is at most $\epsilon>0$ away from the target distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge