Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations

We present a framework that allows for the non-asymptotic study of the $2$-Wasserstein distance between the invariant distribution of an ergodic stochastic differential equation and the distribution of its numerical approximation in the strongly log-concave case. This allows us to study in a unified way a number of different integrators proposed in the literature for the overdamped and underdamped Langevin dynamics. In addition, we analyse a novel splitting method for the underdamped Langevin dynamics which only requires one gradient evaluation per time step. Under an additional smoothness assumption on a $d$--dimensional strongly log-concave distribution with condition number $\kappa$, the algorithm is shown to produce with an $\mathcal{O}\big(\kappa^{5/4} d^{1/4}\epsilon^{-1/2} \big)$ complexity samples from a distribution that, in Wasserstein distance, is at most $\epsilon>0$ away from the target distribution.

The connections between Lyapunov functions for some optimization algorithms and differential equations

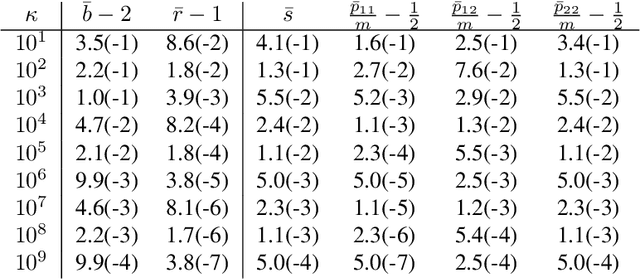
In this manuscript we study the properties of a family of a second order differential equations with damping, its discretizations and their connections with accelerated optimization algorithms for $m$-strongly convex and $L$-smooth functions. In particular, using the Linear Matrix Inequality framework developed in \emph{Fazlyab et. al. $(2018)$}, we derive analytically a (discrete) Lyapunov function for a two-parameter family of Nesterov optimization methods, which allows for a complete characterization of their convergence rate. We then show that in the appropriate limit this family of methods may be seen as a discretization of a family of second order ordinary differential equations, which properties can be also understood by a (continuous) Lyapunov function, which can also be obtained by studying the limiting behaviour of the discrete Lyapunov function. Finally, we show that the majority of typical discretizations of this ODE, such as the Heavy ball method, do not possess suitable discrete Lyapunov functions, and hence fail to reproduce the desired limiting behaviour of this ODE, which in turn implies that their converge rates when seen as optimization methods cannot behave in an "accerelated" manner .