Reconstruction of Manifold Distances from Noisy Observations

We consider the problem of reconstructing the intrinsic geometry of a manifold from noisy pairwise distance observations. Specifically, let $M$ denote a diameter 1 d-dimensional manifold and $μ$ a probability measure on $M$ that is mutually absolutely continuous with the volume measure. Suppose $X_1,\dots,X_N$ are i.i.d. samples of $μ$ and we observe noisy-distance random variables $d'(X_j, X_k)$ that are related to the true geodesic distances $d(X_j,X_k)$. With mild assumptions on the distributions and independence of the noisy distances, we develop a new framework for recovering all distances between points in a sufficiently dense subsample of $M$. Our framework improves on previous work which assumed i.i.d. additive noise with known moments. Our method is based on a new way to estimate $L_2$-norms of certain expectation-functions $f_x(y)=\mathbb{E}d'(x,y)$ and use them to build robust clusters centered at points of our sample. Using a new geometric argument, we establish that, under mild geometric assumptions--bounded curvature and positive injectivity radius--these clusters allow one to recover the true distances between points in the sample up to an additive error of $O(\varepsilon \log \varepsilon^{-1})$. We develop two distinct algorithms for producing these clusters. The first achieves a sample complexity $N \asymp \varepsilon^{-2d-2}\log(1/\varepsilon)$ and runtime $o(N^3)$. The second introduces novel geometric ideas that warrant further investigation. In the presence of missing observations, we show that a quantitative lower bound on sampling probabilities suffices to modify the cluster construction in the first algorithm and extend all recovery guarantees. Our main technical result also elucidates which properties of a manifold are necessary for the distance recovery, which suggests further extension of our techniques to a broader class of metric probability spaces.

Predicting Language Models' Success at Zero-Shot Probabilistic Prediction

Recent work has investigated the capabilities of large language models (LLMs) as zero-shot models for generating individual-level characteristics (e.g., to serve as risk models or augment survey datasets). However, when should a user have confidence that an LLM will provide high-quality predictions for their particular task? To address this question, we conduct a large-scale empirical study of LLMs' zero-shot predictive capabilities across a wide range of tabular prediction tasks. We find that LLMs' performance is highly variable, both on tasks within the same dataset and across different datasets. However, when the LLM performs well on the base prediction task, its predicted probabilities become a stronger signal for individual-level accuracy. Then, we construct metrics to predict LLMs' performance at the task level, aiming to distinguish between tasks where LLMs may perform well and where they are likely unsuitable. We find that some of these metrics, each of which are assessed without labeled data, yield strong signals of LLMs' predictive performance on new tasks.

Work Smarter Not Harder: Simple Imitation Learning with CS-PIBT Outperforms Large Scale Imitation Learning for MAPF

Multi-Agent Path Finding (MAPF) is the problem of effectively finding efficient collision-free paths for a group of agents in a shared workspace. The MAPF community has largely focused on developing high-performance heuristic search methods. Recently, several works have applied various machine learning (ML) techniques to solve MAPF, usually involving sophisticated architectures, reinforcement learning techniques, and set-ups, but none using large amounts of high-quality supervised data. Our initial objective in this work was to show how simple large scale imitation learning of high-quality heuristic search methods can lead to state-of-the-art ML MAPF performance. However, we find that, at least with our model architecture, simple large scale (700k examples with hundreds of agents per example) imitation learning does \textit{not} produce impressive results. Instead, we find that by using prior work that post-processes MAPF model predictions to resolve 1-step collisions (CS-PIBT), we can train a simple ML MAPF model in minutes that dramatically outperforms existing ML MAPF policies. This has serious implications for all future ML MAPF policies (with local communication) which currently struggle to scale. In particular, this finding implies that future learnt policies should (1) always use smart 1-step collision shields (e.g. CS-PIBT), (2) always include the collision shield with greedy actions as a baseline (e.g. PIBT) and (3) motivates future models to focus on longer horizon / more complex planning as 1-step collisions can be efficiently resolved.

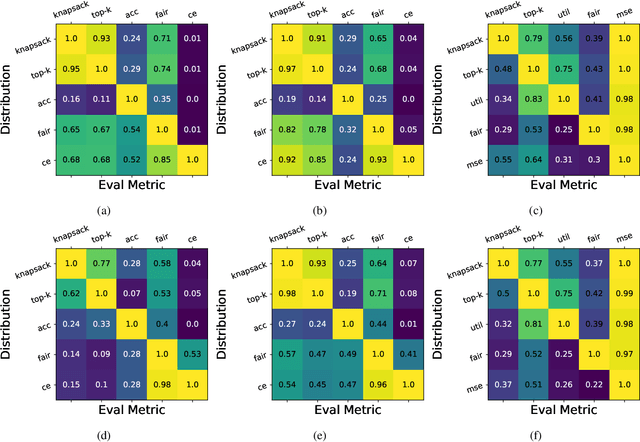
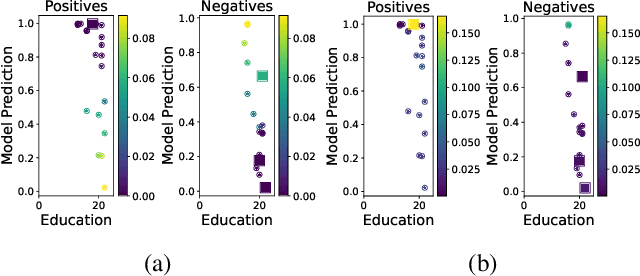
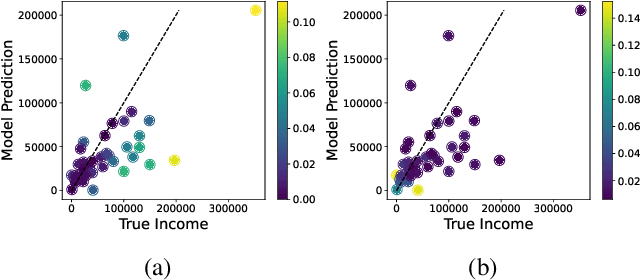
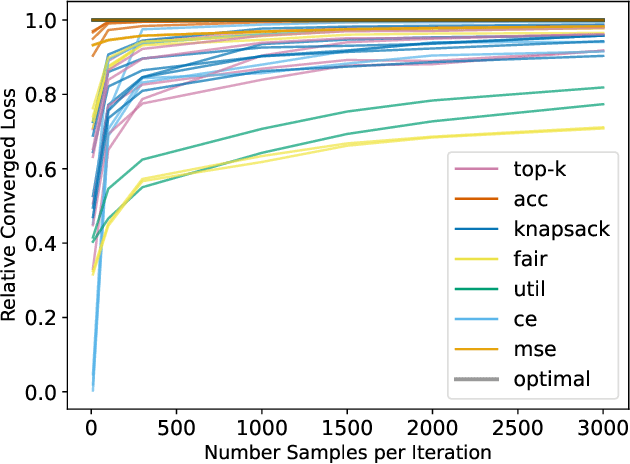
Decision-Focused Evaluation of Worst-Case Distribution Shift

Distribution shift is a key challenge for predictive models in practice, creating the need to identify potentially harmful shifts in advance of deployment. Existing work typically defines these worst-case shifts as ones that most degrade the individual-level accuracy of the model. However, when models are used to make a downstream population-level decision like the allocation of a scarce resource, individual-level accuracy may be a poor proxy for performance on the task at hand. We introduce a novel framework that employs a hierarchical model structure to identify worst-case distribution shifts in predictive resource allocation settings by capturing shifts both within and across instances of the decision problem. This task is more difficult than in standard distribution shift settings due to combinatorial interactions, where decisions depend on the joint presence of individuals in the allocation task. We show that the problem can be reformulated as a submodular optimization problem, enabling efficient approximations of worst-case loss. Applying our framework to real data, we find empirical evidence that worst-case shifts identified by one metric often significantly diverge from worst-case distributions identified by other metrics.

Improving Learnt Local MAPF Policies with Heuristic Search

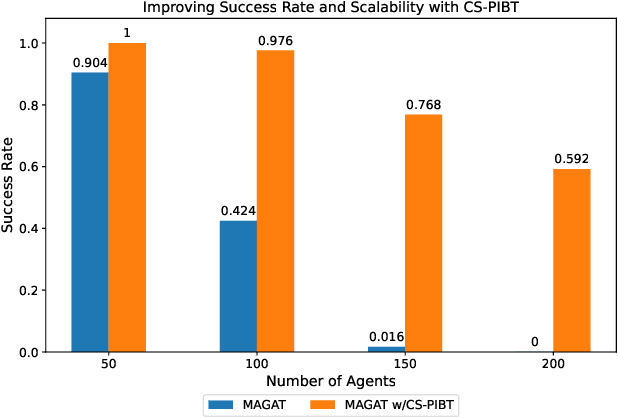
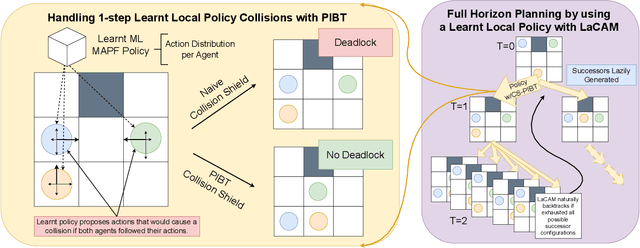
Multi-agent path finding (MAPF) is the problem of finding collision-free paths for a team of agents to reach their goal locations. State-of-the-art classical MAPF solvers typically employ heuristic search to find solutions for hundreds of agents but are typically centralized and can struggle to scale when run with short timeouts. Machine learning (ML) approaches that learn policies for each agent are appealing as these could enable decentralized systems and scale well while maintaining good solution quality. Current ML approaches to MAPF have proposed methods that have started to scratch the surface of this potential. However, state-of-the-art ML approaches produce "local" policies that only plan for a single timestep and have poor success rates and scalability. Our main idea is that we can improve a ML local policy by using heuristic search methods on the output probability distribution to resolve deadlocks and enable full horizon planning. We show several model-agnostic ways to use heuristic search with learnt policies that significantly improve the policies' success rates and scalability. To our best knowledge, we demonstrate the first time ML-based MAPF approaches have scaled to high congestion scenarios (e.g. 20% agent density).