Decision-Focused Uncertainty Quantification

There is increasing interest in ''decision-focused'' machine learning methods which train models to account for how their predictions are used in downstream optimization problems. Doing so can often improve performance on subsequent decision problems. However, current methods for uncertainty quantification do not incorporate any information at all about downstream decisions. We develop a framework based on conformal prediction to produce prediction sets that account for a downstream decision loss function, making them more appropriate to inform high-stakes decision-making. Our approach harnesses the strengths of conformal methods--modularity, model-agnosticism, and statistical coverage guarantees--while incorporating downstream decisions and user-specified utility functions. We prove that our methods retain standard coverage guarantees. Empirical evaluation across a range of datasets and utility metrics demonstrates that our methods achieve significantly lower decision loss compared to standard conformal methods. Additionally, we present a real-world use case in healthcare diagnosis, where our method effectively incorporates the hierarchical structure of dermatological diseases. It successfully generates sets with coherent diagnostic meaning, aiding the triage process during dermatology diagnosis and illustrating how our method can ground high-stakes decision-making on external domain knowledge.

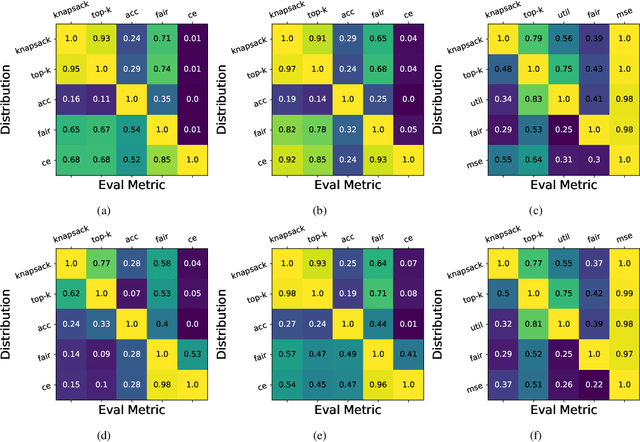
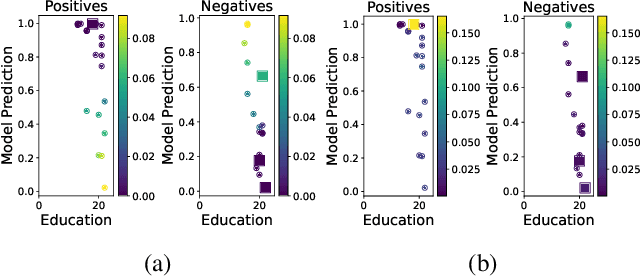
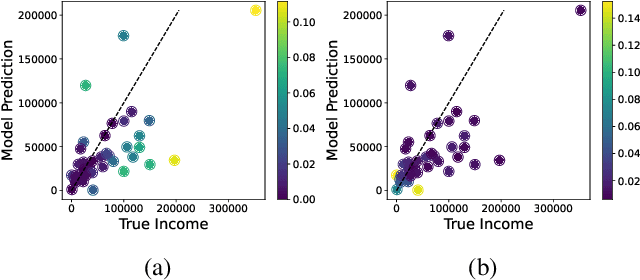
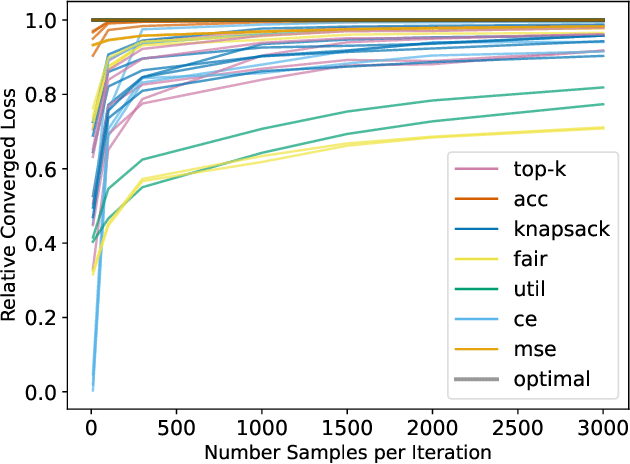
Decision-Focused Evaluation of Worst-Case Distribution Shift

Distribution shift is a key challenge for predictive models in practice, creating the need to identify potentially harmful shifts in advance of deployment. Existing work typically defines these worst-case shifts as ones that most degrade the individual-level accuracy of the model. However, when models are used to make a downstream population-level decision like the allocation of a scarce resource, individual-level accuracy may be a poor proxy for performance on the task at hand. We introduce a novel framework that employs a hierarchical model structure to identify worst-case distribution shifts in predictive resource allocation settings by capturing shifts both within and across instances of the decision problem. This task is more difficult than in standard distribution shift settings due to combinatorial interactions, where decisions depend on the joint presence of individuals in the allocation task. We show that the problem can be reformulated as a submodular optimization problem, enabling efficient approximations of worst-case loss. Applying our framework to real data, we find empirical evidence that worst-case shifts identified by one metric often significantly diverge from worst-case distributions identified by other metrics.

Auditing Fairness under Unobserved Confounding

A fundamental problem in decision-making systems is the presence of inequity across demographic lines. However, inequity can be difficult to quantify, particularly if our notion of equity relies on hard-to-measure notions like risk (e.g., equal access to treatment for those who would die without it). Auditing such inequity requires accurate measurements of individual risk, which is difficult to estimate in the realistic setting of unobserved confounding. In the case that these unobservables "explain" an apparent disparity, we may understate or overstate inequity. In this paper, we show that one can still give informative bounds on allocation rates among high-risk individuals, even while relaxing or (surprisingly) even when eliminating the assumption that all relevant risk factors are observed. We utilize the fact that in many real-world settings (e.g., the introduction of a novel treatment) we have data from a period prior to any allocation, to derive unbiased estimates of risk. We demonstrate the effectiveness of our framework on a real-world study of Paxlovid allocation to COVID-19 patients, finding that observed racial inequity cannot be explained by unobserved confounders of the same strength as important observed covariates.

Bayesian Neural Networks with Domain Knowledge Priors

Bayesian neural networks (BNNs) have recently gained popularity due to their ability to quantify model uncertainty. However, specifying a prior for BNNs that captures relevant domain knowledge is often extremely challenging. In this work, we propose a framework for integrating general forms of domain knowledge (i.e., any knowledge that can be represented by a loss function) into a BNN prior through variational inference, while enabling computationally efficient posterior inference and sampling. Specifically, our approach results in a prior over neural network weights that assigns high probability mass to models that better align with our domain knowledge, leading to posterior samples that also exhibit this behavior. We show that BNNs using our proposed domain knowledge priors outperform those with standard priors (e.g., isotropic Gaussian, Gaussian process), successfully incorporating diverse types of prior information such as fairness, physics rules, and healthcare knowledge and achieving better predictive performance. We also present techniques for transferring the learned priors across different model architectures, demonstrating their broad utility across various settings.