CEHR-GPT: Generating Electronic Health Records with Chronological Patient Timelines

Synthetic Electronic Health Records (EHR) have emerged as a pivotal tool in advancing healthcare applications and machine learning models, particularly for researchers without direct access to healthcare data. Although existing methods, like rule-based approaches and generative adversarial networks (GANs), generate synthetic data that resembles real-world EHR data, these methods often use a tabular format, disregarding temporal dependencies in patient histories and limiting data replication. Recently, there has been a growing interest in leveraging Generative Pre-trained Transformers (GPT) for EHR data. This enables applications like disease progression analysis, population estimation, counterfactual reasoning, and synthetic data generation. In this work, we focus on synthetic data generation and demonstrate the capability of training a GPT model using a particular patient representation derived from CEHR-BERT, enabling us to generate patient sequences that can be seamlessly converted to the Observational Medical Outcomes Partnership (OMOP) data format.

The Limit of the Marginal Distribution Model in Consumer Choice

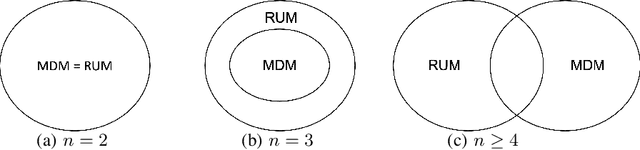
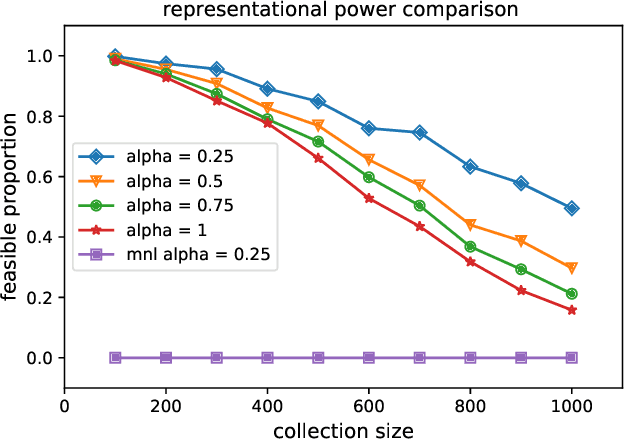
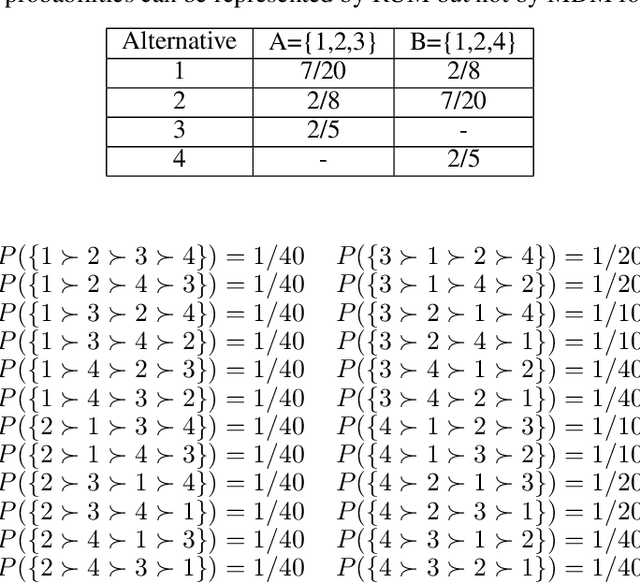
Given data on choices made by consumers for different assortments, a key challenge is to develop parsimonious models that describe and predict consumer choice behavior. One such choice model is the marginal distribution model which requires only the specification of the marginal distributions of the random utilities of the alternatives to explain choice data. In this paper, we develop an exact characterisation of the set of choice probabilities which are representable by the marginal distribution model consistently across any collection of assortments. Allowing for the possibility of alternatives to be grouped based on the marginal distribution of their utilities, we show (a) verifying consistency of choice probability data with this model is possible in polynomial time and (b) finding the closest fit reduces to solving a mixed integer convex program. Our results show that the marginal distribution model provides much better representational power as compared to multinomial logit and much better computational performance as compared to the random utility model.

Discrete Optimal Transport with Independent Marginals is #P-Hard

We study the computational complexity of the optimal transport problem that evaluates the Wasserstein distance between the distributions of two K-dimensional discrete random vectors. The best known algorithms for this problem run in polynomial time in the maximum of the number of atoms of the two distributions. However, if the components of either random vector are independent, then this number can be exponential in K even though the size of the problem description scales linearly with K. We prove that the described optimal transport problem is #P-hard even if all components of the first random vector are independent uniform Bernoulli random variables, while the second random vector has merely two atoms, and even if only approximate solutions are sought. We also develop a dynamic programming-type algorithm that approximates the Wasserstein distance in pseudo-polynomial time when the components of the first random vector follow arbitrary independent discrete distributions, and we identify special problem instances that can be solved exactly in strongly polynomial time.

CEHR-BERT: Incorporating temporal information from structured EHR data to improve prediction tasks

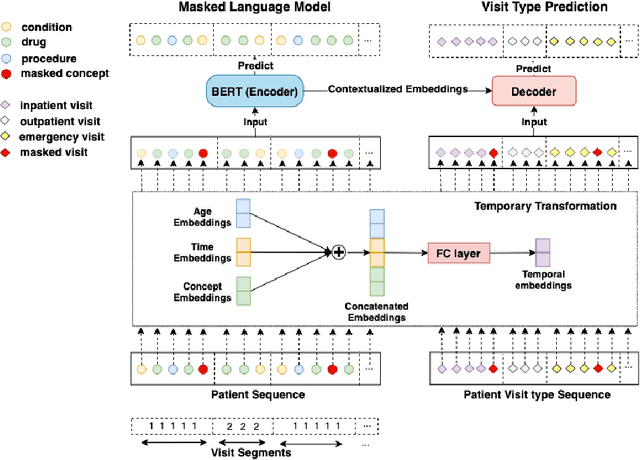
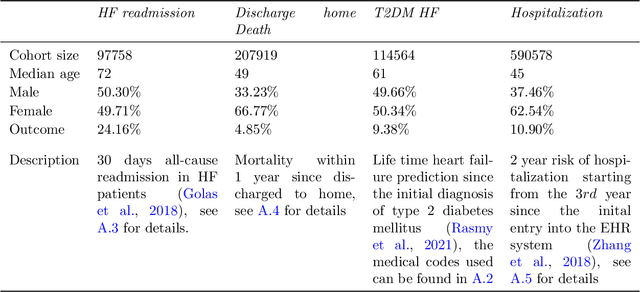
Embedding algorithms are increasingly used to represent clinical concepts in healthcare for improving machine learning tasks such as clinical phenotyping and disease prediction. Recent studies have adapted state-of-the-art bidirectional encoder representations from transformers (BERT) architecture to structured electronic health records (EHR) data for the generation of contextualized concept embeddings, yet do not fully incorporate temporal data across multiple clinical domains. Therefore we developed a new BERT adaptation, CEHR-BERT, to incorporate temporal information using a hybrid approach by augmenting the input to BERT using artificial time tokens, incorporating time, age, and concept embeddings, and introducing a new second learning objective for visit type. CEHR-BERT was trained on a subset of Columbia University Irving Medical Center-York Presbyterian Hospital's clinical data, which includes 2.4M patients, spanning over three decades, and tested using 4-fold cross-validation on the following prediction tasks: hospitalization, death, new heart failure (HF) diagnosis, and HF readmission. Our experiments show that CEHR-BERT outperformed existing state-of-the-art clinical BERT adaptations and baseline models across all 4 prediction tasks in both ROC-AUC and PR-AUC. CEHR-BERT also demonstrated strong transfer learning capability, as our model trained on only 5% of data outperformed comparison models trained on the entire data set. Ablation studies to better understand the contribution of each time component showed incremental gains with every element, suggesting that CEHR-BERT's incorporation of artificial time tokens, time and age embeddings with concept embeddings, and the addition of the second learning objective represents a promising approach for future BERT-based clinical embeddings.

Correlation Robust Influence Maximization

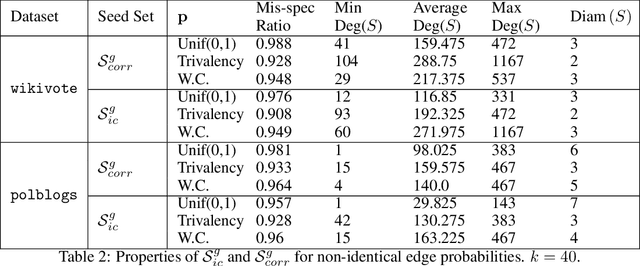
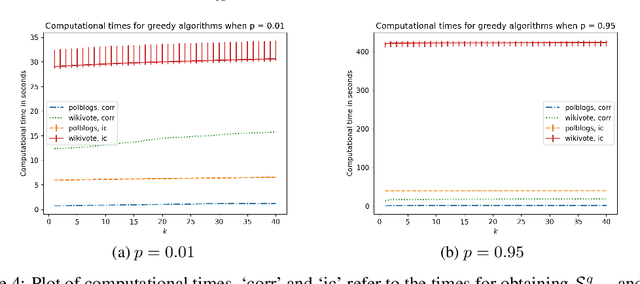
We propose a distributionally robust model for the influence maximization problem. Unlike the classic independent cascade model \citep{kempe2003maximizing}, this model's diffusion process is adversarially adapted to the choice of seed set. Hence, instead of optimizing under the assumption that all influence relationships in the network are independent, we seek a seed set whose expected influence under the worst correlation, i.e. the "worst-case, expected influence", is maximized. We show that this worst-case influence can be efficiently computed, and though the optimization is NP-hard, a ($1 - 1/e$) approximation guarantee holds. We also analyze the structure to the adversary's choice of diffusion process, and contrast with established models. Beyond the key computational advantages, we also highlight the extent to which the independence assumption may cost optimality, and provide insights from numerical experiments comparing the adversarial and independent cascade model.