Chee Chin Lim
Correlation Robust Influence Maximization
Oct 24, 2020
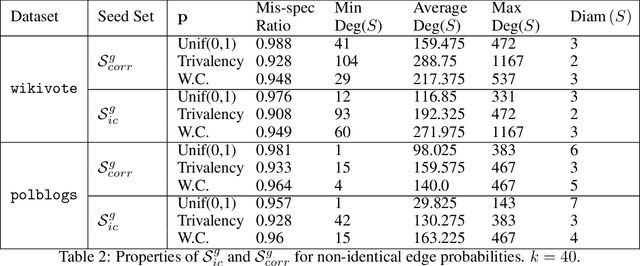
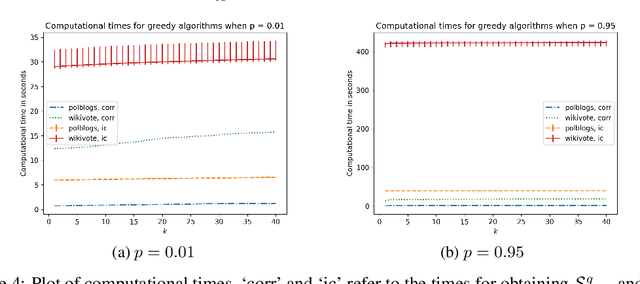

Abstract:We propose a distributionally robust model for the influence maximization problem. Unlike the classic independent cascade model \citep{kempe2003maximizing}, this model's diffusion process is adversarially adapted to the choice of seed set. Hence, instead of optimizing under the assumption that all influence relationships in the network are independent, we seek a seed set whose expected influence under the worst correlation, i.e. the "worst-case, expected influence", is maximized. We show that this worst-case influence can be efficiently computed, and though the optimization is NP-hard, a ($1 - 1/e$) approximation guarantee holds. We also analyze the structure to the adversary's choice of diffusion process, and contrast with established models. Beyond the key computational advantages, we also highlight the extent to which the independence assumption may cost optimality, and provide insights from numerical experiments comparing the adversarial and independent cascade model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge