Trajectory PMB Filters for Extended Object Tracking Using Belief Propagation

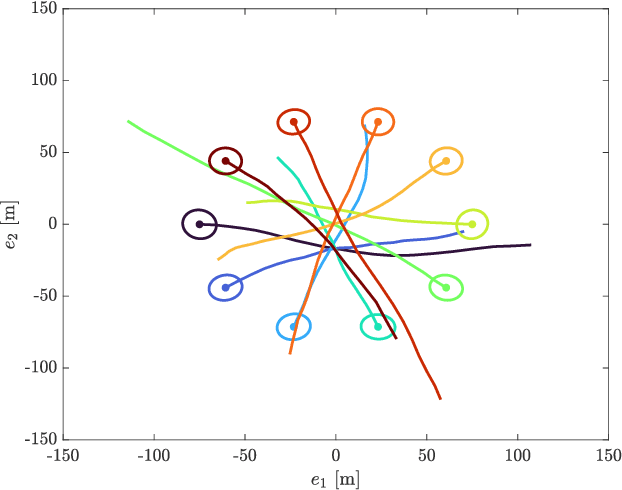
In this paper, we propose a Poisson multi-Bernoulli (PMB) filter for extended object tracking (EOT), which directly estimates the set of object trajectories, using belief propagation (BP). The proposed filter propagates a PMB density on the posterior of sets of trajectories through the filtering recursions over time, where the PMB mixture (PMBM) posterior after the update step is approximated as a PMB. The efficient PMB approximation relies on several important theoretical contributions. First, we present a PMBM conjugate prior on the posterior of sets of trajectories for a generalized measurement model, in which each object generates an independent set of measurements. The PMBM density is a conjugate prior in the sense that both the prediction and the update steps preserve the PMBM form of the density. Second, we present a factor graph representation of the joint posterior of the PMBM set of trajectories and association variables for the Poisson spatial measurement model. Importantly, leveraging the PMBM conjugacy and the factor graph formulation enables an elegant treatment on undetected objects via a Poisson point process and efficient inference on sets of trajectories using BP, where the approximate marginal densities in the PMB approximation can be obtained without enumeration of different data association hypotheses. To achieve this, we present a particle-based implementation of the proposed filter, where smoothed trajectory estimates, if desired, can be obtained via single-object particle smoothing methods, and its performance for EOT with ellipsoidal shapes is evaluated in a simulation study.

Multiple Object Trajectory Estimation Using Backward Simulation

This paper presents a general solution for computing the multi-object posterior for sets of trajectories from a sequence of multi-object (unlabelled) filtering densities and a multi-object dynamic model. Importantly, the proposed solution opens an avenue of trajectory estimation possibilities for multi-object filters that do not explicitly estimate trajectories. In this paper, we first derive a general multi-trajectory backward smoothing equation based on random finite sets of trajectories. Then we show how to sample sets of trajectories using backward simulation for Poisson multi-Bernoulli filtering densities, and develop a tractable implementation based on ranked assignment. The performance of the resulting multi-trajectory particle smoothers is evaluated in a simulation study, and the results demonstrate that they have superior performance in comparison to several state-of-the-art multi-object filters and smoothers.

PMBM-based SLAM Filters in 5G mmWave Vehicular Networks

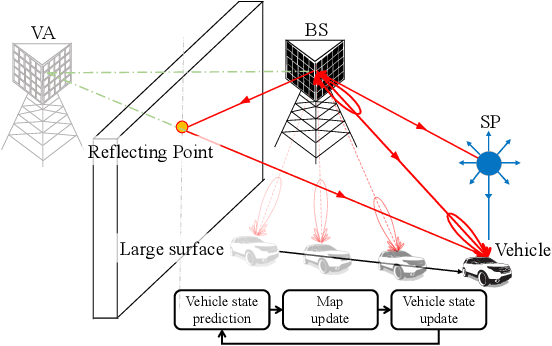
Radio-based vehicular simultaneous localization and mapping (SLAM) aims to localize vehicles while mapping the landmarks in the environment. We propose a sequence of three Poisson multi-Bernoulli mixture (PMBM) based SLAM filters, which handle the entire SLAM problem in a theoretically optimal manner. The complexity of the three proposed SLAM filters is progressively reduced while sustaining high accuracy by deriving SLAM density approximation with the marginalization of nuisance parameters (either vehicle state or data association). Firstly, the PMBM SLAM filter serves as the foundation, for which we provide the first complete description based on a Rao-Blackwellized particle filter. Secondly, the Poisson multi-Bernoulli (PMB) SLAM filter is based on the standard reduction from PMBM to PMB, but involves a novel interpretation based on auxiliary variables and a relation to Bethe free energy. Finally, using the same auxiliary variable argument, we derive a marginalized PMB SLAM filter, which avoids particles and is instead implemented with a low-complexity cubature Kalman filter. We evaluate the three proposed SLAM filters in comparison with the probability hypothesis density (PHD) SLAM filter in 5G mmWave vehicular networks and show the computation-performance trade-off between them.

Trajectory Poisson multi-Bernoulli filters

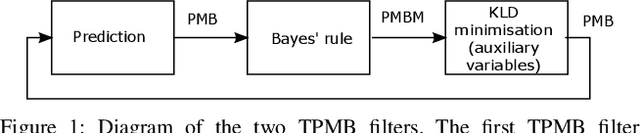
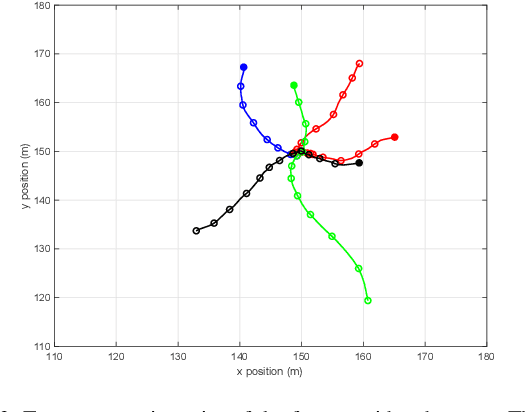
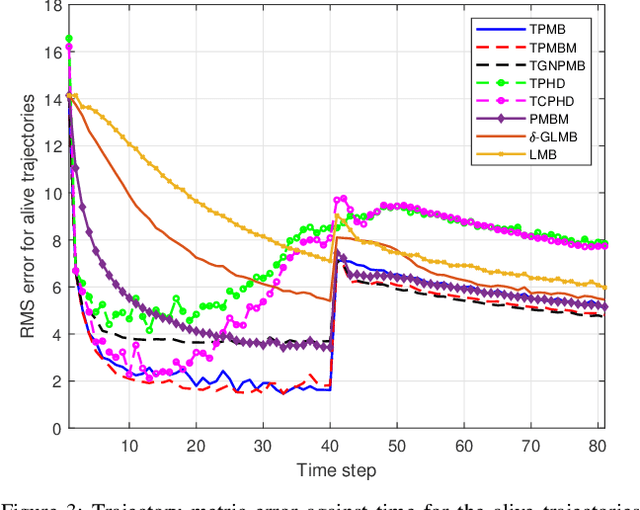
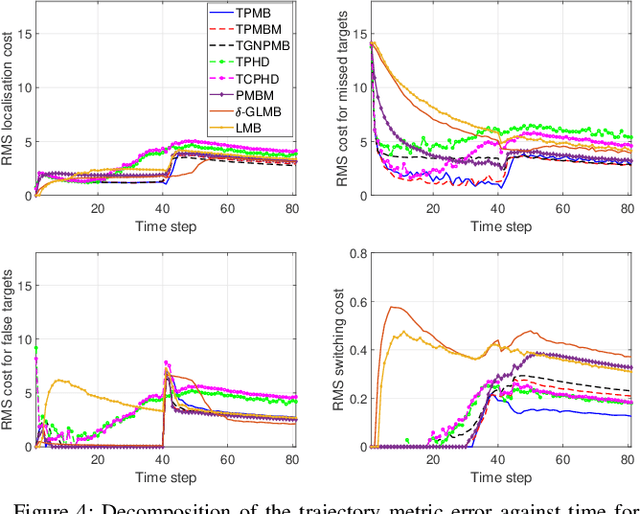
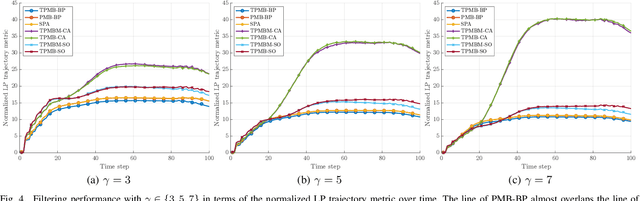
This paper presents two trajectory Poisson multi-Bernoulli (TPMB) filters for multi-target tracking: one to estimate the set of alive trajectories at each time step and another to estimate the set of all trajectories, which includes alive and dead trajectories, at each time step. The filters are based on propagating a Poisson multi-Bernoulli (PMB) density on the corresponding set of trajectories through the filtering recursion. After the update step, the posterior is a PMB mixture (PMBM) so, in order to obtain a PMB density, a Kullback-Leibler divergence minimisation on an augmented space is performed. The developed filters are computationally lighter alternatives to the trajectory PMBM filters, which provide the closed-form recursion for sets of trajectories with Poisson birth model, and are shown to outperform previous multi-target tracking algorithms.

Poisson Multi-Bernoulli Mixtures for Sets of Trajectories

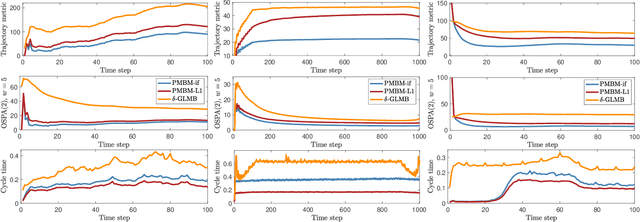
For the standard point target model with Poisson birth process, the Poisson Multi-Bernoulli Mixture (PMBM) is a conjugate multi-target density. The PMBM filter for sets of targets has been shown to have state-of-the-art performance and a structure similar to the Multiple Hypothesis Tracker (MHT). In this paper we consider a recently developed formulation of multiple target tracking as a random finite set (RFS) of trajectories, and present three important and interesting results. First, we show that, for the standard point target model, the PMBM density is conjugate also for sets of trajectories. Second, based on this we develop PMBM trackers (trajectory RFS filters) that efficiently estimate the set of trajectories. Third, we establish that for the standard point target model the multi-trajectory density is PMBM for trajectories in any time window, given measurements in any (possibly non-overlapping) time window. In addition, the PMBM trackers are evaluated in a simulation study, and shown to yield state-of-the-art performance.

Gaussian implementation of the multi-Bernoulli mixture filter

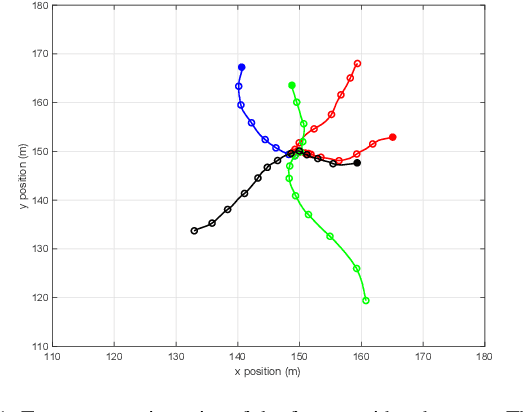
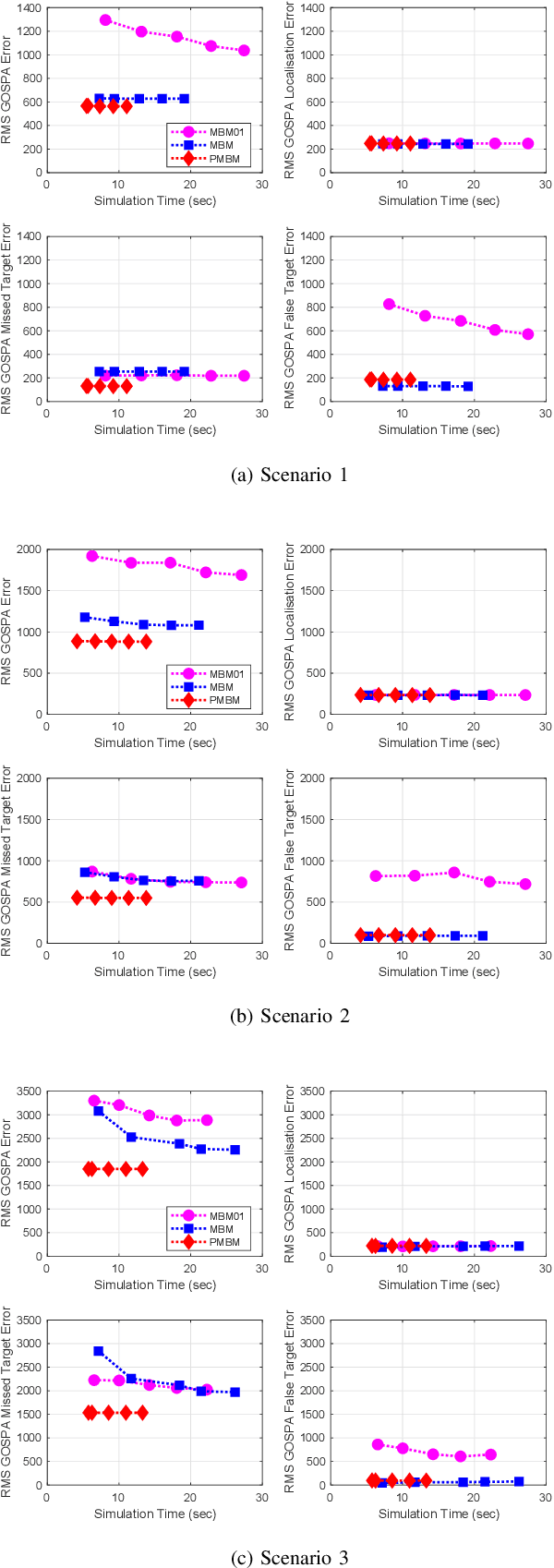
This paper presents the Gaussian implementation of the multi-Bernoulli mixture (MBM) filter. The MBM filter provides the filtering (multi-target) density for the standard dynamic and radar measurement models when the birth model is multi-Bernoulli or multi-Bernoulli mixture. Under linear/Gaussian models, the single target densities of the MBM mixture admit Gaussian closed-form expressions. Murty's algorithm is used to select the global hypotheses with highest weights. The MBM filter is compared with other algorithms in the literature via numerical simulations.

Poisson Multi-Bernoulli Mapping Using Gibbs Sampling

This paper addresses the mapping problem. Using a conjugate prior form, we derive the exact theoretical batch multi-object posterior density of the map given a set of measurements. The landmarks in the map are modeled as extended objects, and the measurements are described as a Poisson process, conditioned on the map. We use a Poisson process prior on the map and prove that the posterior distribution is a hybrid Poisson, multi-Bernoulli mixture distribution. We devise a Gibbs sampling algorithm to sample from the batch multi-object posterior. The proposed method can handle uncertainties in the data associations and the cardinality of the set of landmarks, and is parallelizable, making it suitable for large-scale problems. The performance of the proposed method is evaluated on synthetic data and is shown to outperform a state-of-the-art method.

Poisson multi-Bernoulli mixture filter: direct derivation and implementation

We provide a derivation of the Poisson multi-Bernoulli mixture (PMBM) filter for multi-target tracking with the standard point target measurements without using probability generating functionals or functional derivatives. We also establish the connection with the \delta-generalised labelled multi-Bernoulli (\delta-GLMB) filter, showing that a \delta-GLMB density represents a multi-Bernoulli mixture with labelled targets so it can be seen as a special case of PMBM. In addition, we propose an implementation for linear/Gaussian dynamic and measurement models and how to efficiently obtain typical estimators in the literature from the PMBM. The PMBM filter is shown to outperform other filters in the literature in a challenging scenario.