SplatAD: Real-Time Lidar and Camera Rendering with 3D Gaussian Splatting for Autonomous Driving

Ensuring the safety of autonomous robots, such as self-driving vehicles, requires extensive testing across diverse driving scenarios. Simulation is a key ingredient for conducting such testing in a cost-effective and scalable way. Neural rendering methods have gained popularity, as they can build simulation environments from collected logs in a data-driven manner. However, existing neural radiance field (NeRF) methods for sensor-realistic rendering of camera and lidar data suffer from low rendering speeds, limiting their applicability for large-scale testing. While 3D Gaussian Splatting (3DGS) enables real-time rendering, current methods are limited to camera data and are unable to render lidar data essential for autonomous driving. To address these limitations, we propose SplatAD, the first 3DGS-based method for realistic, real-time rendering of dynamic scenes for both camera and lidar data. SplatAD accurately models key sensor-specific phenomena such as rolling shutter effects, lidar intensity, and lidar ray dropouts, using purpose-built algorithms to optimize rendering efficiency. Evaluation across three autonomous driving datasets demonstrates that SplatAD achieves state-of-the-art rendering quality with up to +2 PSNR for NVS and +3 PSNR for reconstruction while increasing rendering speed over NeRF-based methods by an order of magnitude. See https://research.zenseact.com/publications/splatad/ for our project page.

Are NeRFs ready for autonomous driving? Towards closing the real-to-simulation gap

Neural Radiance Fields (NeRFs) have emerged as promising tools for advancing autonomous driving (AD) research, offering scalable closed-loop simulation and data augmentation capabilities. However, to trust the results achieved in simulation, one needs to ensure that AD systems perceive real and rendered data in the same way. Although the performance of rendering methods is increasing, many scenarios will remain inherently challenging to reconstruct faithfully. To this end, we propose a novel perspective for addressing the real-to-simulated data gap. Rather than solely focusing on improving rendering fidelity, we explore simple yet effective methods to enhance perception model robustness to NeRF artifacts without compromising performance on real data. Moreover, we conduct the first large-scale investigation into the real-to-simulated data gap in an AD setting using a state-of-the-art neural rendering technique. Specifically, we evaluate object detectors and an online mapping model on real and simulated data, and study the effects of different pre-training strategies. Our results show notable improvements in model robustness to simulated data, even improving real-world performance in some cases. Last, we delve into the correlation between the real-to-simulated gap and image reconstruction metrics, identifying FID and LPIPS as strong indicators.

Poisson Multi-Bernoulli Mapping Using Gibbs Sampling

This paper addresses the mapping problem. Using a conjugate prior form, we derive the exact theoretical batch multi-object posterior density of the map given a set of measurements. The landmarks in the map are modeled as extended objects, and the measurements are described as a Poisson process, conditioned on the map. We use a Poisson process prior on the map and prove that the posterior distribution is a hybrid Poisson, multi-Bernoulli mixture distribution. We devise a Gibbs sampling algorithm to sample from the batch multi-object posterior. The proposed method can handle uncertainties in the data associations and the cardinality of the set of landmarks, and is parallelizable, making it suitable for large-scale problems. The performance of the proposed method is evaluated on synthetic data and is shown to outperform a state-of-the-art method.

Poisson multi-Bernoulli conjugate prior for multiple extended object estimation

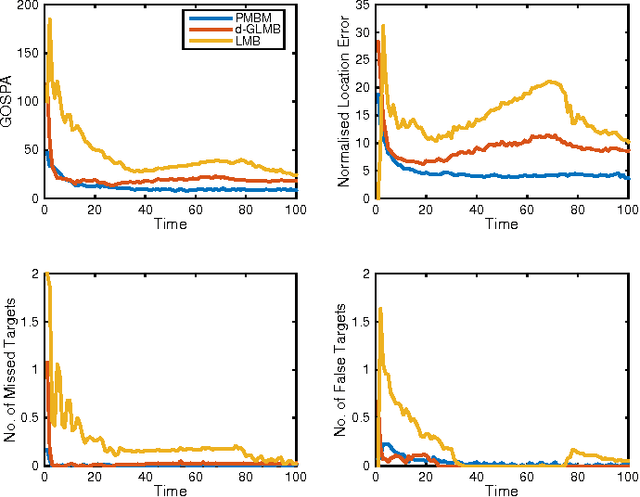
This paper presents a Poisson multi-Bernoulli mixture (PMBM) conjugate prior for multiple extended object filtering. A Poisson point process is used to describe the existence of yet undetected targets, while a multi-Bernoulli mixture describes the distribution of the targets that have been detected. The prediction and update equations are presented for the standard transition density and measurement likelihood. Both the prediction and the update preserve the PMBM form of the density, and in this sense the PMBM density is a conjugate prior. However, the unknown data associations lead to an intractably large number of terms in the PMBM density, and approximations are necessary for tractability. A gamma Gaussian inverse Wishart implementation is presented, along with methods to handle the data association problem. A simulation study shows that the extended target PMBM filter outperforms the extended target $\delta$-GLMB and LMB filters. An experiment with Lidar data illustrates the benefit of tracking both detected and undetected targets.