Poisson Multi-Bernoulli Mixtures for Sets of Trajectories
Paper and Code
Dec 17, 2019
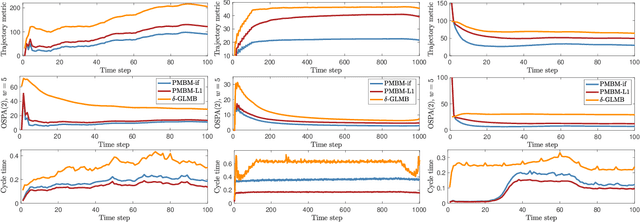


For the standard point target model with Poisson birth process, the Poisson Multi-Bernoulli Mixture (PMBM) is a conjugate multi-target density. The PMBM filter for sets of targets has been shown to have state-of-the-art performance and a structure similar to the Multiple Hypothesis Tracker (MHT). In this paper we consider a recently developed formulation of multiple target tracking as a random finite set (RFS) of trajectories, and present three important and interesting results. First, we show that, for the standard point target model, the PMBM density is conjugate also for sets of trajectories. Second, based on this we develop PMBM trackers (trajectory RFS filters) that efficiently estimate the set of trajectories. Third, we establish that for the standard point target model the multi-trajectory density is PMBM for trajectories in any time window, given measurements in any (possibly non-overlapping) time window. In addition, the PMBM trackers are evaluated in a simulation study, and shown to yield state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge