PMBM-based SLAM Filters in 5G mmWave Vehicular Networks

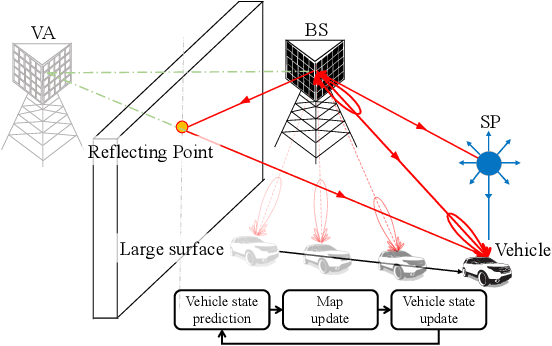
Radio-based vehicular simultaneous localization and mapping (SLAM) aims to localize vehicles while mapping the landmarks in the environment. We propose a sequence of three Poisson multi-Bernoulli mixture (PMBM) based SLAM filters, which handle the entire SLAM problem in a theoretically optimal manner. The complexity of the three proposed SLAM filters is progressively reduced while sustaining high accuracy by deriving SLAM density approximation with the marginalization of nuisance parameters (either vehicle state or data association). Firstly, the PMBM SLAM filter serves as the foundation, for which we provide the first complete description based on a Rao-Blackwellized particle filter. Secondly, the Poisson multi-Bernoulli (PMB) SLAM filter is based on the standard reduction from PMBM to PMB, but involves a novel interpretation based on auxiliary variables and a relation to Bethe free energy. Finally, using the same auxiliary variable argument, we derive a marginalized PMB SLAM filter, which avoids particles and is instead implemented with a low-complexity cubature Kalman filter. We evaluate the three proposed SLAM filters in comparison with the probability hypothesis density (PHD) SLAM filter in 5G mmWave vehicular networks and show the computation-performance trade-off between them.