Post Hoc Extraction of Pareto Fronts for Continuous Control

Agents in the real world must often balance multiple objectives, such as speed, stability, and energy efficiency in continuous control. To account for changing conditions and preferences, an agent must ideally learn a Pareto frontier of policies representing multiple optimal trade-offs. Recent advances in multi-policy multi-objective reinforcement learning (MORL) enable learning a Pareto front directly, but require full multi-objective consideration from the start of training. In practice, multi-objective preferences often arise after a policy has already been trained on a single specialised objective. Existing MORL methods cannot leverage these pre-trained `specialists' to learn Pareto fronts and avoid incurring the sample costs of retraining. We introduce Mixed Advantage Pareto Extraction (MAPEX), an offline MORL method that constructs a frontier of policies by reusing pre-trained specialist policies, critics, and replay buffers. MAPEX combines evaluations from specialist critics into a mixed advantage signal, and weights a behaviour cloning loss with it to train new policies that balance multiple objectives. MAPEX's post hoc Pareto front extraction preserves the simplicity of single-objective off-policy RL, and avoids retrofitting these algorithms into complex MORL frameworks. We formally describe the MAPEX procedure and evaluate MAPEX on five multi-objective MuJoCo environments. Given the same starting policies, MAPEX produces comparable fronts at $0.001\%$ the sample cost of established baselines.

Counterfactual Conditional Likelihood Rewards for Multiagent Exploration

Efficient exploration is critical for multiagent systems to discover coordinated strategies, particularly in open-ended domains such as search and rescue or planetary surveying. However, when exploration is encouraged only at the individual agent level, it often leads to redundancy, as agents act without awareness of how their teammates are exploring. In this work, we introduce Counterfactual Conditional Likelihood (CCL) rewards, which score each agent's exploration by isolating its unique contribution to team exploration. Unlike prior methods that reward agents solely for the novelty of their individual observations, CCL emphasizes observations that are informative with respect to the joint exploration of the team. Experiments in continuous multiagent domains show that CCL rewards accelerate learning for domains with sparse team rewards, where most joint actions yield zero rewards, and are particularly effective in tasks that require tight coordination among agents.

Safe Multiagent Coordination via Entropic Exploration

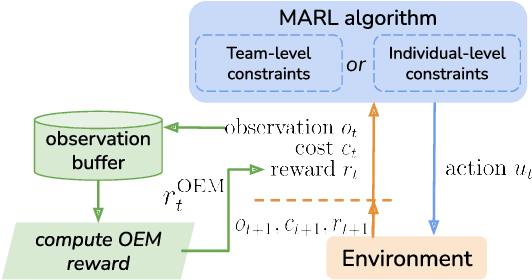
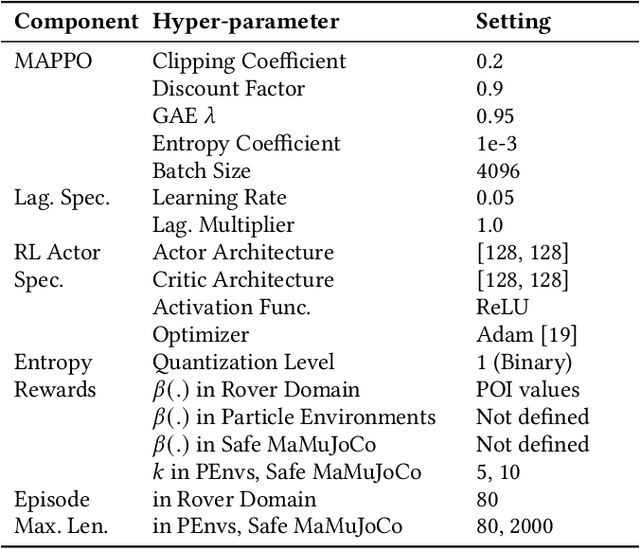
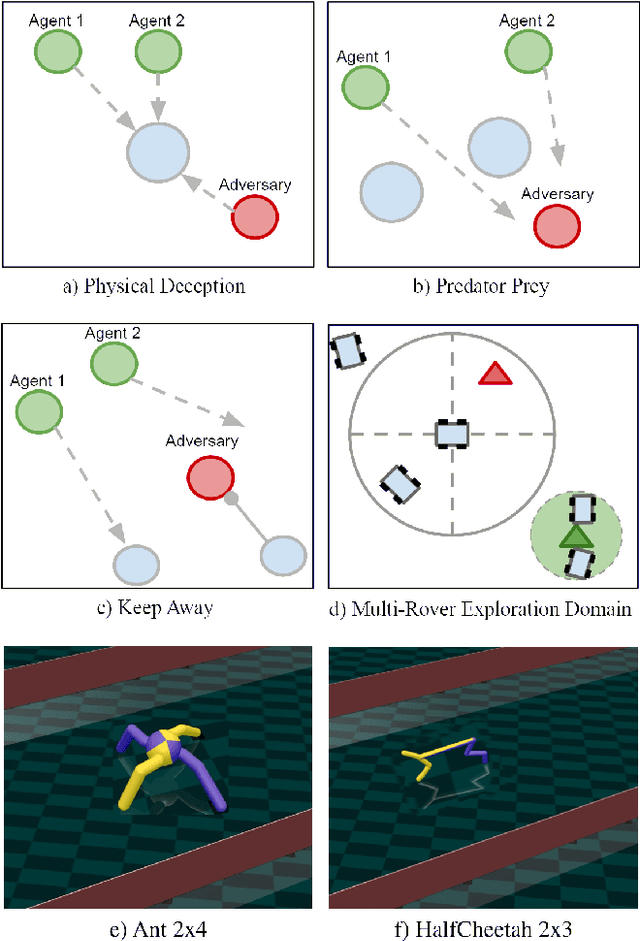
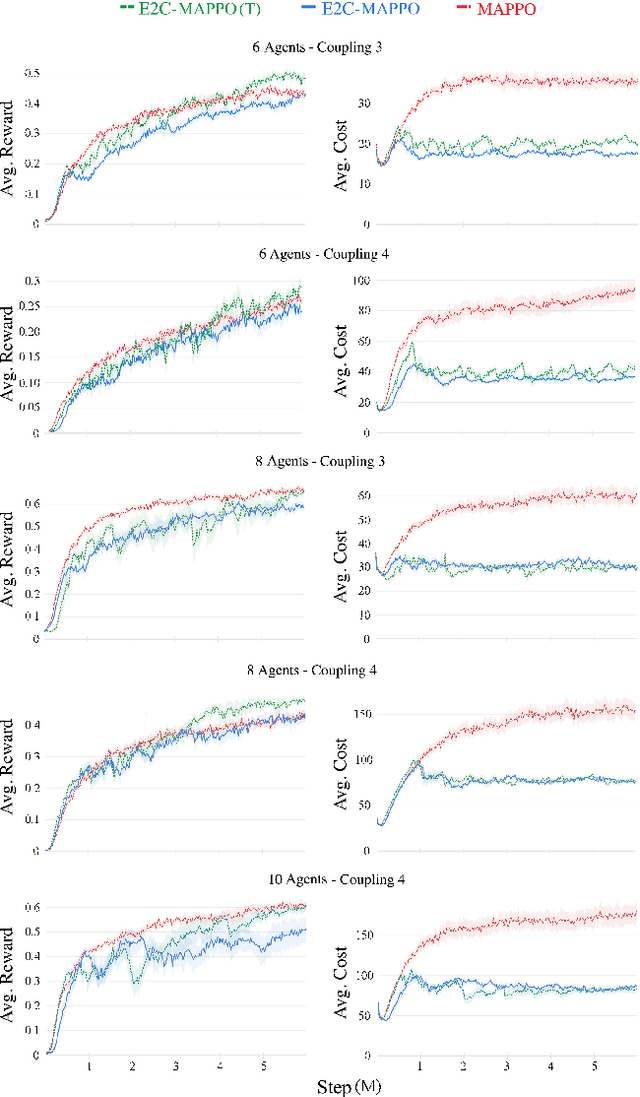
Many real-world multiagent learning problems involve safety concerns. In these setups, typical safe reinforcement learning algorithms constrain agents' behavior, limiting exploration -- a crucial component for discovering effective cooperative multiagent behaviors. Moreover, the multiagent literature typically models individual constraints for each agent and has yet to investigate the benefits of using joint team constraints. In this work, we analyze these team constraints from a theoretical and practical perspective and propose entropic exploration for constrained multiagent reinforcement learning (E2C) to address the exploration issue. E2C leverages observation entropy maximization to incentivize exploration and facilitate learning safe and effective cooperative behaviors. Experiments across increasingly complex domains show that E2C agents match or surpass common unconstrained and constrained baselines in task performance while reducing unsafe behaviors by up to $50\%$.

Evolutionary Reinforcement Learning for Sample-Efficient Multiagent Coordination

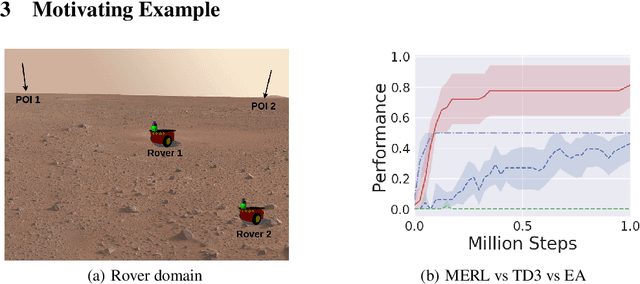
A key challenge for Multiagent RL (Reinforcement Learning) is the design of agent-specific, local rewards that are aligned with sparse global objectives. In this paper, we introduce MERL (Multiagent Evolutionary RL), a hybrid algorithm that does not require an explicit alignment between local and global objectives. MERL uses fast, policy-gradient based learning for each agent by utilizing their dense local rewards. Concurrently, an evolutionary algorithm is used to recruit agents into a team by directly optimizing the sparser global objective. We explore problems that require coupling (a minimum number of agents required to coordinate for success), where the degree of coupling is not known to the agents. We demonstrate that MERL's integrated approach is more sample-efficient and retains performance better with increasing coupling orders compared to MADDPG, the state-of-the-art policy-gradient algorithm for multiagent coordination.

Collaborative Evolutionary Reinforcement Learning

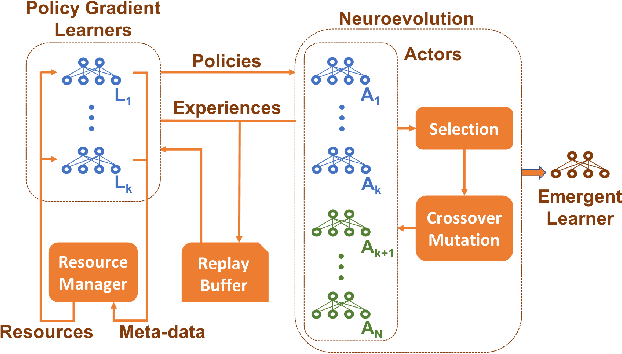
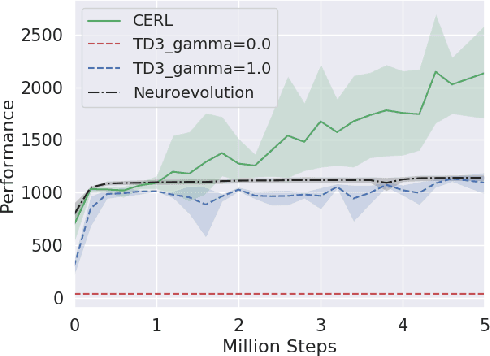
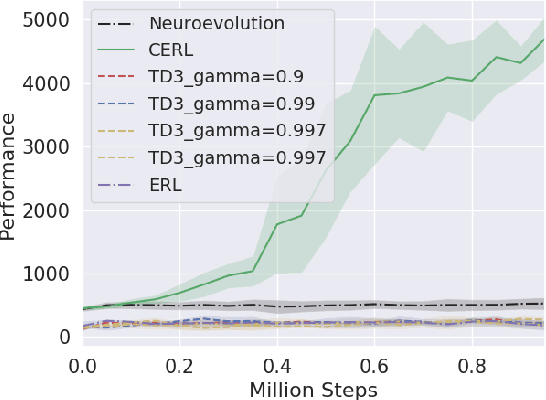
Deep reinforcement learning algorithms have been successfully applied to a range of challenging control tasks. However, these methods typically struggle with achieving effective exploration and are extremely sensitive to the choice of hyperparameters. One reason is that most approaches use a noisy version of their operating policy to explore - thereby limiting the range of exploration. In this paper, we introduce Collaborative Evolutionary Reinforcement Learning (CERL), a scalable framework that comprises a portfolio of policies that simultaneously explore and exploit diverse regions of the solution space. A collection of learners - typically proven algorithms like TD3 - optimize over varying time-horizons leading to this diverse portfolio. All learners contribute to and use a shared replay buffer to achieve greater sample efficiency. Computational resources are dynamically distributed to favor the best learners as a form of online algorithm selection. Neuroevolution binds this entire process to generate a single emergent learner that exceeds the capabilities of any individual learner. Experiments in a range of continuous control benchmarks demonstrate that the emergent learner significantly outperforms its composite learners while remaining overall more sample-efficient - notably solving the Mujoco Humanoid benchmark where all of its composite learners (TD3) fail entirely in isolation.

Evolution-Guided Policy Gradient in Reinforcement Learning

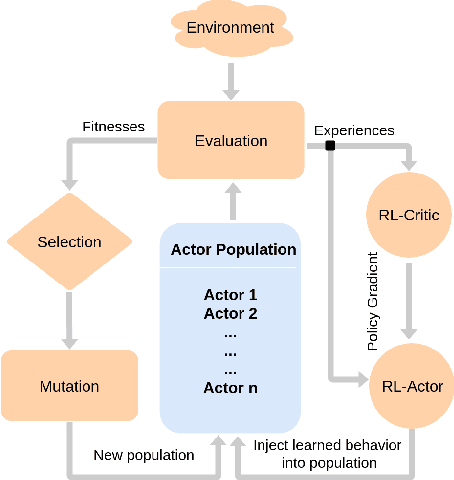
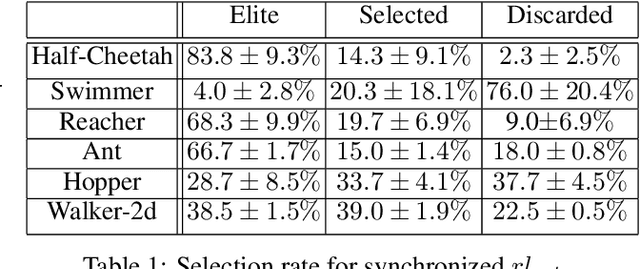
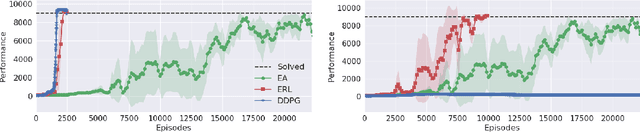
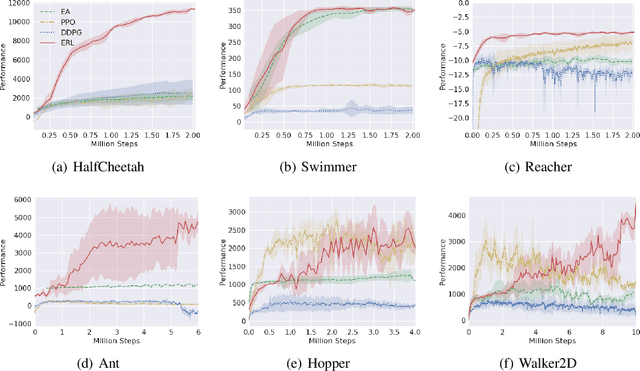
Deep Reinforcement Learning (DRL) algorithms have been successfully applied to a range of challenging control tasks. However, these methods typically suffer from three core difficulties: temporal credit assignment with sparse rewards, lack of effective exploration, and brittle convergence properties that are extremely sensitive to hyperparameters. Collectively, these challenges severely limit the applicability of these approaches to real-world problems. Evolutionary Algorithms (EAs), a class of black box optimization techniques inspired by natural evolution, are well suited to address each of these three challenges. However, EAs typically suffer from high sample complexity and struggle to solve problems that require optimization of a large number of parameters. In this paper, we introduce Evolutionary Reinforcement Learning (ERL), a hybrid algorithm that leverages the population of an EA to provide diversified data to train an RL agent, and reinserts the RL agent into the EA population periodically to inject gradient information into the EA. ERL inherits EA's ability of temporal credit assignment with a fitness metric, effective exploration with a diverse set of policies, and stability of a population-based approach and complements it with off-policy DRL's ability to leverage gradients for higher sample efficiency and faster learning. Experiments in a range of challenging continuous control benchmarks demonstrate that ERL significantly outperforms prior DRL and EA methods.

An Introduction to Collective Intelligence

This paper surveys the emerging science of how to design a ``COllective INtelligence'' (COIN). A COIN is a large multi-agent system where: (i) There is little to no centralized communication or control; and (ii) There is a provided world utility function that rates the possible histories of the full system. In particular, we are interested in COINs in which each agent runs a reinforcement learning (RL) algorithm. Rather than use a conventional modeling approach (e.g., model the system dynamics, and hand-tune agents to cooperate), we aim to solve the COIN design problem implicitly, via the ``adaptive'' character of the RL algorithms of each of the agents. This approach introduces an entirely new, profound design problem: Assuming the RL algorithms are able to achieve high rewards, what reward functions for the individual agents will, when pursued by those agents, result in high world utility? In other words, what reward functions will best ensure that we do not have phenomena like the tragedy of the commons, Braess's paradox, or the liquidity trap? Although still very young, research specifically concentrating on the COIN design problem has already resulted in successes in artificial domains, in particular in packet-routing, the leader-follower problem, and in variants of Arthur's El Farol bar problem. It is expected that as it matures and draws upon other disciplines related to COINs, this research will greatly expand the range of tasks addressable by human engineers. Moreover, in addition to drawing on them, such a fully developed scie nce of COIN design may provide much insight into other already established scientific fields, such as economics, game theory, and population biology.

Collective Intelligence for Control of Distributed Dynamical Systems

We consider the El Farol bar problem, also known as the minority game (W. B. Arthur, ``The American Economic Review'', 84(2): 406--411 (1994), D. Challet and Y.C. Zhang, ``Physica A'', 256:514 (1998)). We view it as an instance of the general problem of how to configure the nodal elements of a distributed dynamical system so that they do not ``work at cross purposes'', in that their collective dynamics avoids frustration and thereby achieves a provided global goal. We summarize a mathematical theory for such configuration applicable when (as in the bar problem) the global goal can be expressed as minimizing a global energy function and the nodes can be expressed as minimizers of local free energy functions. We show that a system designed with that theory performs nearly optimally for the bar problem.

Robust Combining of Disparate Classifiers through Order Statistics

Integrating the outputs of multiple classifiers via combiners or meta-learners has led to substantial improvements in several difficult pattern recognition problems. In the typical setting investigated till now, each classifier is trained on data taken or resampled from a common data set, or (almost) randomly selected subsets thereof, and thus experiences similar quality of training data. However, in certain situations where data is acquired and analyzed on-line at several geographically distributed locations, the quality of data may vary substantially, leading to large discrepancies in performance of individual classifiers. In this article we introduce and investigate a family of classifiers based on order statistics, for robust handling of such cases. Based on a mathematical modeling of how the decision boundaries are affected by order statistic combiners, we derive expressions for the reductions in error expected when such combiners are used. We show analytically that the selection of the median, the maximum and in general, the $i^{th}$ order statistic improves classification performance. Furthermore, we introduce the trim and spread combiners, both based on linear combinations of the ordered classifier outputs, and show that they are quite beneficial in presence of outliers or uneven classifier performance. Experimental results on several public domain data sets corroborate these findings.

Linear and Order Statistics Combiners for Pattern Classification

Several researchers have experimentally shown that substantial improvements can be obtained in difficult pattern recognition problems by combining or integrating the outputs of multiple classifiers. This chapter provides an analytical framework to quantify the improvements in classification results due to combining. The results apply to both linear combiners and order statistics combiners. We first show that to a first order approximation, the error rate obtained over and above the Bayes error rate, is directly proportional to the variance of the actual decision boundaries around the Bayes optimum boundary. Combining classifiers in output space reduces this variance, and hence reduces the "added" error. If N unbiased classifiers are combined by simple averaging, the added error rate can be reduced by a factor of N if the individual errors in approximating the decision boundaries are uncorrelated. Expressions are then derived for linear combiners which are biased or correlated, and the effect of output correlations on ensemble performance is quantified. For order statistics based non-linear combiners, we derive expressions that indicate how much the median, the maximum and in general the ith order statistic can improve classifier performance. The analysis presented here facilitates the understanding of the relationships among error rates, classifier boundary distributions, and combining in output space. Experimental results on several public domain data sets are provided to illustrate the benefits of combining and to support the analytical results.