DOTA: Distributional Test-Time Adaptation of Vision-Language Models

Vision-language foundation models (e.g., CLIP) have shown remarkable performance across a wide range of tasks. However, deploying these models may be unreliable when significant distribution gaps exist between the training and test data. The training-free test-time dynamic adapter (TDA) is a promising approach to address this issue by storing representative test samples to guide the classification of subsequent ones. However, TDA only naively maintains a limited number of reference samples in the cache, leading to severe test-time catastrophic forgetting when the cache is updated by dropping samples. In this paper, we propose a simple yet effective method for DistributiOnal Test-time Adaptation (Dota). Instead of naively memorizing representative test samples, Dota continually estimates the distributions of test samples, allowing the model to continually adapt to the deployment environment. The test-time posterior probabilities are then computed using the estimated distributions based on Bayes' theorem for adaptation purposes. To further enhance the adaptability on the uncertain samples, we introduce a new human-in-the-loop paradigm which identifies uncertain samples, collects human-feedback, and incorporates it into the Dota framework. Extensive experiments validate that Dota enables CLIP to continually learn, resulting in a significant improvement compared to current state-of-the-art methods.

Online Optimization for Learning to Communicate over Time-Correlated Channels

Machine learning techniques have garnered great interest in designing communication systems owing to their capacity in tacking with channel uncertainty. To provide theoretical guarantees for learning-based communication systems, some recent works analyze generalization bounds for devised methods based on the assumption of Independently and Identically Distributed (I.I.D.) channels, a condition rarely met in practical scenarios. In this paper, we drop the I.I.D. channel assumption and study an online optimization problem of learning to communicate over time-correlated channels. To address this issue, we further focus on two specific tasks: optimizing channel decoders for time-correlated fading channels and selecting optimal codebooks for time-correlated additive noise channels. For utilizing temporal dependence of considered channels to better learn communication systems, we develop two online optimization algorithms based on the optimistic online mirror descent framework. Furthermore, we provide theoretical guarantees for proposed algorithms via deriving sub-linear regret bound on the expected error probability of learned systems. Extensive simulation experiments have been conducted to validate that our presented approaches can leverage the channel correlation to achieve a lower average symbol error rate compared to baseline methods, consistent with our theoretical findings.

Learnability in Online Kernel Selection with Memory Constraint via Data-dependent Regret Analysis

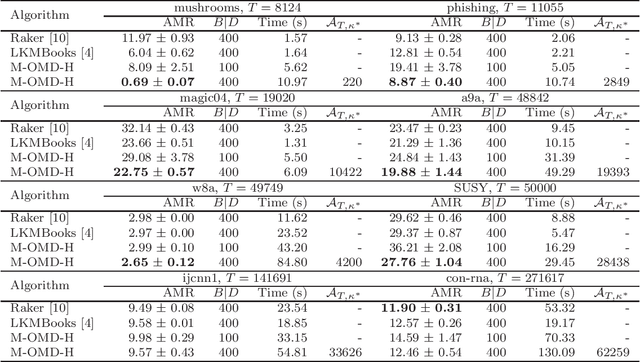
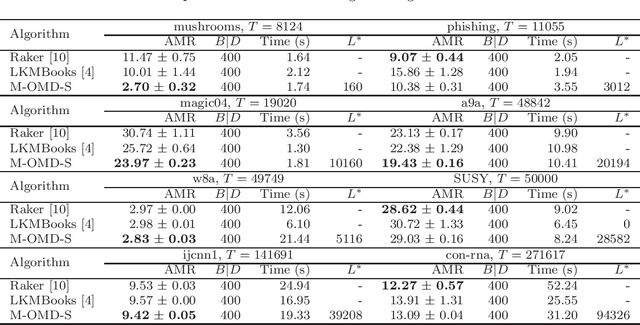
Online kernel selection is a fundamental problem of online kernel methods. In this paper, we study online kernel selection with memory constraint in which the memory of kernel selection and online prediction procedures is limited to a fixed budget. An essential question is what is the intrinsic relationship among online learnability, memory constraint and data complexity? To answer the question, it is necessary to show the trade-offs between regret bound and memory constraint. Previous work gives a worst-case lower bound depending on the data size,and shows learning is impossible within a small memory constraint. In contrast, we present a different result by providing data-dependent upper bounds depending on two data complexities, namely kernel alignment and the cumulative losses of competitive hypothesis. We propose an algorithmic framework giving data-dependent upper bounds for two types of loss functions. For the hinge loss function, our algorithm achieves an expected upper bound depending on kernel alignment. For smooth loss functions,our algorithm achieves a high-probability upper bound depending on the cumulative losses of competitive hypothesis. We also prove a matching lower bound for smooth loss functions. Our results show that if the two data complexities are sub-linear, then learning is possible within a small memory constraint. Our algorithmic framework depends on a new buffer maintaining framework and a reduction from online kernel selection to prediction with expert advice.Finally, we empirically verify the prediction performance of our algorithms on benchmark datasets.

On the Necessity of Collaboration in Online Model Selection with Decentralized Data

We consider online model selection with decentralized data over $M$ clients, and study a fundamental problem: the necessity of collaboration. Previous work gave a negative answer from the perspective of worst-case regret minimization, while we give a different answer from the perspective of regret-computational cost trade-off. We separately propose a federated algorithm with and without communication constraint and prove regret bounds that show (i) collaboration is unnecessary if we do not limit the computational cost on each client; (ii) collaboration is necessary if we limit the computational cost on each client to $o(K)$, where $K$ is the number of candidate hypothesis spaces. As a by-product, we improve the regret bounds of algorithms for distributed online multi-kernel learning at a smaller computational and communication cost. Our algorithms rely on three new techniques, i.e., an improved Bernstein's inequality for martingale, a federated algorithmic framework, named FOMD-No-LU, and decoupling model selection and predictions, which might be of independent interest.

Topology Learning for Heterogeneous Decentralized Federated Learning over Unreliable D2D Networks

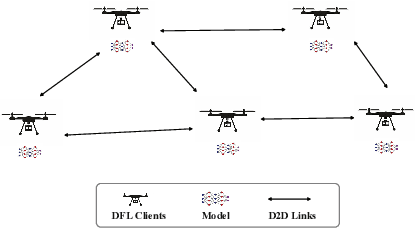
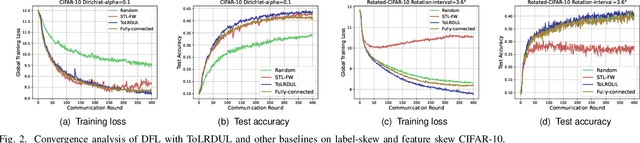
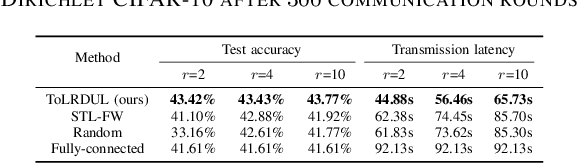
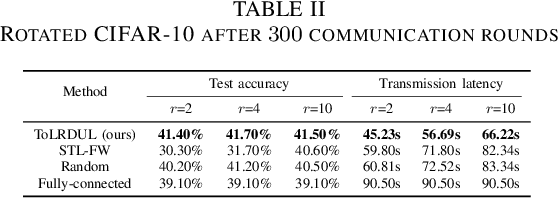
With the proliferation of intelligent mobile devices in wireless device-to-device (D2D) networks, decentralized federated learning (DFL) has attracted significant interest. Compared to centralized federated learning (CFL), DFL mitigates the risk of central server failures due to communication bottlenecks. However, DFL faces several challenges, such as the severe heterogeneity of data distributions in diverse environments, and the transmission outages and package errors caused by the adoption of the User Datagram Protocol (UDP) in D2D networks. These challenges often degrade the convergence of training DFL models. To address these challenges, we conduct a thorough theoretical convergence analysis for DFL and derive a convergence bound. By defining a novel quantity named unreliable links-aware neighborhood discrepancy in this convergence bound, we formulate a tractable optimization objective, and develop a novel Topology Learning method considering the Representation Discrepancy and Unreliable Links in DFL, named ToLRDUL. Intensive experiments under both feature skew and label skew settings have validated the effectiveness of our proposed method, demonstrating improved convergence speed and test accuracy, consistent with our theoretical findings.

Ahpatron: A New Budgeted Online Kernel Learning Machine with Tighter Mistake Bound

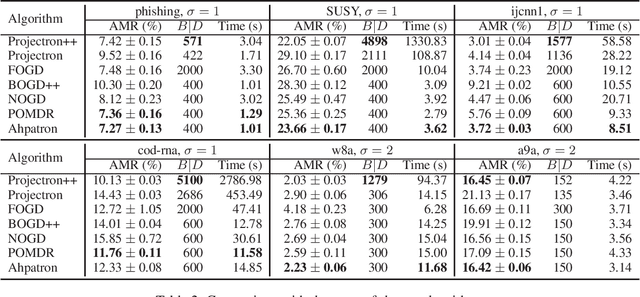
In this paper, we study the mistake bound of online kernel learning on a budget. We propose a new budgeted online kernel learning model, called Ahpatron, which significantly improves the mistake bound of previous work and resolves the open problem posed by Dekel, Shalev-Shwartz, and Singer (2005). We first present an aggressive variant of Perceptron, named AVP, a model without budget, which uses an active updating rule. Then we design a new budget maintenance mechanism, which removes a half of examples,and projects the removed examples onto a hypothesis space spanned by the remaining examples. Ahpatron adopts the above mechanism to approximate AVP. Theoretical analyses prove that Ahpatron has tighter mistake bounds, and experimental results show that Ahpatron outperforms the state-of-the-art algorithms on the same or a smaller budget.

Nearly Optimal Algorithms with Sublinear Computational Complexity for Online Kernel Regression

The trade-off between regret and computational cost is a fundamental problem for online kernel regression, and previous algorithms worked on the trade-off can not keep optimal regret bounds at a sublinear computational complexity. In this paper, we propose two new algorithms, AOGD-ALD and NONS-ALD, which can keep nearly optimal regret bounds at a sublinear computational complexity, and give sufficient conditions under which our algorithms work. Both algorithms dynamically maintain a group of nearly orthogonal basis used to approximate the kernel mapping, and keep nearly optimal regret bounds by controlling the approximate error. The number of basis depends on the approximate error and the decay rate of eigenvalues of the kernel matrix. If the eigenvalues decay exponentially, then AOGD-ALD and NONS-ALD separately achieves a regret of $O(\sqrt{L(f)})$ and $O(\mathrm{d}_{\mathrm{eff}}(\mu)\ln{T})$ at a computational complexity in $O(\ln^2{T})$. If the eigenvalues decay polynomially with degree $p\geq 1$, then our algorithms keep the same regret bounds at a computational complexity in $o(T)$ in the case of $p>4$ and $p\geq 10$, respectively. $L(f)$ is the cumulative losses of $f$ and $\mathrm{d}_{\mathrm{eff}}(\mu)$ is the effective dimension of the problem. The two regret bounds are nearly optimal and are not comparable.

Improved Regret Bounds for Online Kernel Selection under Bandit Feedback

In this paper, we improve the regret bound for online kernel selection under bandit feedback. Previous algorithm enjoys a $O((\Vert f\Vert^2_{\mathcal{H}_i}+1)K^{\frac{1}{3}}T^{\frac{2}{3}})$ expected bound for Lipschitz loss functions. We prove two types of regret bounds improving the previous bound. For smooth loss functions, we propose an algorithm with a $O(U^{\frac{2}{3}}K^{-\frac{1}{3}}(\sum^K_{i=1}L_T(f^\ast_i))^{\frac{2}{3}})$ expected bound where $L_T(f^\ast_i)$ is the cumulative losses of optimal hypothesis in $\mathbb{H}_{i}=\{f\in\mathcal{H}_i:\Vert f\Vert_{\mathcal{H}_i}\leq U\}$. The data-dependent bound keeps the previous worst-case bound and is smaller if most of candidate kernels match well with the data. For Lipschitz loss functions, we propose an algorithm with a $O(U\sqrt{KT}\ln^{\frac{2}{3}}{T})$ expected bound asymptotically improving the previous bound. We apply the two algorithms to online kernel selection with time constraint and prove new regret bounds matching or improving the previous $O(\sqrt{T\ln{K}} +\Vert f\Vert^2_{\mathcal{H}_i}\max\{\sqrt{T},\frac{T}{\sqrt{\mathcal{R}}}\})$ expected bound where $\mathcal{R}$ is the time budget. Finally, we empirically verify our algorithms on online regression and classification tasks.

Improved Kernel Alignment Regret Bound for Online Kernel Learning

In this paper, we improve the kernel alignment regret bound for online kernel learning in the regime of the Hinge loss function. Previous algorithm achieves a regret of $O((\mathcal{A}_TT\ln{T})^{\frac{1}{4}})$ at a computational complexity (space and per-round time) of $O(\sqrt{\mathcal{A}_TT\ln{T}})$, where $\mathcal{A}_T$ is called \textit{kernel alignment}. We propose an algorithm whose regret bound and computational complexity are better than previous results. Our results depend on the decay rate of eigenvalues of the kernel matrix. If the eigenvalues of the kernel matrix decay exponentially, then our algorithm enjoys a regret of $O(\sqrt{\mathcal{A}_T})$ at a computational complexity of $O(\ln^2{T})$. Otherwise, our algorithm enjoys a regret of $O((\mathcal{A}_TT)^{\frac{1}{4}})$ at a computational complexity of $O(\sqrt{\mathcal{A}_TT})$. We extend our algorithm to batch learning and obtain a $O(\frac{1}{T}\sqrt{\mathbb{E}[\mathcal{A}_T]})$ excess risk bound which improves the previous $O(1/\sqrt{T})$ bound.