Learnability in Online Kernel Selection with Memory Constraint via Data-dependent Regret Analysis

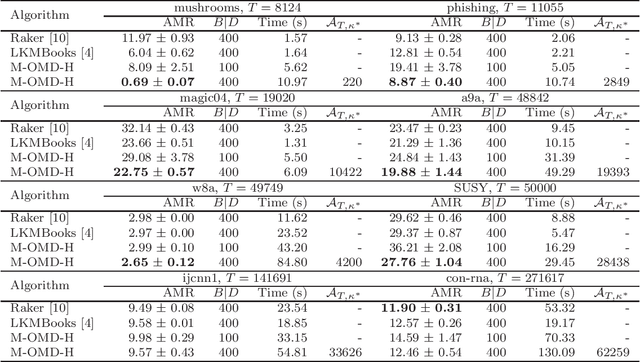
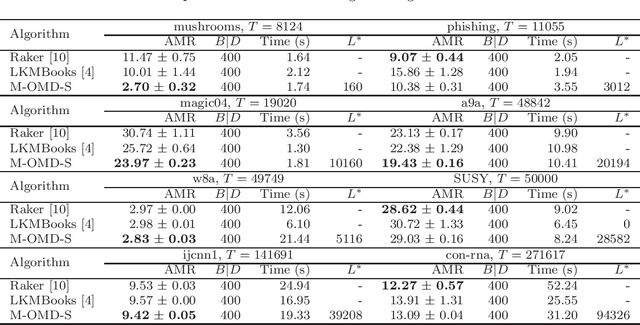
Online kernel selection is a fundamental problem of online kernel methods. In this paper, we study online kernel selection with memory constraint in which the memory of kernel selection and online prediction procedures is limited to a fixed budget. An essential question is what is the intrinsic relationship among online learnability, memory constraint and data complexity? To answer the question, it is necessary to show the trade-offs between regret bound and memory constraint. Previous work gives a worst-case lower bound depending on the data size,and shows learning is impossible within a small memory constraint. In contrast, we present a different result by providing data-dependent upper bounds depending on two data complexities, namely kernel alignment and the cumulative losses of competitive hypothesis. We propose an algorithmic framework giving data-dependent upper bounds for two types of loss functions. For the hinge loss function, our algorithm achieves an expected upper bound depending on kernel alignment. For smooth loss functions,our algorithm achieves a high-probability upper bound depending on the cumulative losses of competitive hypothesis. We also prove a matching lower bound for smooth loss functions. Our results show that if the two data complexities are sub-linear, then learning is possible within a small memory constraint. Our algorithmic framework depends on a new buffer maintaining framework and a reduction from online kernel selection to prediction with expert advice.Finally, we empirically verify the prediction performance of our algorithms on benchmark datasets.