Physical Information Neural Networks for Solving High-index Differential-algebraic Equation Systems Based on Radau Methods

As is well known, differential algebraic equations (DAEs), which are able to describe dynamic changes and underlying constraints, have been widely applied in engineering fields such as fluid dynamics, multi-body dynamics, mechanical systems and control theory. In practical physical modeling within these domains, the systems often generate high-index DAEs. Classical implicit numerical methods typically result in varying order reduction of numerical accuracy when solving high-index systems.~Recently, the physics-informed neural network (PINN) has gained attention for solving DAE systems. However, it faces challenges like the inability to directly solve high-index systems, lower predictive accuracy, and weaker generalization capabilities. In this paper, we propose a PINN computational framework, combined Radau IIA numerical method with a neural network structure via the attention mechanisms, to directly solve high-index DAEs. Furthermore, we employ a domain decomposition strategy to enhance solution accuracy. We conduct numerical experiments with two classical high-index systems as illustrative examples, investigating how different orders of the Radau IIA method affect the accuracy of neural network solutions. The experimental results demonstrate that the PINN based on a 5th-order Radau IIA method achieves the highest level of system accuracy. Specifically, the absolute errors for all differential variables remains as low as $10^{-6}$, and the absolute errors for algebraic variables is maintained at $10^{-5}$, surpassing the results found in existing literature. Therefore, our method exhibits excellent computational accuracy and strong generalization capabilities, providing a feasible approach for the high-precision solution of larger-scale DAEs with higher indices or challenging high-dimensional partial differential algebraic equation systems.

Deep learning radiomics for assessment of gastroesophageal varices in people with compensated advanced chronic liver disease

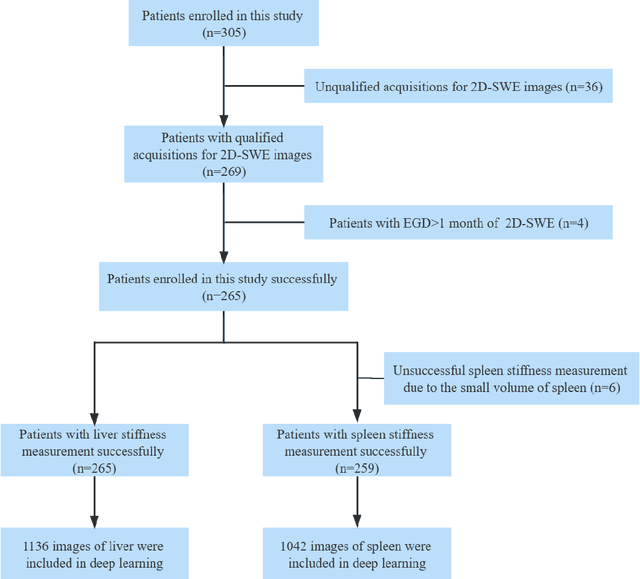
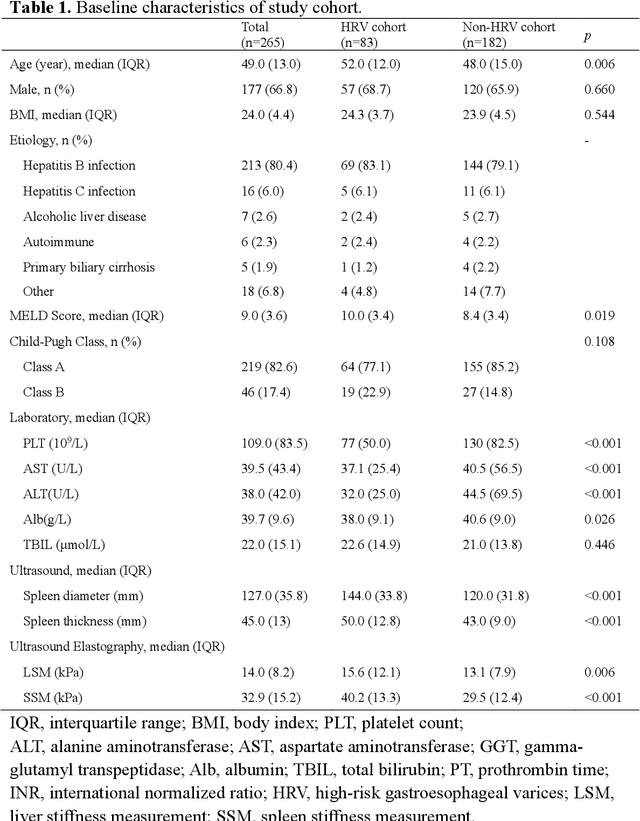
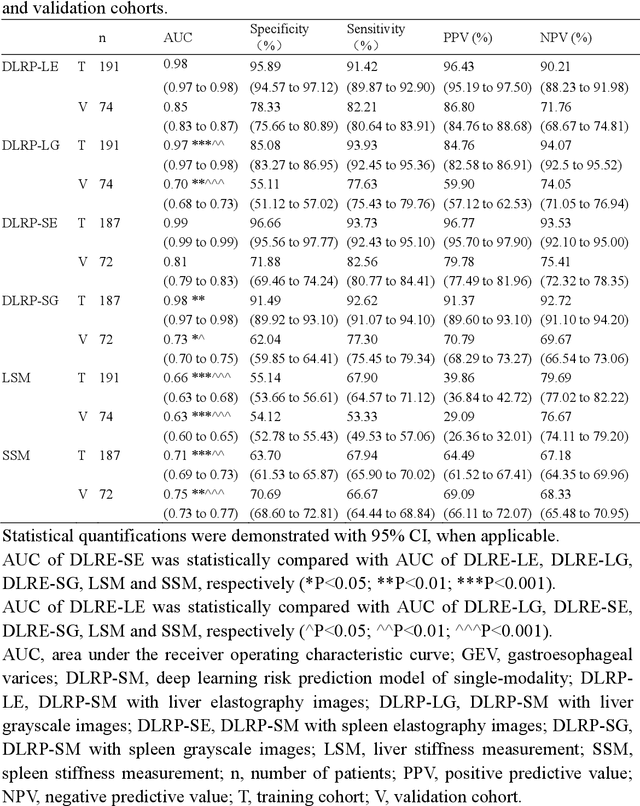
Objective: Bleeding from gastroesophageal varices (GEV) is a medical emergency associated with high mortality. We aim to construct an artificial intelligence-based model of two-dimensional shear wave elastography (2D-SWE) of the liver and spleen to precisely assess the risk of GEV and high-risk gastroesophageal varices (HRV). Design: A prospective multicenter study was conducted in patients with compensated advanced chronic liver disease. 305 patients were enrolled from 12 hospitals, and finally 265 patients were included, with 1136 liver stiffness measurement (LSM) images and 1042 spleen stiffness measurement (SSM) images generated by 2D-SWE. We leveraged deep learning methods to uncover associations between image features and patient risk, and thus conducted models to predict GEV and HRV. Results: A multi-modality Deep Learning Risk Prediction model (DLRP) was constructed to assess GEV and HRV, based on LSM and SSM images, and clinical information. Validation analysis revealed that the AUCs of DLRP were 0.91 for GEV (95% CI 0.90 to 0.93, p < 0.05) and 0.88 for HRV (95% CI 0.86 to 0.89, p < 0.01), which were significantly and robustly better than canonical risk indicators, including the value of LSM and SSM. Moreover, DLPR was better than the model using individual parameters, including LSM and SSM images. In HRV prediction, the 2D-SWE images of SSM outperform LSM (p < 0.01). Conclusion: DLRP shows excellent performance in predicting GEV and HRV over canonical risk indicators LSM and SSM. Additionally, the 2D-SWE images of SSM provided more information for better accuracy in predicting HRV than the LSM.

Multi-class Label Noise Learning via Loss Decomposition and Centroid Estimation

In real-world scenarios, many large-scale datasets often contain inaccurate labels, i.e., noisy labels, which may confuse model training and lead to performance degradation. To overcome this issue, Label Noise Learning (LNL) has recently attracted much attention, and various methods have been proposed to design an unbiased risk estimator to the noise-free dataset to combat such label noise. Among them, a trend of works based on Loss Decomposition and Centroid Estimation (LDCE) has shown very promising performance. However, existing LNL methods based on LDCE are only designed for binary classification, and they are not directly extendable to multi-class situations. In this paper, we propose a novel multi-class robust learning method for LDCE, which is termed "MC-LDCE". Specifically, we decompose the commonly adopted loss (e.g., mean squared loss) function into a label-dependent part and a label-independent part, in which only the former is influenced by label noise. Further, by defining a new form of data centroid, we transform the recovery problem of a label-dependent part to a centroid estimation problem. Finally, by critically examining the mathematical expectation of clean data centroid given the observed noisy set, the centroid can be estimated which helps to build an unbiased risk estimator for multi-class learning. The proposed MC-LDCE method is general and applicable to different types (i.e., linear and nonlinear) of classification models. The experimental results on five public datasets demonstrate the superiority of the proposed MC-LDCE against other representative LNL methods in tackling multi-class label noise problem.