Physical Information Neural Networks for Solving High-index Differential-algebraic Equation Systems Based on Radau Methods

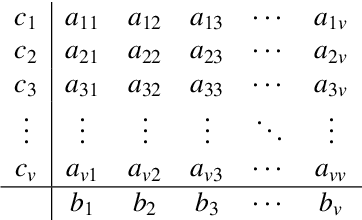
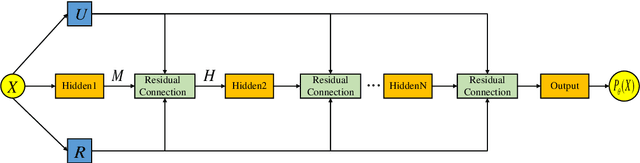
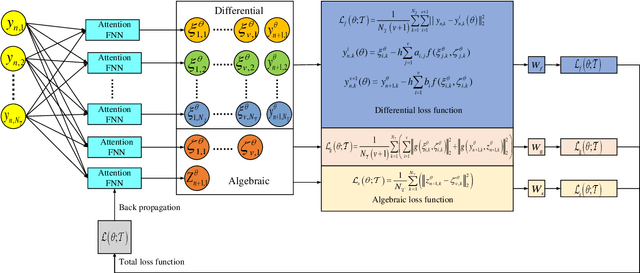
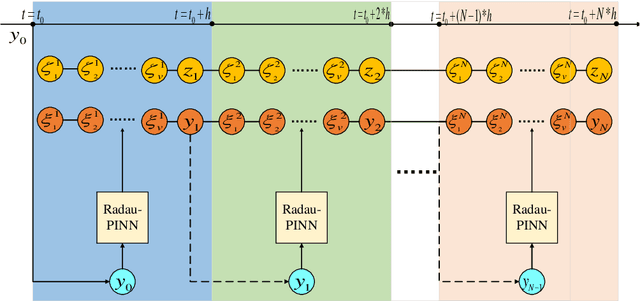
As is well known, differential algebraic equations (DAEs), which are able to describe dynamic changes and underlying constraints, have been widely applied in engineering fields such as fluid dynamics, multi-body dynamics, mechanical systems and control theory. In practical physical modeling within these domains, the systems often generate high-index DAEs. Classical implicit numerical methods typically result in varying order reduction of numerical accuracy when solving high-index systems.~Recently, the physics-informed neural network (PINN) has gained attention for solving DAE systems. However, it faces challenges like the inability to directly solve high-index systems, lower predictive accuracy, and weaker generalization capabilities. In this paper, we propose a PINN computational framework, combined Radau IIA numerical method with a neural network structure via the attention mechanisms, to directly solve high-index DAEs. Furthermore, we employ a domain decomposition strategy to enhance solution accuracy. We conduct numerical experiments with two classical high-index systems as illustrative examples, investigating how different orders of the Radau IIA method affect the accuracy of neural network solutions. The experimental results demonstrate that the PINN based on a 5th-order Radau IIA method achieves the highest level of system accuracy. Specifically, the absolute errors for all differential variables remains as low as $10^{-6}$, and the absolute errors for algebraic variables is maintained at $10^{-5}$, surpassing the results found in existing literature. Therefore, our method exhibits excellent computational accuracy and strong generalization capabilities, providing a feasible approach for the high-precision solution of larger-scale DAEs with higher indices or challenging high-dimensional partial differential algebraic equation systems.

A Multiple Filter Based Neural Network Approach to the Extrapolation of Adsorption Energies on Metal Surfaces for Catalysis Applications

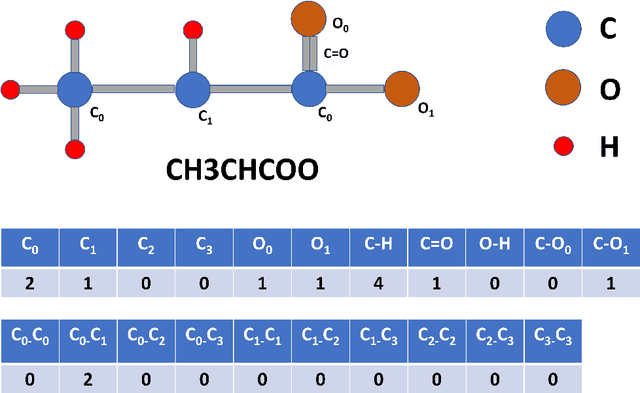
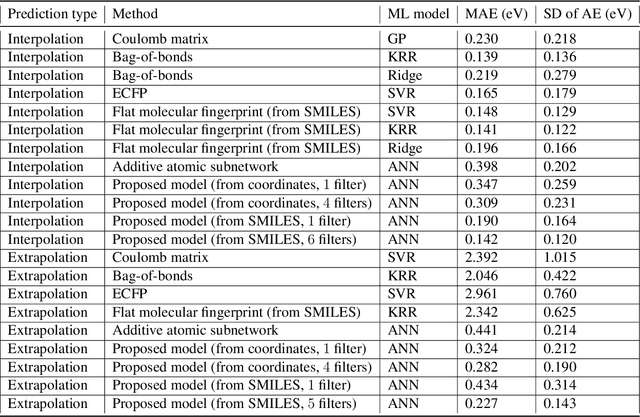
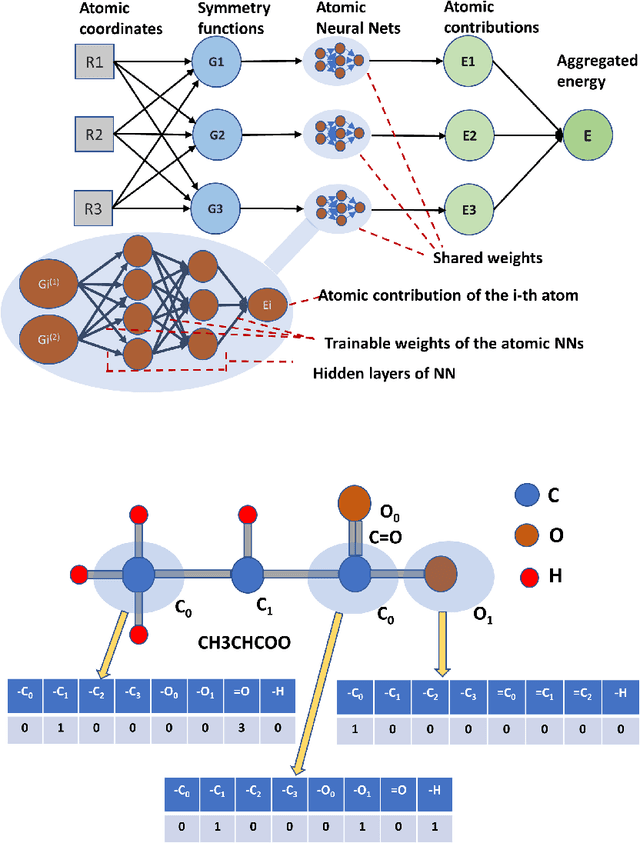
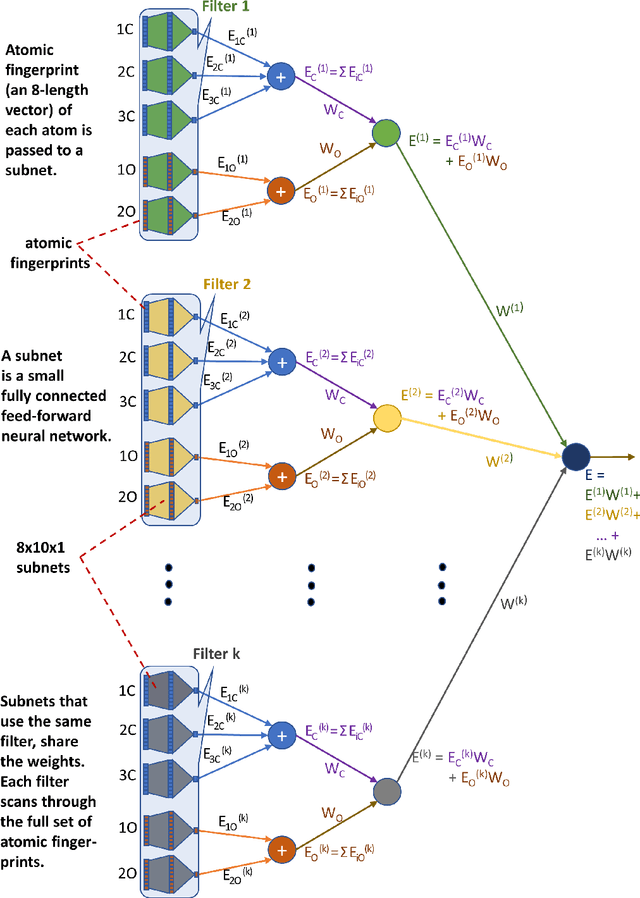
Computational catalyst discovery involves the development of microkinetic reactor models based on estimated parameters determined from density functional theory (DFT). For complex surface chemistries, the cost of calculating the adsorption energies by DFT for a large number of reaction intermediates can become prohibitive. Here, we have identified appropriate descriptors and machine learning models that can be used to predict part of these adsorption energies given data on the rest of them. Our investigations also included the case when the species data used to train the predictive model is of different size relative to the species the model tries to predict - an extrapolation in the data space which is typically difficult with regular machine learning models. We have developed a neural network based predictive model that combines an established model with the concepts of a convolutional neural network that, when extrapolating, achieves significant improvement over the previous models.