Kun Liang
ORBIT: On-policy Exploration-Exploitation for Controllable Multi-Budget Reasoning
Jan 13, 2026Abstract:Recent Large Reasoning Models (LRMs) achieve strong performance by leveraging long-form Chain-of-Thought (CoT) reasoning, but uniformly applying overlong reasoning at inference time incurs substantial and often unnecessary computational cost. To address this, prior work explores various strategies to infer an appropriate reasoning budget from the input. However, such approaches are unreliable in the worst case, as estimating the minimal required reasoning effort is fundamentally difficult, and they implicitly fix the trade-off between reasoning cost and accuracy during training, limiting flexibility under varying deployment scenarios. Motivated by these limitations, we propose ORBIT, a controllable multi-budget reasoning framework with well-separated reasoning modes triggered by input. ORBIT employs multi-stage reinforcement learning to discover Pareto-optimal reasoning behaviors at each effort, followed by on-policy distillation to fuse these behaviors into a single unified model. Experiments show that ORBIT achieves (1) controllable reasoning behavior over multiple modes, (2) competitive reasoning density within each mode, and (3) integration of these frontier policies into a single unified student model while preserving clear mode separation and high per-mode performance.
Composable Cross-prompt Essay Scoring by Merging Models
May 24, 2025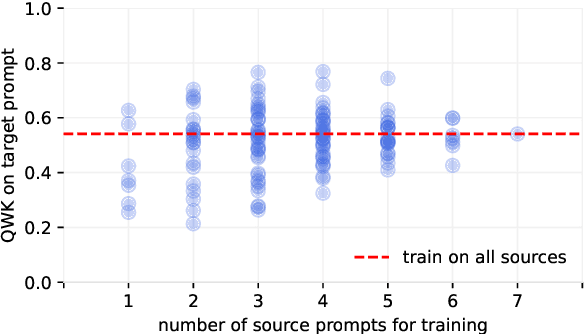

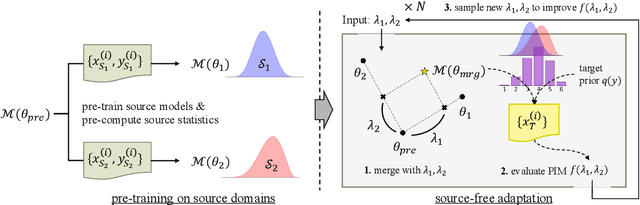
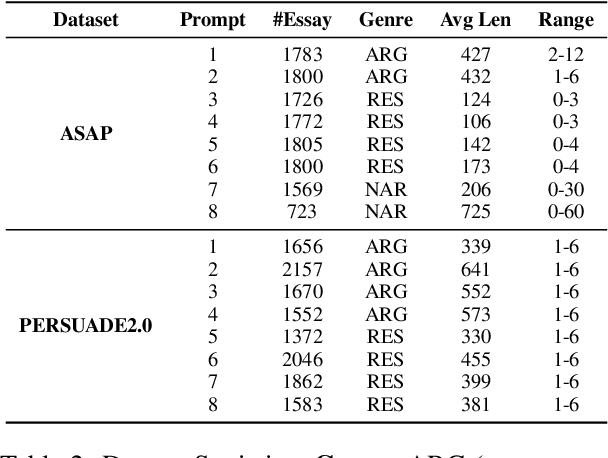
Abstract:Recent advances in cross-prompt automated essay scoring (AES) typically train models jointly on all source prompts, often requiring additional access to unlabeled target prompt essays simultaneously. However, using all sources is suboptimal in our pilot study, and re-accessing source datasets during adaptation raises privacy concerns. We propose a source-free adaptation approach that selectively merges individually trained source models' parameters instead of datasets. In particular, we simulate joint training through linear combinations of task vectors -- the parameter updates from fine-tuning. To optimize the combination's coefficients, we propose Prior-encoded Information Maximization (PIM), an unsupervised objective which promotes the model's score discriminability regularized by priors pre-computed from the sources. We employ Bayesian optimization as an efficient optimizer of PIM. Experimental results with LLMs on in-dataset and cross-dataset adaptation show that our method (1) consistently outperforms training jointly on all sources, (2) maintains superior robustness compared to other merging methods, (3) excels under severe distribution shifts where recent leading cross-prompt methods struggle, all while retaining computational efficiency.
Rank-Then-Score: Enhancing Large Language Models for Automated Essay Scoring
Apr 08, 2025Abstract:In recent years, large language models (LLMs) achieve remarkable success across a variety of tasks. However, their potential in the domain of Automated Essay Scoring (AES) remains largely underexplored. Moreover, compared to English data, the methods for Chinese AES is not well developed. In this paper, we propose Rank-Then-Score (RTS), a fine-tuning framework based on large language models to enhance their essay scoring capabilities. Specifically, we fine-tune the ranking model (Ranker) with feature-enriched data, and then feed the output of the ranking model, in the form of a candidate score set, with the essay content into the scoring model (Scorer) to produce the final score. Experimental results on two benchmark datasets, HSK and ASAP, demonstrate that RTS consistently outperforms the direct prompting (Vanilla) method in terms of average QWK across all LLMs and datasets, and achieves the best performance on Chinese essay scoring using the HSK dataset.
Physical Information Neural Networks for Solving High-index Differential-algebraic Equation Systems Based on Radau Methods
Oct 19, 2023
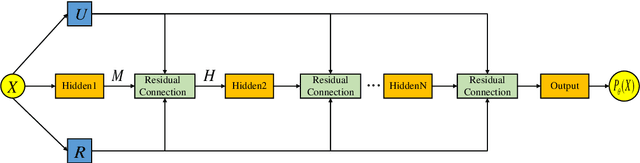
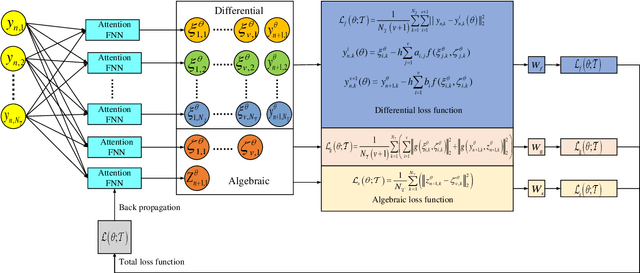
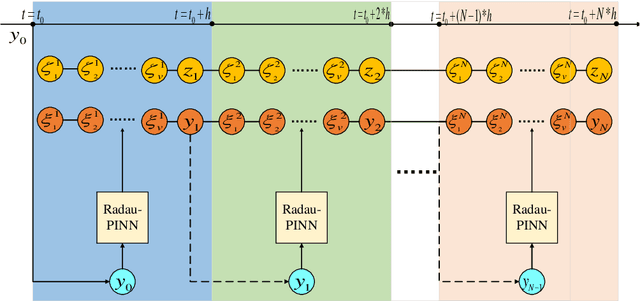
Abstract:As is well known, differential algebraic equations (DAEs), which are able to describe dynamic changes and underlying constraints, have been widely applied in engineering fields such as fluid dynamics, multi-body dynamics, mechanical systems and control theory. In practical physical modeling within these domains, the systems often generate high-index DAEs. Classical implicit numerical methods typically result in varying order reduction of numerical accuracy when solving high-index systems.~Recently, the physics-informed neural network (PINN) has gained attention for solving DAE systems. However, it faces challenges like the inability to directly solve high-index systems, lower predictive accuracy, and weaker generalization capabilities. In this paper, we propose a PINN computational framework, combined Radau IIA numerical method with a neural network structure via the attention mechanisms, to directly solve high-index DAEs. Furthermore, we employ a domain decomposition strategy to enhance solution accuracy. We conduct numerical experiments with two classical high-index systems as illustrative examples, investigating how different orders of the Radau IIA method affect the accuracy of neural network solutions. The experimental results demonstrate that the PINN based on a 5th-order Radau IIA method achieves the highest level of system accuracy. Specifically, the absolute errors for all differential variables remains as low as $10^{-6}$, and the absolute errors for algebraic variables is maintained at $10^{-5}$, surpassing the results found in existing literature. Therefore, our method exhibits excellent computational accuracy and strong generalization capabilities, providing a feasible approach for the high-precision solution of larger-scale DAEs with higher indices or challenging high-dimensional partial differential algebraic equation systems.
Reinforcement Learning Guided Multi-Objective Exam Paper Generation
Mar 02, 2023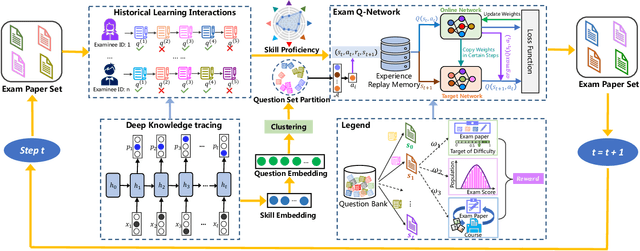

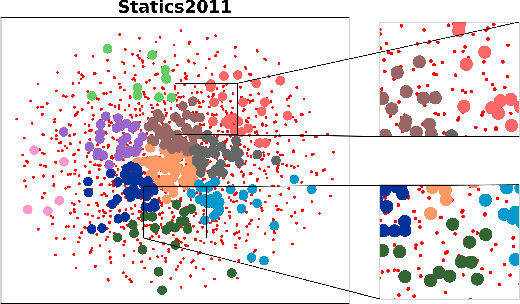
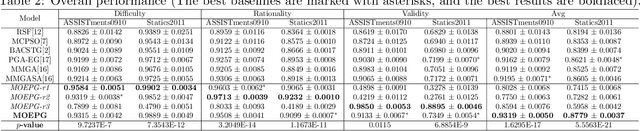
Abstract:To reduce the repetitive and complex work of instructors, exam paper generation (EPG) technique has become a salient topic in the intelligent education field, which targets at generating high-quality exam paper automatically according to instructor-specified assessment criteria. The current advances utilize the ability of heuristic algorithms to optimize several well-known objective constraints, such as difficulty degree, number of questions, etc., for producing optimal solutions. However, in real scenarios, considering other equally relevant objectives (e.g., distribution of exam scores, skill coverage) is extremely important. Besides, how to develop an automatic multi-objective solution that finds an optimal subset of questions from a huge search space of large-sized question datasets and thus composes a high-quality exam paper is urgent but non-trivial. To this end, we skillfully design a reinforcement learning guided Multi-Objective Exam Paper Generation framework, termed MOEPG, to simultaneously optimize three exam domain-specific objectives including difficulty degree, distribution of exam scores, and skill coverage. Specifically, to accurately measure the skill proficiency of the examinee group, we first employ deep knowledge tracing to model the interaction information between examinees and response logs. We then design the flexible Exam Q-Network, a function approximator, which automatically selects the appropriate question to update the exam paper composition process. Later, MOEPG divides the decision space into multiple subspaces to better guide the updated direction of the exam paper. Through extensive experiments on two real-world datasets, we demonstrate that MOEPG is feasible in addressing the multiple dilemmas of exam paper generation scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge