Joseph W. Durham
Multi-robot Path Planning and Scheduling via Model Predictive Optimal Transport (MPC-OT)
Aug 28, 2025Abstract:In this paper, we propose a novel methodology for path planning and scheduling for multi-robot navigation that is based on optimal transport theory and model predictive control. We consider a setup where $N$ robots are tasked to navigate to $M$ targets in a common space with obstacles. Mapping robots to targets first and then planning paths can result in overlapping paths that lead to deadlocks. We derive a strategy based on optimal transport that not only provides minimum cost paths from robots to targets but also guarantees non-overlapping trajectories. We achieve this by discretizing the space of interest into $K$ cells and by imposing a ${K\times K}$ cost structure that describes the cost of transitioning from one cell to another. Optimal transport then provides \textit{optimal and non-overlapping} cell transitions for the robots to reach the targets that can be readily deployed without any scheduling considerations. The proposed solution requires $\unicode{x1D4AA}(K^3\log K)$ computations in the worst-case and $\unicode{x1D4AA}(K^2\log K)$ for well-behaved problems. To further accommodate potentially overlapping trajectories (unavoidable in certain situations) as well as robot dynamics, we show that a temporal structure can be integrated into optimal transport with the help of \textit{replans} and \textit{model predictive control}.
DeepFleet: Multi-Agent Foundation Models for Mobile Robots
Aug 12, 2025
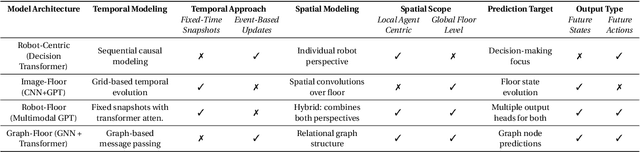
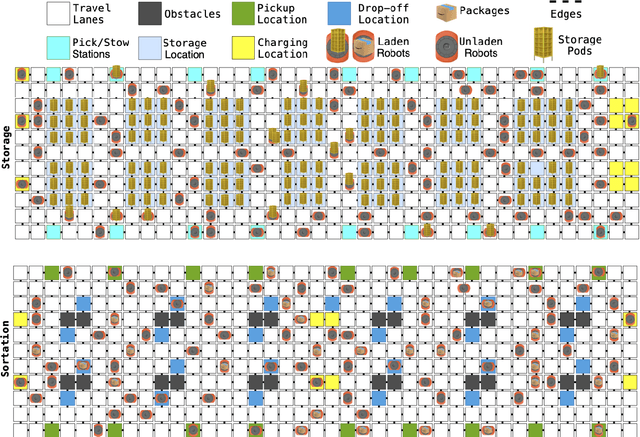
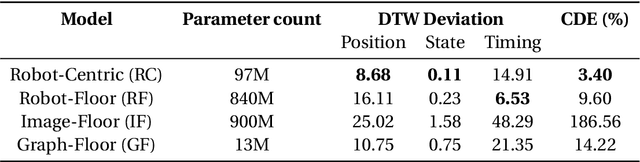
Abstract:We introduce DeepFleet, a suite of foundation models designed to support coordination and planning for large-scale mobile robot fleets. These models are trained on fleet movement data, including robot positions, goals, and interactions, from hundreds of thousands of robots in Amazon warehouses worldwide. DeepFleet consists of four architectures that each embody a distinct inductive bias and collectively explore key points in the design space for multi-agent foundation models: the robot-centric (RC) model is an autoregressive decision transformer operating on neighborhoods of individual robots; the robot-floor (RF) model uses a transformer with cross-attention between robots and the warehouse floor; the image-floor (IF) model applies convolutional encoding to a multi-channel image representation of the full fleet; and the graph-floor (GF) model combines temporal attention with graph neural networks for spatial relationships. In this paper, we describe these models and present our evaluation of the impact of these design choices on prediction task performance. We find that the robot-centric and graph-floor models, which both use asynchronous robot state updates and incorporate the localized structure of robot interactions, show the most promise. We also present experiments that show that these two models can make effective use of larger warehouses operation datasets as the models are scaled up.
Distributionally Robust Multi-Agent Reinforcement Learning for Dynamic Chute Mapping
Mar 12, 2025Abstract:In Amazon robotic warehouses, the destination-to-chute mapping problem is crucial for efficient package sorting. Often, however, this problem is complicated by uncertain and dynamic package induction rates, which can lead to increased package recirculation. To tackle this challenge, we introduce a Distributionally Robust Multi-Agent Reinforcement Learning (DRMARL) framework that learns a destination-to-chute mapping policy that is resilient to adversarial variations in induction rates. Specifically, DRMARL relies on group distributionally robust optimization (DRO) to learn a policy that performs well not only on average but also on each individual subpopulation of induction rates within the group that capture, for example, different seasonality or operation modes of the system. This approach is then combined with a novel contextual bandit-based predictor of the worst-case induction distribution for each state-action pair, significantly reducing the cost of exploration and thereby increasing the learning efficiency and scalability of our framework. Extensive simulations demonstrate that DRMARL achieves robust chute mapping in the presence of varying induction distributions, reducing package recirculation by an average of 80\% in the simulation scenario.
Lifelong Multi-Agent Path Finding in Large-Scale Warehouses
May 15, 2020

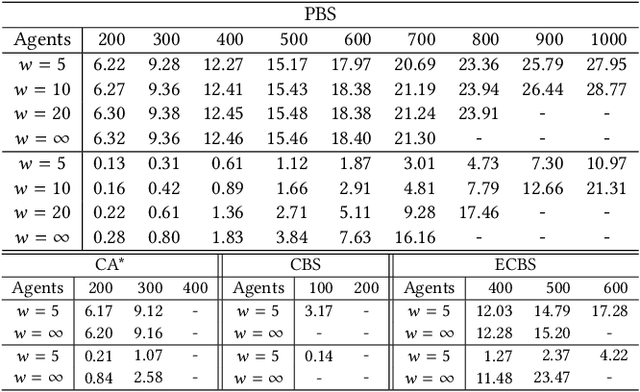
Abstract:Multi-Agent Path Finding (MAPF) is the problem of moving a team of agents to their goal locations without collisions. In this paper, we study the lifelong variant of MAPF where agents are constantly engaged with new goal locations, such as in large-scale warehouses. We propose a new framework for solving lifelong MAPF by decomposing the problem into a sequence of Windowed MAPF instances, where a Windowed MAPF solver resolves collisions among the paths of the agents only within a finite time horizon and ignores collisions beyond it. Our framework is particularly well suited to generating pliable plans that adapt to continually arriving new goal locations. Theoretically, we analyze the advantages and disadvantages of our framework. Empirically, we evaluate our framework with a variety of MAPF solvers and show that it can produce high-quality solutions for up to 1,000 agents, significantly outperforming existing methods.
The ACRV Picking Benchmark : A Robotic Shelf Picking Benchmark to Foster Reproducible Research
Dec 14, 2016



Abstract:Robotic challenges like the Amazon Picking Challenge (APC) or the DARPA Challenges are an established and important way to drive scientific progress. They make research comparable on a well-defined benchmark with equal test conditions for all participants. However, such challenge events occur only occasionally, are limited to a small number of contestants, and the test conditions are very difficult to replicate after the main event. We present a new physical benchmark challenge for robotic picking: the ACRV Picking Benchmark (APB). Designed to be reproducible, it consists of a set of 42 common objects, a widely available shelf, and exact guidelines for object arrangement using stencils. A well-defined evaluation protocol enables the comparison of \emph{complete} robotic systems -- including perception and manipulation -- instead of sub-systems only. Our paper also describes and reports results achieved by an open baseline system based on a Baxter robot.
Discrete Partitioning and Coverage Control for Gossiping Robots
Sep 26, 2011



Abstract:We propose distributed algorithms to automatically deploy a team of mobile robots to partition and provide coverage of a non-convex environment. To handle arbitrary non-convex environments, we represent them as graphs. Our partitioning and coverage algorithm requires only short-range, unreliable pairwise "gossip" communication. The algorithm has two components: (1) a motion protocol to ensure that neighboring robots communicate at least sporadically, and (2) a pairwise partitioning rule to update territory ownership when two robots communicate. By studying an appropriate dynamical system on the space of partitions of the graph vertices, we prove that territory ownership converges to a pairwise-optimal partition in finite time. This new equilibrium set represents improved performance over common Lloyd-type algorithms. Additionally, we detail how our algorithm scales well for large teams in large environments and how the computation can run in anytime with limited resources. Finally, we report on large-scale simulations in complex environments and hardware experiments using the Player/Stage robot control system.
Pairwise Optimal Discrete Coverage Control for Gossiping Robots
Aug 29, 2010


Abstract:We propose distributed algorithms to automatically deploy a group of robotic agents and provide coverage of a discretized environment represented by a graph. The classic Lloyd approach to coverage optimization involves separate centering and partitioning steps and converges to the set of centroidal Voronoi partitions. In this work we present a novel graph coverage algorithm which achieves better performance without this separation while requiring only pairwise ``gossip'' communication between agents. Our new algorithm provably converges to an element of the set of pairwise-optimal partitions, a subset of the set of centroidal Voronoi partitions. We illustrate that this new equilibrium set represents a significant performance improvement through numerical comparisons to existing Lloyd-type methods. Finally, we discuss ways to efficiently do the necessary computations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge