BiLO: Bilevel Local Operator Learning for PDE inverse problems

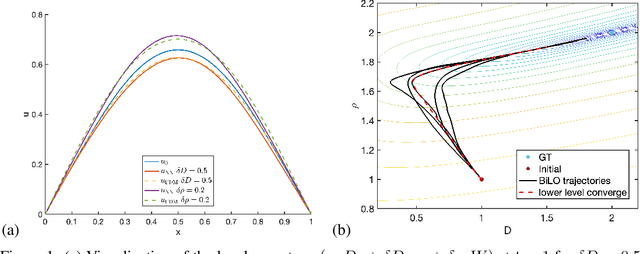
We propose a new neural network based method for solving inverse problems for partial differential equations (PDEs) by formulating the PDE inverse problem as a bilevel optimization problem. At the upper level, we minimize the data loss with respect to the PDE parameters. At the lower level, we train a neural network to locally approximate the PDE solution operator in the neighborhood of a given set of PDE parameters, which enables an accurate approximation of the descent direction for the upper level optimization problem. The lower level loss function includes the L2 norms of both the residual and its derivative with respect to the PDE parameters. We apply gradient descent simultaneously on both the upper and lower level optimization problems, leading to an effective and fast algorithm. The method, which we refer to as BiLO (Bilevel Local Operator learning), is also able to efficiently infer unknown functions in the PDEs through the introduction of an auxiliary variable. We demonstrate that our method enforces strong PDE constraints, is robust to sparse and noisy data, and eliminates the need to balance the residual and the data loss, which is inherent to soft PDE constraints.

Personalized Predictions of Glioblastoma Infiltration: Mathematical Models, Physics-Informed Neural Networks and Multimodal Scans

Predicting the infiltration of Glioblastoma (GBM) from medical MRI scans is crucial for understanding tumor growth dynamics and designing personalized radiotherapy treatment plans.Mathematical models of GBM growth can complement the data in the prediction of spatial distributions of tumor cells. However, this requires estimating patient-specific parameters of the model from clinical data, which is a challenging inverse problem due to limited temporal data and the limited time between imaging and diagnosis. This work proposes a method that uses Physics-Informed Neural Networks (PINNs) to estimate patient-specific parameters of a reaction-diffusion PDE model of GBM growth from a single 3D structural MRI snapshot. PINNs embed both the data and the PDE into a loss function, thus integrating theory and data. Key innovations include the identification and estimation of characteristic non-dimensional parameters, a pre-training step that utilizes the non-dimensional parameters and a fine-tuning step to determine the patient specific parameters. Additionally, the diffuse domain method is employed to handle the complex brain geometry within the PINN framework. Our method is validated both on synthetic and patient datasets, and shows promise for real-time parametric inference in the clinical setting for personalized GBM treatment.

The Liver Tumor Segmentation Benchmark (LiTS)

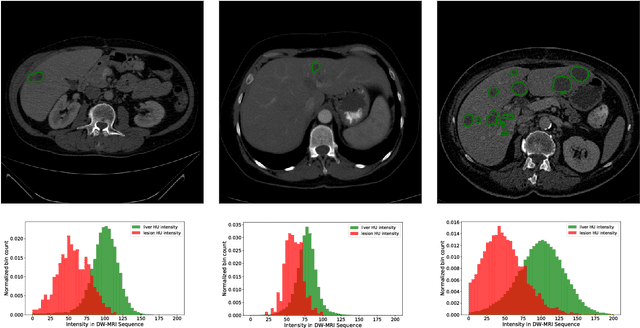
In this work, we report the set-up and results of the Liver Tumor Segmentation Benchmark (LITS) organized in conjunction with the IEEE International Symposium on Biomedical Imaging (ISBI) 2016 and International Conference On Medical Image Computing Computer Assisted Intervention (MICCAI) 2017. Twenty four valid state-of-the-art liver and liver tumor segmentation algorithms were applied to a set of 131 computed tomography (CT) volumes with different types of tumor contrast levels (hyper-/hypo-intense), abnormalities in tissues (metastasectomie) size and varying amount of lesions. The submitted algorithms have been tested on 70 undisclosed volumes. The dataset is created in collaboration with seven hospitals and research institutions and manually reviewed by independent three radiologists. We found that not a single algorithm performed best for liver and tumors. The best liver segmentation algorithm achieved a Dice score of 0.96(MICCAI) whereas for tumor segmentation the best algorithm evaluated at 0.67(ISBI) and 0.70(MICCAI). The LITS image data and manual annotations continue to be publicly available through an online evaluation system as an ongoing benchmarking resource.

Automated Unsupervised Segmentation of Liver Lesions in CT scans via Cahn-Hilliard Phase Separation

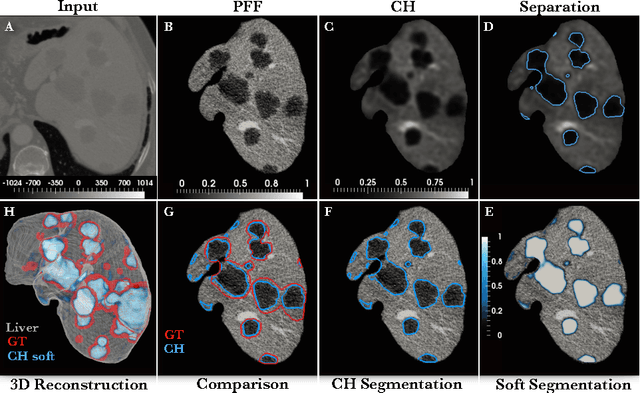
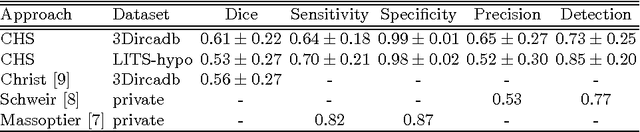
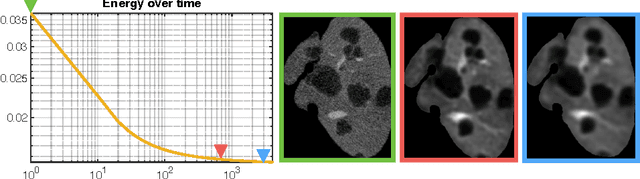
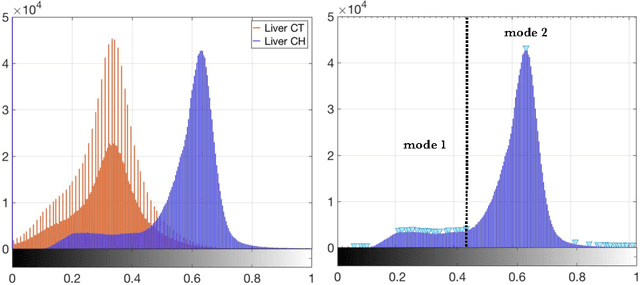
The segmentation of liver lesions is crucial for detection, diagnosis and monitoring progression of liver cancer. However, design of accurate automated methods remains challenging due to high noise in CT scans, low contrast between liver and lesions, as well as large lesion variability. We propose a 3D automatic, unsupervised method for liver lesions segmentation using a phase separation approach. It is assumed that liver is a mixture of two phases: healthy liver and lesions, represented by different image intensities polluted by noise. The Cahn-Hilliard equation is used to remove the noise and separate the mixture into two distinct phases with well-defined interfaces. This simplifies the lesion detection and segmentation task drastically and enables to segment liver lesions by thresholding the Cahn-Hilliard solution. The method was tested on 3Dircadb and LITS dataset.

POPE: Post Optimization Posterior Evaluation of Likelihood Free Models

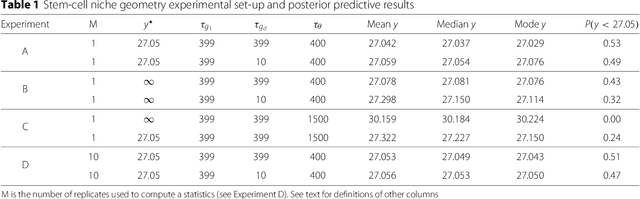
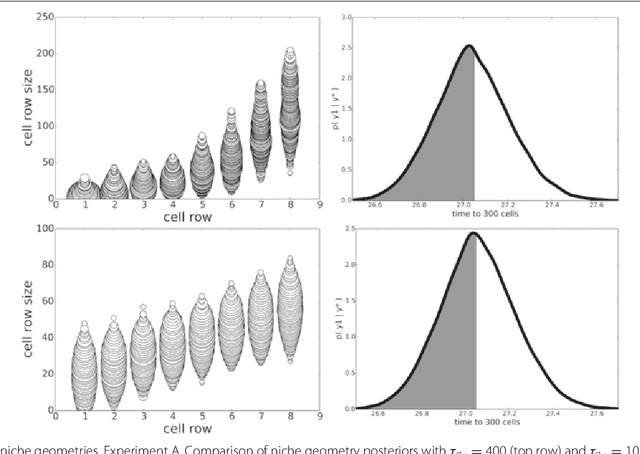
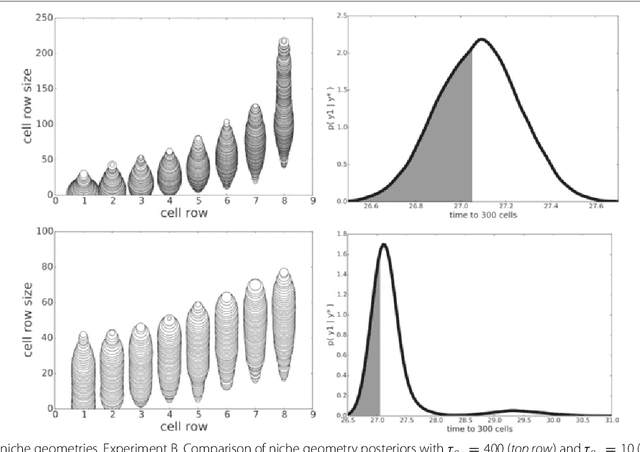
In many domains, scientists build complex simulators of natural phenomena that encode their hypotheses about the underlying processes. These simulators can be deterministic or stochastic, fast or slow, constrained or unconstrained, and so on. Optimizing the simulators with respect to a set of parameter values is common practice, resulting in a single parameter setting that minimizes an objective subject to constraints. We propose a post optimization posterior analysis that computes and visualizes all the models that can generate equally good or better simulation results, subject to constraints. These optimization posteriors are desirable for a number of reasons among which easy interpretability, automatic parameter sensitivity and correlation analysis and posterior predictive analysis. We develop a new sampling framework based on approximate Bayesian computation (ABC) with one-sided kernels. In collaboration with two groups of scientists we applied POPE to two important biological simulators: a fast and stochastic simulator of stem-cell cycling and a slow and deterministic simulator of tumor growth patterns.