Michael Chiang
POPE: Post Optimization Posterior Evaluation of Likelihood Free Models
Dec 09, 2014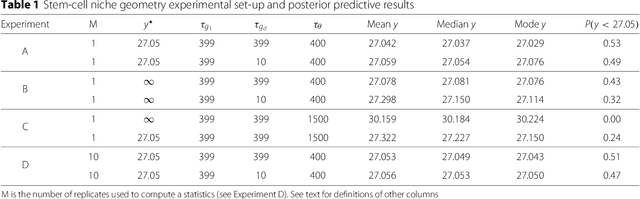
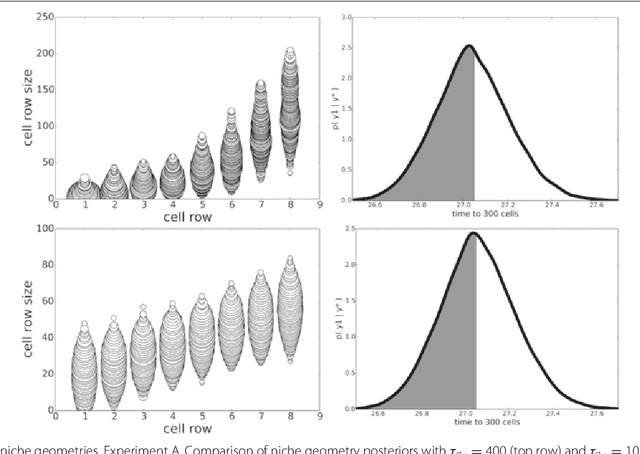
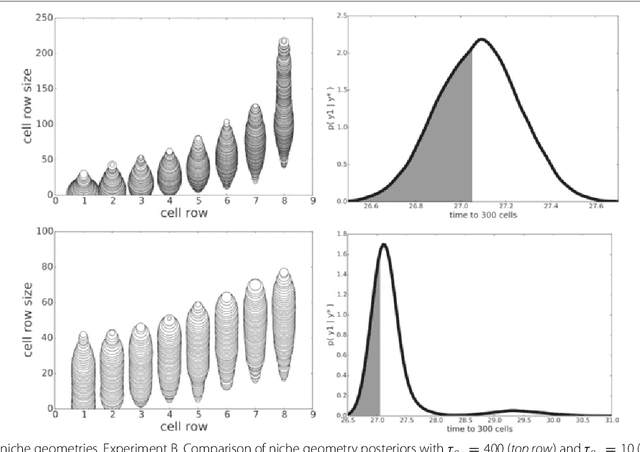
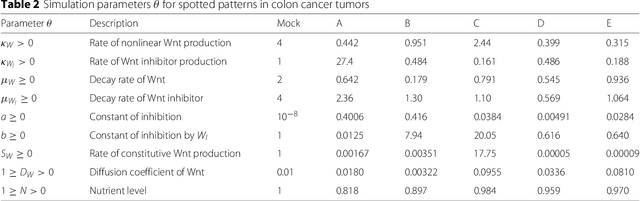
Abstract:In many domains, scientists build complex simulators of natural phenomena that encode their hypotheses about the underlying processes. These simulators can be deterministic or stochastic, fast or slow, constrained or unconstrained, and so on. Optimizing the simulators with respect to a set of parameter values is common practice, resulting in a single parameter setting that minimizes an objective subject to constraints. We propose a post optimization posterior analysis that computes and visualizes all the models that can generate equally good or better simulation results, subject to constraints. These optimization posteriors are desirable for a number of reasons among which easy interpretability, automatic parameter sensitivity and correlation analysis and posterior predictive analysis. We develop a new sampling framework based on approximate Bayesian computation (ABC) with one-sided kernels. In collaboration with two groups of scientists we applied POPE to two important biological simulators: a fast and stochastic simulator of stem-cell cycling and a slow and deterministic simulator of tumor growth patterns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge