Efficient Antibody Structure Refinement Using Energy-Guided SE(3) Flow Matching

Antibodies are proteins produced by the immune system that recognize and bind to specific antigens, and their 3D structures are crucial for understanding their binding mechanism and designing therapeutic interventions. The specificity of antibody-antigen binding predominantly depends on the complementarity-determining regions (CDR) within antibodies. Despite recent advancements in antibody structure prediction, the quality of predicted CDRs remains suboptimal. In this paper, we develop a novel antibody structure refinement method termed FlowAB based on energy-guided flow matching. FlowAB adopts the powerful deep generative method SE(3) flow matching and simultaneously incorporates important physical prior knowledge into the flow model to guide the generation process. The extensive experiments demonstrate that FlowAB can significantly improve the antibody CDR structures. It achieves new state-of-the-art performance on the antibody structure prediction task when used in conjunction with an appropriate prior model while incurring only marginal computational overhead. This advantage makes FlowAB a practical tool in antibody engineering.

SubGDiff: A Subgraph Diffusion Model to Improve Molecular Representation Learning

Molecular representation learning has shown great success in advancing AI-based drug discovery. The core of many recent works is based on the fact that the 3D geometric structure of molecules provides essential information about their physical and chemical characteristics. Recently, denoising diffusion probabilistic models have achieved impressive performance in 3D molecular representation learning. However, most existing molecular diffusion models treat each atom as an independent entity, overlooking the dependency among atoms within the molecular substructures. This paper introduces a novel approach that enhances molecular representation learning by incorporating substructural information within the diffusion process. We propose a novel diffusion model termed SubGDiff for involving the molecular subgraph information in diffusion. Specifically, SubGDiff adopts three vital techniques: i) subgraph prediction, ii) expectation state, and iii) k-step same subgraph diffusion, to enhance the perception of molecular substructure in the denoising network. Experimentally, extensive downstream tasks demonstrate the superior performance of our approach. The code is available at https://github.com/youjibiying/SubGDiff.

A Simple Hypergraph Kernel Convolution based on Discounted Markov Diffusion Process

Kernels on discrete structures evaluate pairwise similarities between objects which capture semantics and inherent topology information. Existing kernels on discrete structures are only developed by topology information(such as adjacency matrix of graphs), without considering original attributes of objects. This paper proposes a two-phase paradigm to aggregate comprehensive information on discrete structures leading to a Discount Markov Diffusion Learnable Kernel (DMDLK). Specifically, based on the underlying projection of DMDLK, we design a Simple Hypergraph Kernel Convolution (SHKC) for hidden representation of vertices. SHKC can adjust diffusion steps rather than stacking convolution layers to aggregate information from long-range neighborhoods which prevents over-smoothing issues of existing hypergraph convolutions. Moreover, we utilize the uniform stability bound theorem in transductive learning to analyze critical factors for the effectiveness and generalization ability of SHKC from a theoretical perspective. The experimental results on several benchmark datasets for node classification tasks verified the superior performance of SHKC over state-of-the-art methods.

GraphTTA: Test Time Adaptation on Graph Neural Networks

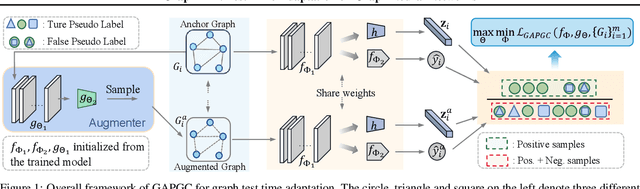
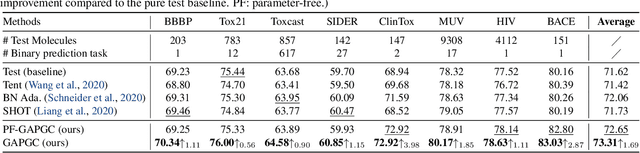
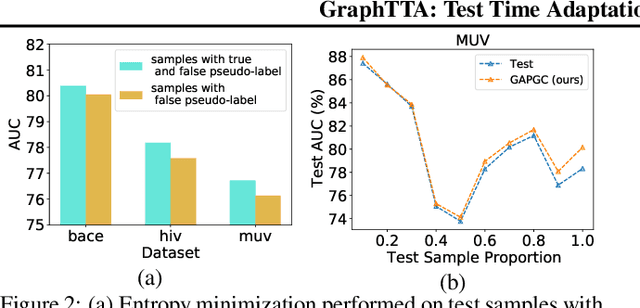
Recently, test time adaptation (TTA) has attracted increasing attention due to its power of handling the distribution shift issue in the real world. Unlike what has been developed for convolutional neural networks (CNNs) for image data, TTA is less explored for Graph Neural Networks (GNNs). There is still a lack of efficient algorithms tailored for graphs with irregular structures. In this paper, we present a novel test time adaptation strategy named Graph Adversarial Pseudo Group Contrast (GAPGC), for graph neural networks TTA, to better adapt to the Out Of Distribution (OOD) test data. Specifically, GAPGC employs a contrastive learning variant as a self-supervised task during TTA, equipped with Adversarial Learnable Augmenter and Group Pseudo-Positive Samples to enhance the relevance between the self-supervised task and the main task, boosting the performance of the main task. Furthermore, we provide theoretical evidence that GAPGC can extract minimal sufficient information for the main task from information theory perspective. Extensive experiments on molecular scaffold OOD dataset demonstrated that the proposed approach achieves state-of-the-art performance on GNNs.

Hypergraph Convolutional Networks via Equivalency between Hypergraphs and Undirected Graphs

As a powerful tool for modeling complex relationships, hypergraphs are gaining popularity from the graph learning community. However, commonly used frameworks in deep hypergraph learning focus on hypergraphs with \textit{edge-independent vertex weights}(EIVWs), without considering hypergraphs with \textit{edge-dependent vertex weights} (EDVWs) that have more modeling power. To compensate for this, in this paper, we present General Hypergraph Spectral Convolution(GHSC), a general learning framework that not only can handle EDVW and EIVW hypergraphs, but more importantly, enables theoretically explicitly utilizing the existing powerful Graph Convolutional Neural Networks (GCNNs) such that largely ease the design of Hypergraph Neural Networks. In this framework, the graph Laplacian of the given undirected GCNNs is replaced with a unified hypergraph Laplacian that incorporates vertex weight information from a random walk perspective by equating our defined generalized hypergraphs with simple undirected graphs. Extensive experiments from various domains including social network analysis, visual objective classification, protein learning demonstrate that the proposed framework can achieve state-of-the-art performance.

Preventing Over-Smoothing for Hypergraph Neural Networks

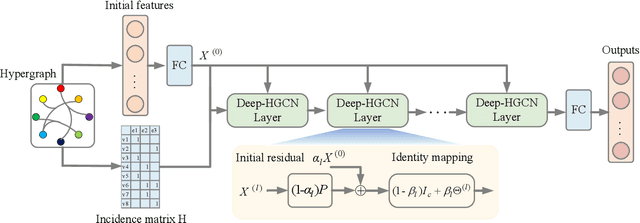
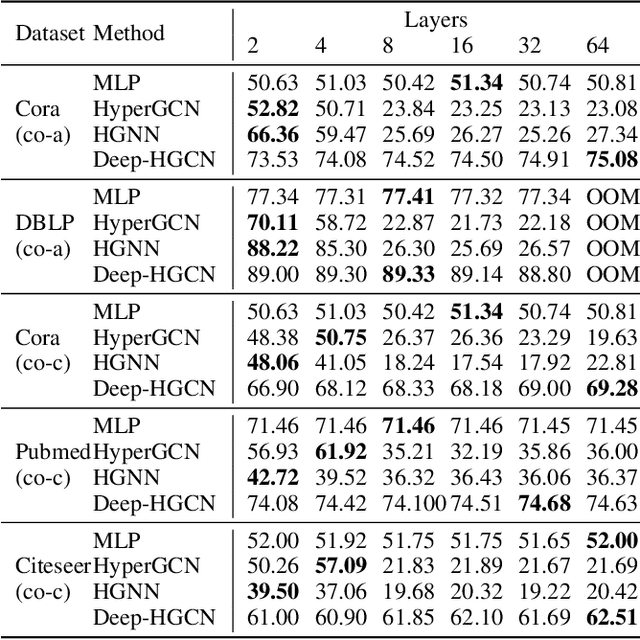
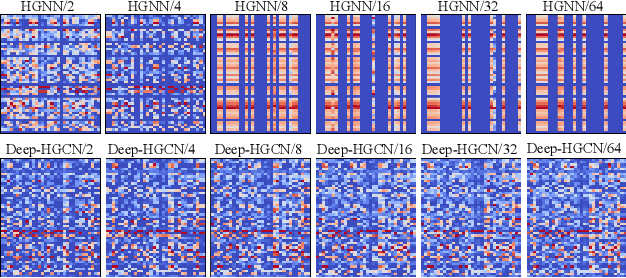
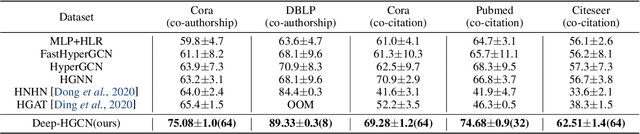
In recent years, hypergraph learning has attracted great attention due to its capacity in representing complex and high-order relationships. However, current neural network approaches designed for hypergraphs are mostly shallow, thus limiting their ability to extract information from high-order neighbors. In this paper, we show both theoretically and empirically, that the performance of hypergraph neural networks does not improve as the number of layers increases, which is known as the over-smoothing problem. To tackle this issue, we develop a new deep hypergraph convolutional network called Deep-HGCN, which can maintain the heterogeneity of node representation in deep layers. Specifically, we prove that a $k$-layer Deep-HGCN simulates a polynomial filter of order $k$ with arbitrary coefficients, which can relieve the problem of over-smoothing. Experimental results on various datasets demonstrate the superior performance of the proposed model comparing to the state-of-the-art hypergraph learning approaches.

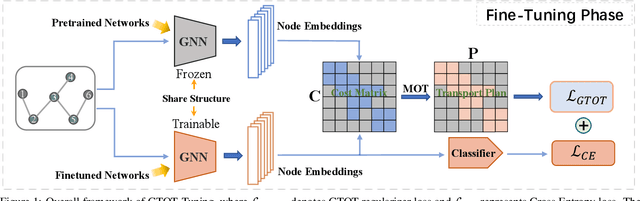
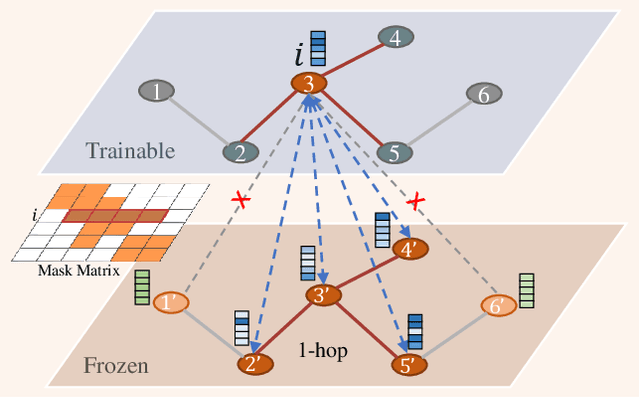
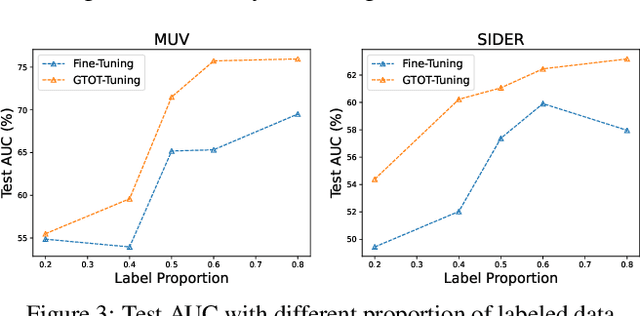
Fine-Tuning Graph Neural Networks via Graph Topology induced Optimal Transport

Recently, the pretrain-finetuning paradigm has attracted tons of attention in graph learning community due to its power of alleviating the lack of labels problem in many real-world applications. Current studies use existing techniques, such as weight constraint, representation constraint, which are derived from images or text data, to transfer the invariant knowledge from the pre-train stage to fine-tuning stage. However, these methods failed to preserve invariances from graph structure and Graph Neural Network (GNN) style models. In this paper, we present a novel optimal transport-based fine-tuning framework called GTOT-Tuning, namely, Graph Topology induced Optimal Transport fine-Tuning, for GNN style backbones. GTOT-Tuning is required to utilize the property of graph data to enhance the preservation of representation produced by fine-tuned networks. Toward this goal, we formulate graph local knowledge transfer as an Optimal Transport (OT) problem with a structural prior and construct the GTOT regularizer to constrain the fine-tuned model behaviors. By using the adjacency relationship amongst nodes, the GTOT regularizer achieves node-level optimal transport procedures and reduces redundant transport procedures, resulting in efficient knowledge transfer from the pre-trained models. We evaluate GTOT-Tuning on eight downstream tasks with various GNN backbones and demonstrate that it achieves state-of-the-art fine-tuning performance for GNNs.

Learnable Hypergraph Laplacian for Hypergraph Learning

HyperGraph Convolutional Neural Networks (HGCNNs) have demonstrated their potential in modeling high-order relations preserved in graph structured data. However, most existing convolution filters are localized and determined by the pre-defined initial hypergraph topology, neglecting to explore implicit and long-ange relations in real-world data. In this paper, we propose the first learning-based method tailored for constructing adaptive hypergraph structure, termed HypERgrAph Laplacian aDaptor (HERALD), which serves as a generic plug-in-play module for improving the representational power of HGCNNs. Specifically, HERALD adaptively optimizes the adjacency relationship between hypernodes and hyperedges in an end-to-end manner and thus the task-aware hypergraph is learned. Furthermore, HERALD employs the self-attention mechanism to capture the non-local paired-nodes relation. Extensive experiments on various popular hypergraph datasets for node classification and graph classification tasks demonstrate that our approach obtains consistent and considerable performance enhancement, proving its effectiveness and generalization ability.

Diversified Multiscale Graph Learning with Graph Self-Correction

Though the multiscale graph learning techniques have enabled advanced feature extraction frameworks, the classic ensemble strategy may show inferior performance while encountering the high homogeneity of the learnt representation, which is caused by the nature of existing graph pooling methods. To cope with this issue, we propose a diversified multiscale graph learning model equipped with two core ingredients: a graph self-correction (GSC) mechanism to generate informative embedded graphs, and a diversity boosting regularizer (DBR) to achieve a comprehensive characterization of the input graph. The proposed GSC mechanism compensates the pooled graph with the lost information during the graph pooling process by feeding back the estimated residual graph, which serves as a plug-in component for popular graph pooling methods. Meanwhile, pooling methods enhanced with the GSC procedure encourage the discrepancy of node embeddings, and thus it contributes to the success of ensemble learning strategy. The proposed DBR instead enhances the ensemble diversity at the graph-level embeddings by leveraging the interaction among individual classifiers. Extensive experiments on popular graph classification benchmarks show that the proposed GSC mechanism leads to significant improvements over state-of-the-art graph pooling methods. Moreover, the ensemble multiscale graph learning models achieve superior enhancement by combining both GSC and DBR.