Preventing Over-Smoothing for Hypergraph Neural Networks

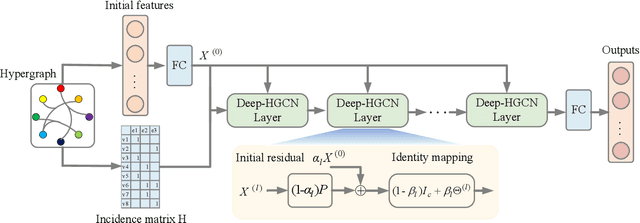
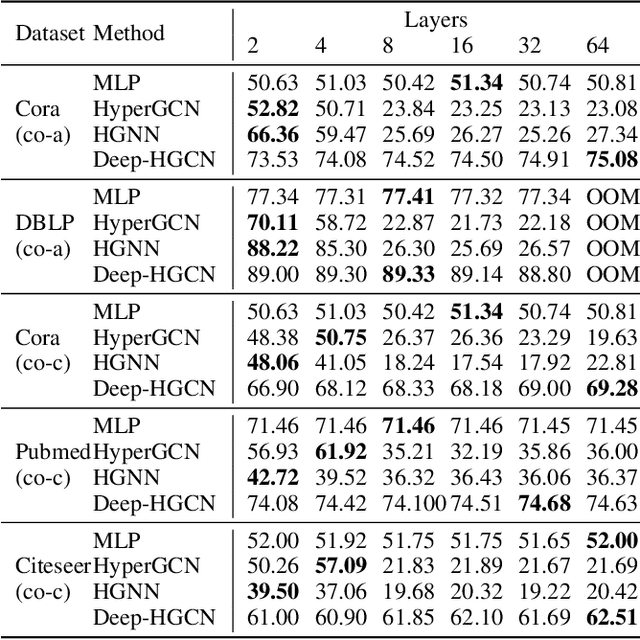
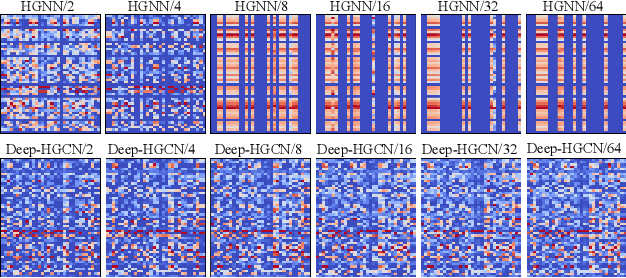
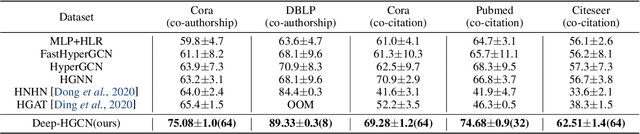
In recent years, hypergraph learning has attracted great attention due to its capacity in representing complex and high-order relationships. However, current neural network approaches designed for hypergraphs are mostly shallow, thus limiting their ability to extract information from high-order neighbors. In this paper, we show both theoretically and empirically, that the performance of hypergraph neural networks does not improve as the number of layers increases, which is known as the over-smoothing problem. To tackle this issue, we develop a new deep hypergraph convolutional network called Deep-HGCN, which can maintain the heterogeneity of node representation in deep layers. Specifically, we prove that a $k$-layer Deep-HGCN simulates a polynomial filter of order $k$ with arbitrary coefficients, which can relieve the problem of over-smoothing. Experimental results on various datasets demonstrate the superior performance of the proposed model comparing to the state-of-the-art hypergraph learning approaches.