LANTERN: Accelerating Visual Autoregressive Models with Relaxed Speculative Decoding

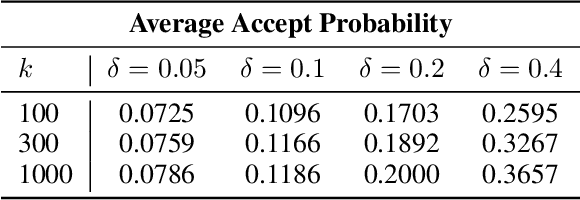
Auto-Regressive (AR) models have recently gained prominence in image generation, often matching or even surpassing the performance of diffusion models. However, one major limitation of AR models is their sequential nature, which processes tokens one at a time, slowing down generation compared to models like GANs or diffusion-based methods that operate more efficiently. While speculative decoding has proven effective for accelerating LLMs by generating multiple tokens in a single forward, its application in visual AR models remains largely unexplored. In this work, we identify a challenge in this setting, which we term \textit{token selection ambiguity}, wherein visual AR models frequently assign uniformly low probabilities to tokens, hampering the performance of speculative decoding. To overcome this challenge, we propose a relaxed acceptance condition referred to as LANTERN that leverages the interchangeability of tokens in latent space. This relaxation restores the effectiveness of speculative decoding in visual AR models by enabling more flexible use of candidate tokens that would otherwise be prematurely rejected. Furthermore, by incorporating a total variation distance bound, we ensure that these speed gains are achieved without significantly compromising image quality or semantic coherence. Experimental results demonstrate the efficacy of our method in providing a substantial speed-up over speculative decoding. In specific, compared to a na\"ive application of the state-of-the-art speculative decoding, LANTERN increases speed-ups by $\mathbf{1.75}\times$ and $\mathbf{1.76}\times$, as compared to greedy decoding and random sampling, respectively, when applied to LlamaGen, a contemporary visual AR model.

TEDDY: Trimming Edges with Degree-based Discrimination strategY

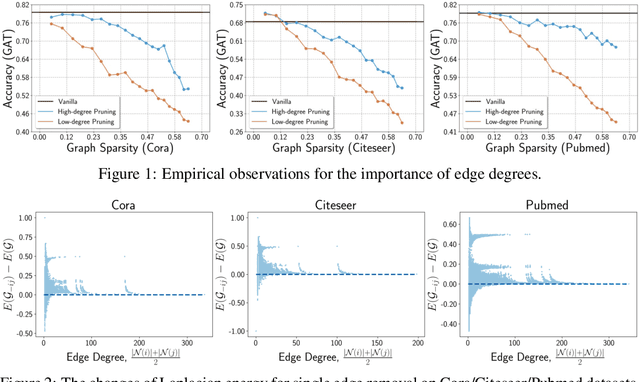
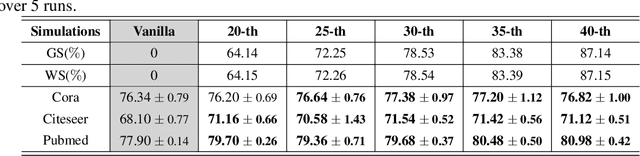
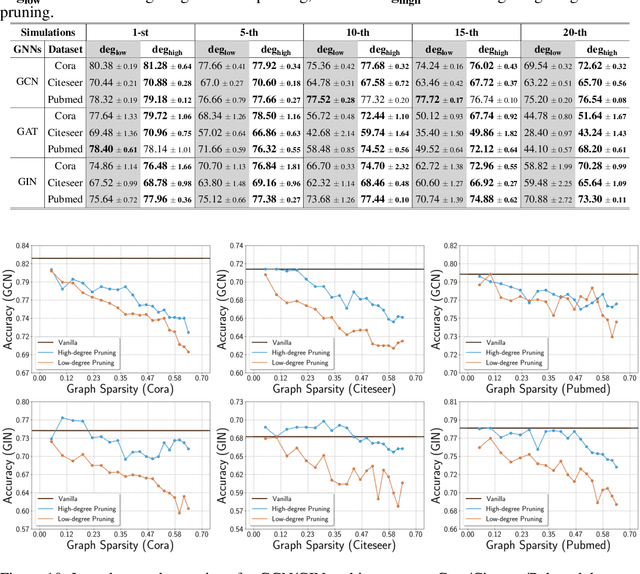
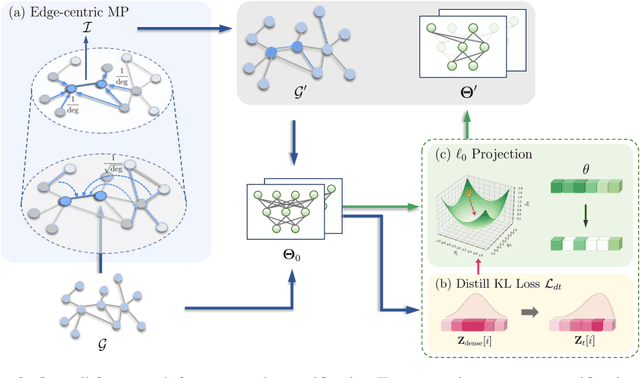
Since the pioneering work on the lottery ticket hypothesis for graph neural networks (GNNs) was proposed in Chen et al. (2021), the study on finding graph lottery tickets (GLT) has become one of the pivotal focus in the GNN community, inspiring researchers to discover sparser GLT while achieving comparable performance to original dense networks. In parallel, the graph structure has gained substantial attention as a crucial factor in GNN training dynamics, also elucidated by several recent studies. Despite this, contemporary studies on GLT, in general, have not fully exploited inherent pathways in the graph structure and identified tickets in an iterative manner, which is time-consuming and inefficient. To address these limitations, we introduce TEDDY, a one-shot edge sparsification framework that leverages structural information by incorporating edge-degree information. Following edge sparsification, we encourage the parameter sparsity during training via simple projected gradient descent on the $\ell_0$ ball. Given the target sparsity levels for both the graph structure and the model parameters, our TEDDY facilitates efficient and rapid realization of GLT within a single training. Remarkably, our experimental results demonstrate that TEDDY significantly surpasses conventional iterative approaches in generalization, even when conducting one-shot sparsification that solely utilizes graph structures, without taking node features into account.

Cluster-Promoting Quantization with Bit-Drop for Minimizing Network Quantization Loss

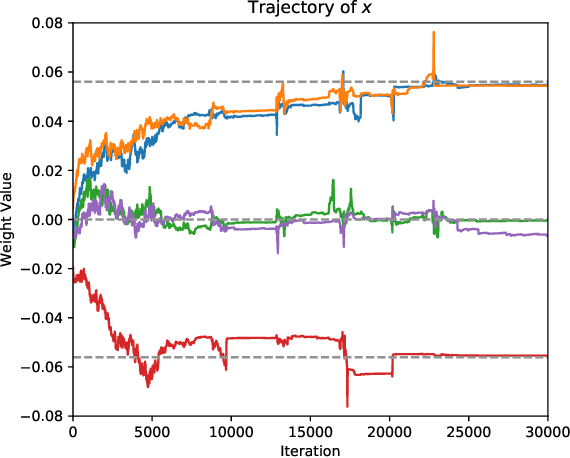
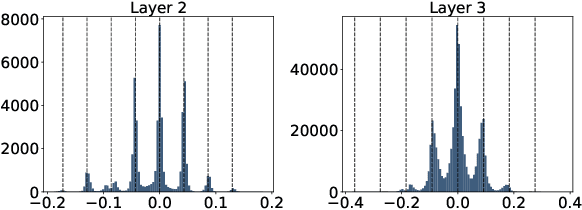
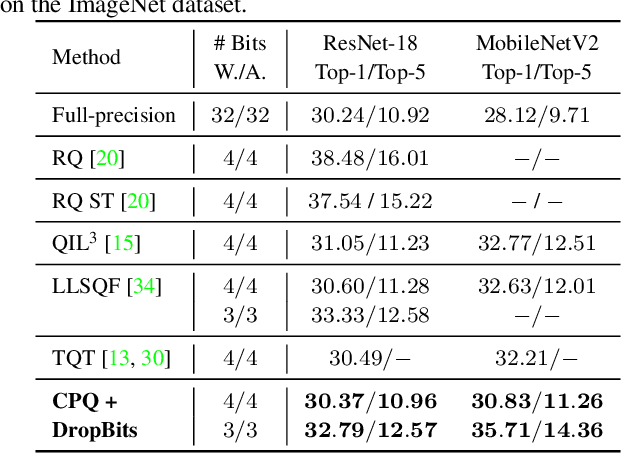
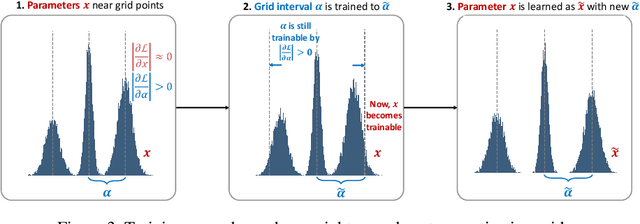
Network quantization, which aims to reduce the bit-lengths of the network weights and activations, has emerged for their deployments to resource-limited devices. Although recent studies have successfully discretized a full-precision network, they still incur large quantization errors after training, thus giving rise to a significant performance gap between a full-precision network and its quantized counterpart. In this work, we propose a novel quantization method for neural networks, Cluster-Promoting Quantization (CPQ) that finds the optimal quantization grids while naturally encouraging the underlying full-precision weights to gather around those quantization grids cohesively during training. This property of CPQ is thanks to our two main ingredients that enable differentiable quantization: i) the use of the categorical distribution designed by a specific probabilistic parametrization in the forward pass and ii) our proposed multi-class straight-through estimator (STE) in the backward pass. Since our second component, multi-class STE, is intrinsically biased, we additionally propose a new bit-drop technique, DropBits, that revises the standard dropout regularization to randomly drop bits instead of neurons. As a natural extension of DropBits, we further introduce the way of learning heterogeneous quantization levels to find proper bit-length for each layer by imposing an additional regularization on DropBits. We experimentally validate our method on various benchmark datasets and network architectures, and also support a new hypothesis for quantization: learning heterogeneous quantization levels outperforms the case using the same but fixed quantization levels from scratch.

A General Family of Stochastic Proximal Gradient Methods for Deep Learning

We study the training of regularized neural networks where the regularizer can be non-smooth and non-convex. We propose a unified framework for stochastic proximal gradient descent, which we term ProxGen, that allows for arbitrary positive preconditioners and lower semi-continuous regularizers. Our framework encompasses standard stochastic proximal gradient methods without preconditioners as special cases, which have been extensively studied in various settings. Not only that, we present two important update rules beyond the well-known standard methods as a byproduct of our approach: (i) the first closed-form proximal mappings of $\ell_q$ regularization ($0 \leq q \leq 1$) for adaptive stochastic gradient methods, and (ii) a revised version of ProxQuant that fixes a caveat of the original approach for quantization-specific regularizers. We analyze the convergence of ProxGen and show that the whole family of ProxGen enjoys the same convergence rate as stochastic proximal gradient descent without preconditioners. We also empirically show the superiority of proximal methods compared to subgradient-based approaches via extensive experiments. Interestingly, our results indicate that proximal methods with non-convex regularizers are more effective than those with convex regularizers.

Semi-Relaxed Quantization with DropBits: Training Low-Bit Neural Networks via Bit-wise Regularization

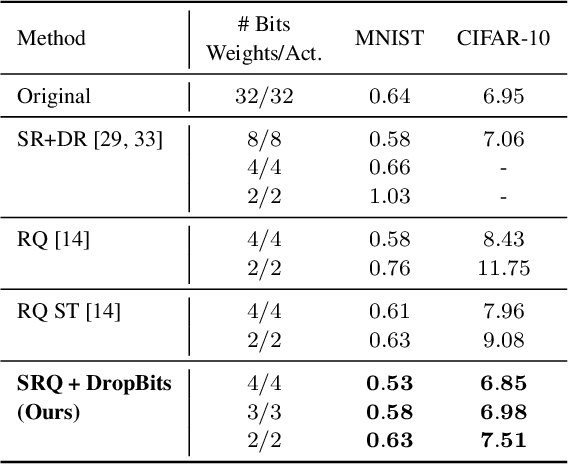
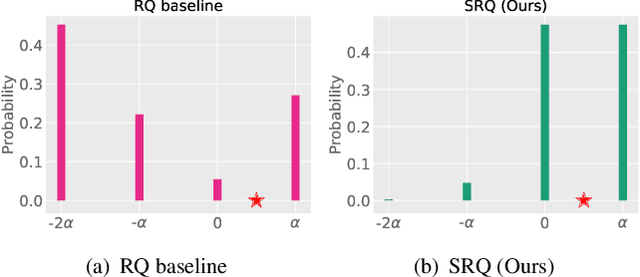
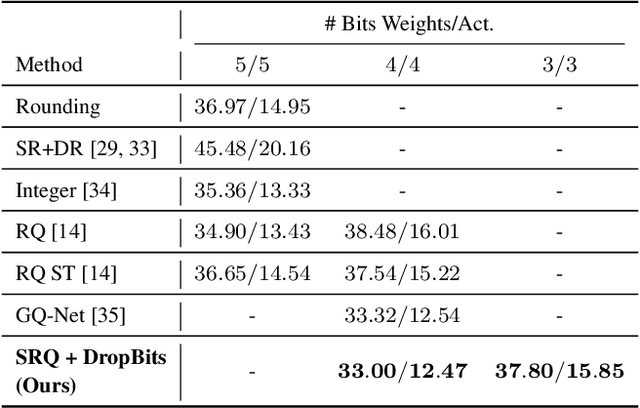
Neural Network quantization, which aims to reduce bit-lengths of the network weights and activations, is one of the key ingredients to reduce the size of neural networks for their deployments to resource-limited devices. However, compressing to low bit-lengths may incur large loss of information and preserving the performance of the full-precision networks under these settings is extremely challenging even with the state-of-the-art quantization approaches. To tackle this problem of low-bit quantization, we propose a novel Semi-Relaxed Quantization (SRQ) that can effectively reduce the quantization error, along with a new regularization technique, DropBits which replaces dropout regularization to randomly drop the bits instead of neurons to minimize information loss while improving generalization on low-bit networks. Moreover, we show the possibility of learning heterogeneous quantization levels, that finds proper bit-lengths for each layer using DropBits. We experimentally validate our method on various benchmark datasets and network architectures, whose results show that our method largely outperforms recent quantization approaches. To the best of our knowledge, we are the first in obtaining competitive performance on 3-bit quantization of ResNet-18 on ImageNet dataset with both weights and activations quantized, across all layers. Last but not the least, we show promising results on heterogeneous quantization, which we believe will open the door to new research directions in neural network quantization.

Stochastic Gradient Methods with Block Diagonal Matrix Adaptation

Adaptive gradient approaches that automatically adjust the learning rate on a per-feature basis have been very popular for training deep networks. This rich class of algorithms includes Adagrad, RMSprop, Adam, and recent extensions. All these algorithms have adopted diagonal matrix adaptation, due to the prohibitive computational burden of manipulating full matrices in high-dimensions. In this paper, we show that block-diagonal matrix adaptation can be a practical and powerful solution that can effectively utilize structural characteristics of deep learning architectures, and significantly improve convergence and out-of-sample generalization. We present a general framework with block-diagonal matrix updates via coordinate grouping, which includes counterparts of the aforementioned algorithms, prove their convergence in non-convex optimization, highlighting benefits compared to diagonal versions. In addition, we propose an efficient spectrum-clipping scheme that benefits from superior generalization performance of Sgd. Extensive experiments reveal that block-diagonal approaches achieve state-of-the-art results on several deep learning tasks, and can outperform adaptive diagonal methods, vanilla Sgd, as well as a modified version of full-matrix adaptation proposed very recently.