Unraveling Zeroth-Order Optimization through the Lens of Low-Dimensional Structured Perturbations

Zeroth-order (ZO) optimization has emerged as a promising alternative to gradient-based backpropagation methods, particularly for black-box optimization and large language model (LLM) fine-tuning. However, ZO methods suffer from slow convergence due to high-variance stochastic gradient estimators. While structured perturbations, such as sparsity and low-rank constraints, have been explored to mitigate these issues, their effectiveness remains highly under-explored. In this work, we develop a unified theoretical framework that analyzes both the convergence and generalization properties of ZO optimization under structured perturbations. We show that high dimensionality is the primary bottleneck and introduce the notions of \textit{stable rank} and \textit{effective overlap} to explain how structured perturbations reduce gradient noise and accelerate convergence. Using the uniform stability under our framework, we then provide the first theoretical justification for why these perturbations enhance generalization. Additionally, through empirical analysis, we identify that \textbf{block coordinate descent} (BCD) to be an effective structured perturbation method. Extensive experiments show that, compared to existing alternatives, memory-efficient ZO (MeZO) with BCD (\textit{MeZO-BCD}) can provide improved converge with a faster wall-clock time/iteration by up to $\times\textbf{2.09}$ while yielding similar or better accuracy.

Scale-invariant Bayesian Neural Networks with Connectivity Tangent Kernel

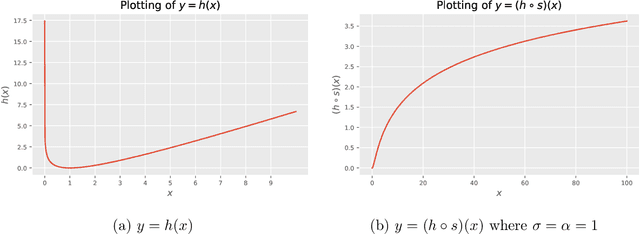
Explaining generalizations and preventing over-confident predictions are central goals of studies on the loss landscape of neural networks. Flatness, defined as loss invariability on perturbations of a pre-trained solution, is widely accepted as a predictor of generalization in this context. However, the problem that flatness and generalization bounds can be changed arbitrarily according to the scale of a parameter was pointed out, and previous studies partially solved the problem with restrictions: Counter-intuitively, their generalization bounds were still variant for the function-preserving parameter scaling transformation or limited only to an impractical network structure. As a more fundamental solution, we propose new prior and posterior distributions invariant to scaling transformations by \textit{decomposing} the scale and connectivity of parameters, thereby allowing the resulting generalization bound to describe the generalizability of a broad class of networks with the more practical class of transformations such as weight decay with batch normalization. We also show that the above issue adversely affects the uncertainty calibration of Laplace approximation and propose a solution using our invariant posterior. We empirically demonstrate our posterior provides effective flatness and calibration measures with low complexity in such a practical parameter transformation case, supporting its practical effectiveness in line with our rationale.