LANTERN++: Enhanced Relaxed Speculative Decoding with Static Tree Drafting for Visual Auto-regressive Models

Speculative decoding has been widely used to accelerate autoregressive (AR) text generation. However, its effectiveness in visual AR models remains limited due to token selection ambiguity, where multiple tokens receive similarly low probabilities, reducing acceptance rates. While dynamic tree drafting has been proposed to improve speculative decoding, we show that it fails to mitigate token selection ambiguity, resulting in shallow draft trees and suboptimal acceleration. To address this, we introduce LANTERN++, a novel framework that integrates static tree drafting with a relaxed acceptance condition, allowing drafts to be selected independently of low-confidence predictions. This enables deeper accepted sequences, improving decoding efficiency while preserving image quality. Extensive experiments on state-of-the-art visual AR models demonstrate that LANTERN++ significantly accelerates inference, achieving up to $\mathbf{\times 2.56}$ speedup over standard AR decoding while maintaining high image quality.

Unraveling Zeroth-Order Optimization through the Lens of Low-Dimensional Structured Perturbations

Zeroth-order (ZO) optimization has emerged as a promising alternative to gradient-based backpropagation methods, particularly for black-box optimization and large language model (LLM) fine-tuning. However, ZO methods suffer from slow convergence due to high-variance stochastic gradient estimators. While structured perturbations, such as sparsity and low-rank constraints, have been explored to mitigate these issues, their effectiveness remains highly under-explored. In this work, we develop a unified theoretical framework that analyzes both the convergence and generalization properties of ZO optimization under structured perturbations. We show that high dimensionality is the primary bottleneck and introduce the notions of \textit{stable rank} and \textit{effective overlap} to explain how structured perturbations reduce gradient noise and accelerate convergence. Using the uniform stability under our framework, we then provide the first theoretical justification for why these perturbations enhance generalization. Additionally, through empirical analysis, we identify that \textbf{block coordinate descent} (BCD) to be an effective structured perturbation method. Extensive experiments show that, compared to existing alternatives, memory-efficient ZO (MeZO) with BCD (\textit{MeZO-BCD}) can provide improved converge with a faster wall-clock time/iteration by up to $\times\textbf{2.09}$ while yielding similar or better accuracy.

LANTERN: Accelerating Visual Autoregressive Models with Relaxed Speculative Decoding

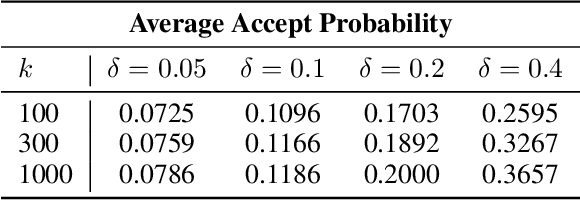
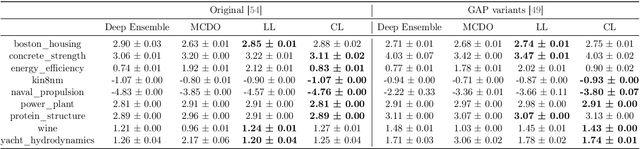
Auto-Regressive (AR) models have recently gained prominence in image generation, often matching or even surpassing the performance of diffusion models. However, one major limitation of AR models is their sequential nature, which processes tokens one at a time, slowing down generation compared to models like GANs or diffusion-based methods that operate more efficiently. While speculative decoding has proven effective for accelerating LLMs by generating multiple tokens in a single forward, its application in visual AR models remains largely unexplored. In this work, we identify a challenge in this setting, which we term \textit{token selection ambiguity}, wherein visual AR models frequently assign uniformly low probabilities to tokens, hampering the performance of speculative decoding. To overcome this challenge, we propose a relaxed acceptance condition referred to as LANTERN that leverages the interchangeability of tokens in latent space. This relaxation restores the effectiveness of speculative decoding in visual AR models by enabling more flexible use of candidate tokens that would otherwise be prematurely rejected. Furthermore, by incorporating a total variation distance bound, we ensure that these speed gains are achieved without significantly compromising image quality or semantic coherence. Experimental results demonstrate the efficacy of our method in providing a substantial speed-up over speculative decoding. In specific, compared to a na\"ive application of the state-of-the-art speculative decoding, LANTERN increases speed-ups by $\mathbf{1.75}\times$ and $\mathbf{1.76}\times$, as compared to greedy decoding and random sampling, respectively, when applied to LlamaGen, a contemporary visual AR model.

Scale-invariant Bayesian Neural Networks with Connectivity Tangent Kernel

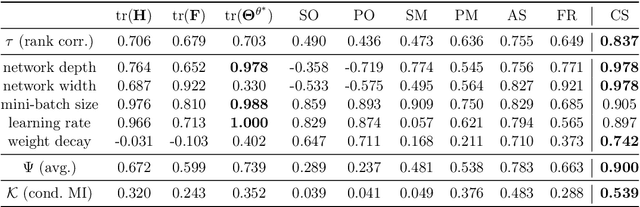
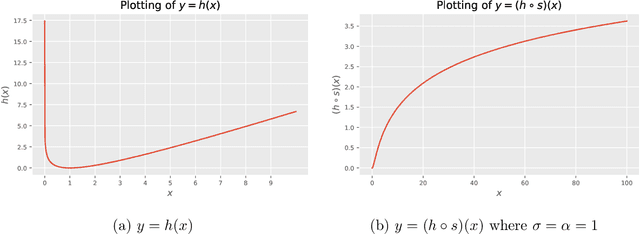
Explaining generalizations and preventing over-confident predictions are central goals of studies on the loss landscape of neural networks. Flatness, defined as loss invariability on perturbations of a pre-trained solution, is widely accepted as a predictor of generalization in this context. However, the problem that flatness and generalization bounds can be changed arbitrarily according to the scale of a parameter was pointed out, and previous studies partially solved the problem with restrictions: Counter-intuitively, their generalization bounds were still variant for the function-preserving parameter scaling transformation or limited only to an impractical network structure. As a more fundamental solution, we propose new prior and posterior distributions invariant to scaling transformations by \textit{decomposing} the scale and connectivity of parameters, thereby allowing the resulting generalization bound to describe the generalizability of a broad class of networks with the more practical class of transformations such as weight decay with batch normalization. We also show that the above issue adversely affects the uncertainty calibration of Laplace approximation and propose a solution using our invariant posterior. We empirically demonstrate our posterior provides effective flatness and calibration measures with low complexity in such a practical parameter transformation case, supporting its practical effectiveness in line with our rationale.