A General Family of Stochastic Proximal Gradient Methods for Deep Learning

We study the training of regularized neural networks where the regularizer can be non-smooth and non-convex. We propose a unified framework for stochastic proximal gradient descent, which we term ProxGen, that allows for arbitrary positive preconditioners and lower semi-continuous regularizers. Our framework encompasses standard stochastic proximal gradient methods without preconditioners as special cases, which have been extensively studied in various settings. Not only that, we present two important update rules beyond the well-known standard methods as a byproduct of our approach: (i) the first closed-form proximal mappings of $\ell_q$ regularization ($0 \leq q \leq 1$) for adaptive stochastic gradient methods, and (ii) a revised version of ProxQuant that fixes a caveat of the original approach for quantization-specific regularizers. We analyze the convergence of ProxGen and show that the whole family of ProxGen enjoys the same convergence rate as stochastic proximal gradient descent without preconditioners. We also empirically show the superiority of proximal methods compared to subgradient-based approaches via extensive experiments. Interestingly, our results indicate that proximal methods with non-convex regularizers are more effective than those with convex regularizers.

Stochastic Gradient Methods with Block Diagonal Matrix Adaptation

Adaptive gradient approaches that automatically adjust the learning rate on a per-feature basis have been very popular for training deep networks. This rich class of algorithms includes Adagrad, RMSprop, Adam, and recent extensions. All these algorithms have adopted diagonal matrix adaptation, due to the prohibitive computational burden of manipulating full matrices in high-dimensions. In this paper, we show that block-diagonal matrix adaptation can be a practical and powerful solution that can effectively utilize structural characteristics of deep learning architectures, and significantly improve convergence and out-of-sample generalization. We present a general framework with block-diagonal matrix updates via coordinate grouping, which includes counterparts of the aforementioned algorithms, prove their convergence in non-convex optimization, highlighting benefits compared to diagonal versions. In addition, we propose an efficient spectrum-clipping scheme that benefits from superior generalization performance of Sgd. Extensive experiments reveal that block-diagonal approaches achieve state-of-the-art results on several deep learning tasks, and can outperform adaptive diagonal methods, vanilla Sgd, as well as a modified version of full-matrix adaptation proposed very recently.

Removing Clouds and Recovering Ground Observations in Satellite Image Sequences via Temporally Contiguous Robust Matrix Completion

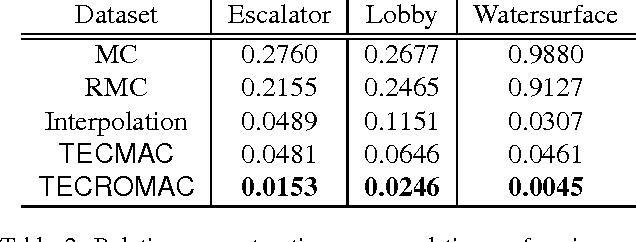
We consider the problem of removing and replacing clouds in satellite image sequences, which has a wide range of applications in remote sensing. Our approach first detects and removes the cloud-contaminated part of the image sequences. It then recovers the missing scenes from the clean parts using the proposed "TECROMAC" (TEmporally Contiguous RObust MAtrix Completion) objective. The objective function balances temporal smoothness with a low rank solution while staying close to the original observations. The matrix whose the rows are pixels and columnsare days corresponding to the image, has low-rank because the pixels reflect land-types such as vegetation, roads and lakes and there are relatively few variations as a result. We provide efficient optimization algorithms for TECROMAC, so we can exploit images containing millions of pixels. Empirical results on real satellite image sequences, as well as simulated data, demonstrate that our approach is able to recover underlying images from heavily cloud-contaminated observations.

Sparse Quantile Huber Regression for Efficient and Robust Estimation

We consider new formulations and methods for sparse quantile regression in the high-dimensional setting. Quantile regression plays an important role in many applications, including outlier-robust exploratory analysis in gene selection. In addition, the sparsity consideration in quantile regression enables the exploration of the entire conditional distribution of the response variable given the predictors and therefore yields a more comprehensive view of the important predictors. We propose a generalized OMP algorithm for variable selection, taking the misfit loss to be either the traditional quantile loss or a smooth version we call quantile Huber, and compare the resulting greedy approaches with convex sparsity-regularized formulations. We apply a recently proposed interior point methodology to efficiently solve all convex formulations as well as convex subproblems in the generalized OMP setting, pro- vide theoretical guarantees of consistent estimation, and demonstrate the performance of our approach using empirical studies of simulated and genomic datasets.

Scalable Matrix-valued Kernel Learning for High-dimensional Nonlinear Multivariate Regression and Granger Causality

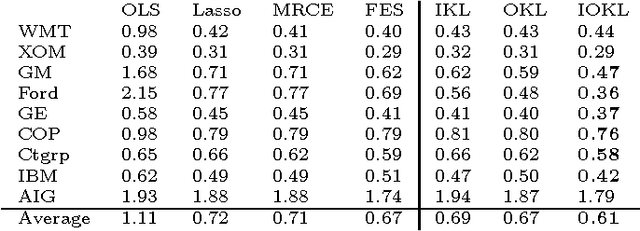
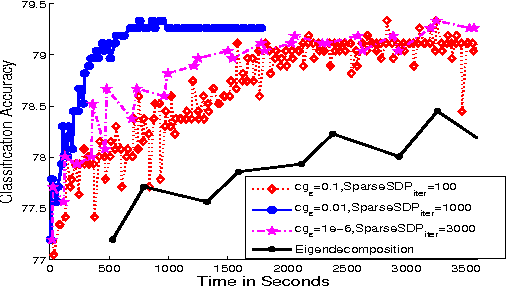
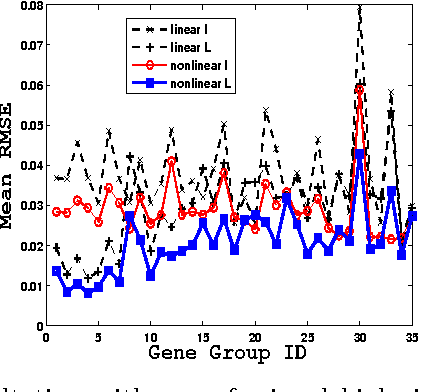
We propose a general matrix-valued multiple kernel learning framework for high-dimensional nonlinear multivariate regression problems. This framework allows a broad class of mixed norm regularizers, including those that induce sparsity, to be imposed on a dictionary of vector-valued Reproducing Kernel Hilbert Spaces. We develop a highly scalable and eigendecomposition-free algorithm that orchestrates two inexact solvers for simultaneously learning both the input and output components of separable matrix-valued kernels. As a key application enabled by our framework, we show how high-dimensional causal inference tasks can be naturally cast as sparse function estimation problems, leading to novel nonlinear extensions of a class of Graphical Granger Causality techniques. Our algorithmic developments and extensive empirical studies are complemented by theoretical analyses in terms of Rademacher generalization bounds.