Igor Gitman
Learning Generative Selection for Best-of-N
Feb 02, 2026Abstract:Scaling test-time compute via parallel sampling can substantially improve LLM reasoning, but is often limited by Best-of-N selection quality. Generative selection methods, such as GenSelect, address this bottleneck, yet strong selection performance remains largely limited to large models. We show that small reasoning models can acquire strong GenSelect capabilities through targeted reinforcement learning. To this end, we synthesize selection tasks from large-scale math and code instruction datasets by filtering to instances with both correct and incorrect candidate solutions, and train 1.7B-parameter models with DAPO to reward correct selections. Across math (AIME24, AIME25, HMMT25) and code (LiveCodeBench) reasoning benchmarks, our models consistently outperform prompting and majority-voting baselines, often approaching or exceeding much larger models. Moreover, these gains generalize to selecting outputs from stronger models despite training only on outputs from weaker models. Overall, our results establish reinforcement learning as a scalable way to unlock strong generative selection in small models, enabling efficient test-time scaling.
NVIDIA Nemotron 3: Efficient and Open Intelligence
Dec 24, 2025Abstract:We introduce the Nemotron 3 family of models - Nano, Super, and Ultra. These models deliver strong agentic, reasoning, and conversational capabilities. The Nemotron 3 family uses a Mixture-of-Experts hybrid Mamba-Transformer architecture to provide best-in-class throughput and context lengths of up to 1M tokens. Super and Ultra models are trained with NVFP4 and incorporate LatentMoE, a novel approach that improves model quality. The two larger models also include MTP layers for faster text generation. All Nemotron 3 models are post-trained using multi-environment reinforcement learning enabling reasoning, multi-step tool use, and support granular reasoning budget control. Nano, the smallest model, outperforms comparable models in accuracy while remaining extremely cost-efficient for inference. Super is optimized for collaborative agents and high-volume workloads such as IT ticket automation. Ultra, the largest model, provides state-of-the-art accuracy and reasoning performance. Nano is released together with its technical report and this white paper, while Super and Ultra will follow in the coming months. We will openly release the model weights, pre- and post-training software, recipes, and all data for which we hold redistribution rights.
Nemotron 3 Nano: Open, Efficient Mixture-of-Experts Hybrid Mamba-Transformer Model for Agentic Reasoning
Dec 23, 2025Abstract:We present Nemotron 3 Nano 30B-A3B, a Mixture-of-Experts hybrid Mamba-Transformer language model. Nemotron 3 Nano was pretrained on 25 trillion text tokens, including more than 3 trillion new unique tokens over Nemotron 2, followed by supervised fine tuning and large-scale RL on diverse environments. Nemotron 3 Nano achieves better accuracy than our previous generation Nemotron 2 Nano while activating less than half of the parameters per forward pass. It achieves up to 3.3x higher inference throughput than similarly-sized open models like GPT-OSS-20B and Qwen3-30B-A3B-Thinking-2507, while also being more accurate on popular benchmarks. Nemotron 3 Nano demonstrates enhanced agentic, reasoning, and chat abilities and supports context lengths up to 1M tokens. We release both our pretrained Nemotron 3 Nano 30B-A3B Base and post-trained Nemotron 3 Nano 30B-A3B checkpoints on Hugging Face.
Nemotron-Math: Efficient Long-Context Distillation of Mathematical Reasoning from Multi-Mode Supervision
Dec 17, 2025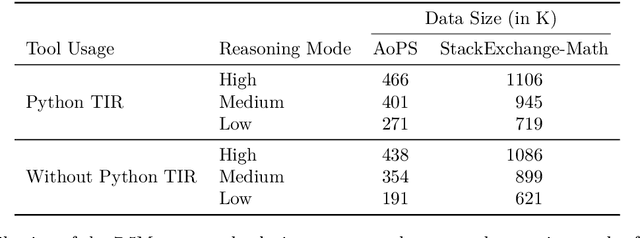
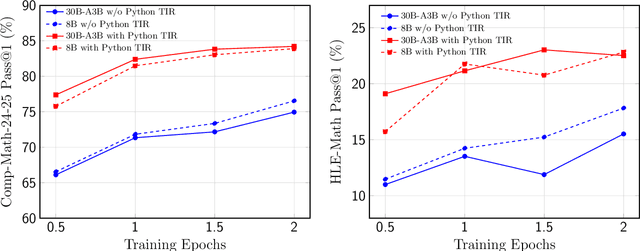

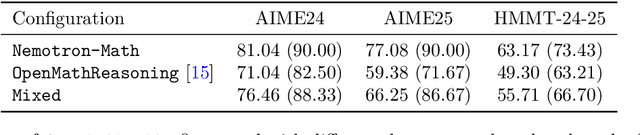
Abstract:High-quality mathematical reasoning supervision requires diverse reasoning styles, long-form traces, and effective tool integration, capabilities that existing datasets provide only in limited form. Leveraging the multi-mode generation ability of gpt-oss-120b, we introduce Nemotron-Math, a large-scale mathematical reasoning dataset containing 7.5M solution traces across high, medium, and low reasoning modes, each available both with and without Python tool-integrated reasoning (TIR). The dataset integrates 85K curated AoPS problems with 262K community-sourced StackExchange-Math problems, combining structured competition tasks with diverse real-world mathematical queries. We conduct controlled evaluations to assess the dataset quality. Nemotron-Math consistently outperforms the original OpenMathReasoning on matched AoPS problems. Incorporating StackExchange-Math substantially improves robustness and generalization, especially on HLE-Math, while preserving accuracy on math competition benchmarks. To support efficient long-context training, we develop a sequential bucketed strategy that accelerates 128K context-length fine-tuning by 2--3$\times$ without significant accuracy loss. Overall, Nemotron-Math enables state-of-the-art performance, including 100\% maj@16 accuracy on AIME 2024 and 2025 with Python TIR.
Scaling Generative Verifiers For Natural Language Mathematical Proof Verification And Selection
Nov 17, 2025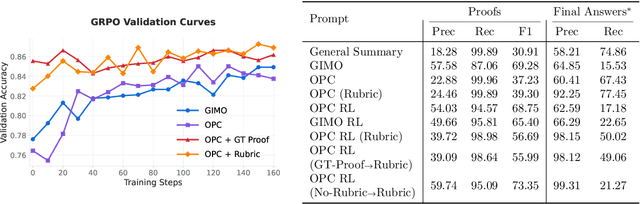
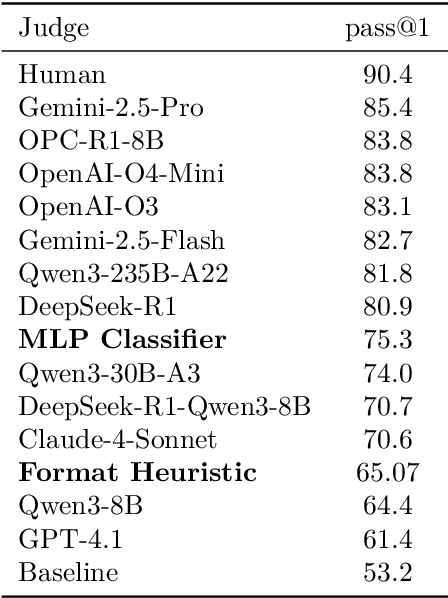
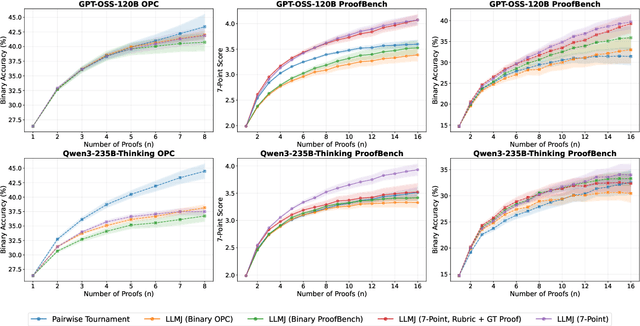

Abstract:Large language models have achieved remarkable success on final-answer mathematical problems, largely due to the ease of applying reinforcement learning with verifiable rewards. However, the reasoning underlying these solutions is often flawed. Advancing to rigorous proof-based mathematics requires reliable proof verification capabilities. We begin by analyzing multiple evaluation setups and show that focusing on a single benchmark can lead to brittle or misleading conclusions. To address this, we evaluate both proof-based and final-answer reasoning to obtain a more reliable measure of model performance. We then scale two major generative verification methods (GenSelect and LLM-as-a-Judge) to millions of tokens and identify their combination as the most effective framework for solution verification and selection. We further show that the choice of prompt for LLM-as-a-Judge significantly affects the model's performance, but reinforcement learning can reduce this sensitivity. However, despite improving proof-level metrics, reinforcement learning does not enhance final-answer precision, indicating that current models often reward stylistic or procedural correctness rather than mathematical validity. Our results establish practical guidelines for designing and evaluating scalable proof-verification and selection systems.
NVIDIA Nemotron Nano 2: An Accurate and Efficient Hybrid Mamba-Transformer Reasoning Model
Aug 21, 2025



Abstract:We introduce Nemotron-Nano-9B-v2, a hybrid Mamba-Transformer language model designed to increase throughput for reasoning workloads while achieving state-of-the-art accuracy compared to similarly-sized models. Nemotron-Nano-9B-v2 builds on the Nemotron-H architecture, in which the majority of the self-attention layers in the common Transformer architecture are replaced with Mamba-2 layers, to achieve improved inference speed when generating the long thinking traces needed for reasoning. We create Nemotron-Nano-9B-v2 by first pre-training a 12-billion-parameter model (Nemotron-Nano-12B-v2-Base) on 20 trillion tokens using an FP8 training recipe. After aligning Nemotron-Nano-12B-v2-Base, we employ the Minitron strategy to compress and distill the model with the goal of enabling inference on up to 128k tokens on a single NVIDIA A10G GPU (22GiB of memory, bfloat16 precision). Compared to existing similarly-sized models (e.g., Qwen3-8B), we show that Nemotron-Nano-9B-v2 achieves on-par or better accuracy on reasoning benchmarks while achieving up to 6x higher inference throughput in reasoning settings like 8k input and 16k output tokens. We are releasing Nemotron-Nano-9B-v2, Nemotron-Nano12B-v2-Base, and Nemotron-Nano-9B-v2-Base checkpoints along with the majority of our pre- and post-training datasets on Hugging Face.
GenSelect: A Generative Approach to Best-of-N
Jul 23, 2025Abstract:Generative reward models with parallel sampling have enabled effective test-time scaling for reasoning tasks. Current approaches employ pointwise scoring of individual solutions or pairwise comparisons. However, pointwise methods underutilize LLMs' comparative abilities, while pairwise methods scale inefficiently with larger sampling budgets. We introduce GenSelect, where the LLM uses long reasoning to select the best solution among N candidates. This leverages LLMs' comparative strengths while scaling efficiently across parallel sampling budgets. For math reasoning, we demonstrate that reasoning models, such as QwQ and DeepSeek-R1-0528, excel at GenSelect, outperforming existing scoring approaches with simple prompting.
Llama-Nemotron: Efficient Reasoning Models
May 02, 2025



Abstract:We introduce the Llama-Nemotron series of models, an open family of heterogeneous reasoning models that deliver exceptional reasoning capabilities, inference efficiency, and an open license for enterprise use. The family comes in three sizes -- Nano (8B), Super (49B), and Ultra (253B) -- and performs competitively with state-of-the-art reasoning models such as DeepSeek-R1 while offering superior inference throughput and memory efficiency. In this report, we discuss the training procedure for these models, which entails using neural architecture search from Llama 3 models for accelerated inference, knowledge distillation, and continued pretraining, followed by a reasoning-focused post-training stage consisting of two main parts: supervised fine-tuning and large scale reinforcement learning. Llama-Nemotron models are the first open-source models to support a dynamic reasoning toggle, allowing users to switch between standard chat and reasoning modes during inference. To further support open research and facilitate model development, we provide the following resources: 1. We release the Llama-Nemotron reasoning models -- LN-Nano, LN-Super, and LN-Ultra -- under the commercially permissive NVIDIA Open Model License Agreement. 2. We release the complete post-training dataset: Llama-Nemotron-Post-Training-Dataset. 3. We also release our training codebases: NeMo, NeMo-Aligner, and Megatron-LM.
NeMo-Inspector: A Visualization Tool for LLM Generation Analysis
May 01, 2025Abstract:Adapting Large Language Models (LLMs) to novel tasks and enhancing their overall capabilities often requires large, high-quality training datasets. Synthetic data, generated at scale, serves a valuable alternative when real-world data is scarce or difficult to obtain. However, ensuring the quality of synthetic datasets is challenging, as developers must manually inspect and refine numerous samples to identify errors and areas for improvement. This process is time-consuming and requires specialized tools. We introduce NeMo-Inspector, an open-source tool designed to simplify the analysis of synthetic datasets with integrated inference capabilities. We demonstrate its effectiveness through two real-world cases. Analysis and cleaning of the synthetically generated GSM-Plus dataset with NeMo-Inspector led to a significant decrease in low-quality samples from 46.99% to 19.51%. The tool also helped identify and correct generation errors in OpenMath models, improving accuracy by 1.92% on the MATH dataset and by 4.17% on the GSM8K dataset for a Meta-Llama-3-8B model fine-tuned on synthetic data generated from Nemotron-4-340B.
AIMO-2 Winning Solution: Building State-of-the-Art Mathematical Reasoning Models with OpenMathReasoning dataset
Apr 23, 2025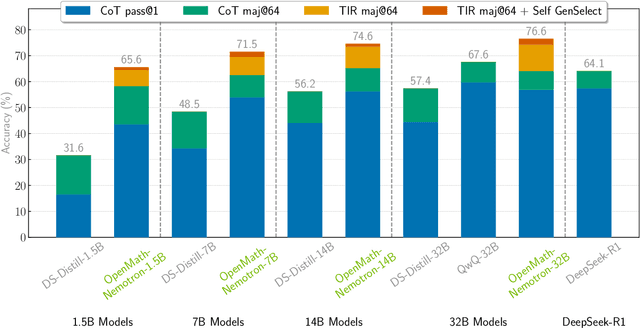
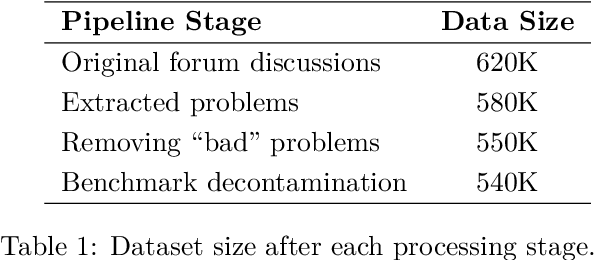

Abstract:This paper presents our winning submission to the AI Mathematical Olympiad - Progress Prize 2 (AIMO-2) competition. Our recipe for building state-of-the-art mathematical reasoning models relies on three key pillars. First, we create a large-scale dataset comprising 540K unique high-quality math problems, including olympiad-level problems, and their 3.2M long-reasoning solutions. Second, we develop a novel method to integrate code execution with long reasoning models through iterative training, generation, and quality filtering, resulting in 1.7M high-quality Tool-Integrated Reasoning solutions. Third, we create a pipeline to train models to select the most promising solution from many candidates. We show that such generative solution selection (GenSelect) can significantly improve upon majority voting baseline. Combining these ideas, we train a series of models that achieve state-of-the-art results on mathematical reasoning benchmarks. To facilitate further research, we release our code, models, and the complete OpenMathReasoning dataset under a commercially permissive license.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge