Hugo Berard
Co-Producing AI: Toward an Augmented, Participatory Lifecycle
Jul 31, 2025Abstract:Despite efforts to mitigate the inherent risks and biases of artificial intelligence (AI) algorithms, these algorithms can disproportionately impact culturally marginalized groups. A range of approaches has been proposed to address or reduce these risks, including the development of ethical guidelines and principles for responsible AI, as well as technical solutions that promote algorithmic fairness. Drawing on design justice, expansive learning theory, and recent empirical work on participatory AI, we argue that mitigating these harms requires a fundamental re-architecture of the AI production pipeline. This re-design should center co-production, diversity, equity, inclusion (DEI), and multidisciplinary collaboration. We introduce an augmented AI lifecycle consisting of five interconnected phases: co-framing, co-design, co-implementation, co-deployment, and co-maintenance. The lifecycle is informed by four multidisciplinary workshops and grounded in themes of distributed authority and iterative knowledge exchange. Finally, we relate the proposed lifecycle to several leading ethical frameworks and outline key research questions that remain for scaling participatory governance.
Negotiative Alignment: Embracing Disagreement to Achieve Fairer Outcomes -- Insights from Urban Studies
Mar 16, 2025


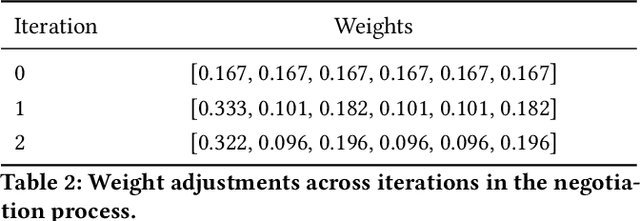
Abstract:Cities are not monolithic; they are arenas of negotiation among groups that hold varying needs, values, and experiences. Conventional methods of urban assessment -- from standardized surveys to AI-driven evaluations -- frequently rely on a single consensus metric (e.g., an average measure of inclusivity or safety). Although such aggregations simplify design decisions, they risk obscuring the distinct perspectives of marginalized populations. In this paper, we present findings from a community-centered study in Montreal involving 35 residents with diverse demographic and social identities, particularly wheelchair users, seniors, and LGBTQIA2+ individuals. Using rating and ranking tasks on 20 urban sites, we observe that disagreements are systematic rather than random, reflecting structural inequalities, differing cultural values, and personal experiences of safety and accessibility. Based on these empirical insights, we propose negotiative alignment, an AI framework that treats disagreement as an essential input to be preserved, analyzed, and addressed. Negotiative alignment builds on pluralistic models by dynamically updating stakeholder preferences through multi-agent negotiation mechanisms, ensuring no single perspective is marginalized. We outline how this framework can be integrated into urban analytics -- and other decision-making contexts -- to retain minority viewpoints, adapt to changing stakeholder concerns, and enhance fairness and accountability. The study demonstrates that preserving and engaging with disagreement, rather than striving for an artificial consensus, can produce more equitable and responsive AI-driven outcomes in urban design.
The Right to AI
Jan 29, 2025


Abstract:This paper proposes a Right to AI, which asserts that individuals and communities should meaningfully participate in the development and governance of the AI systems that shape their lives. Motivated by the increasing deployment of AI in critical domains and inspired by Henri Lefebvre's concept of the Right to the City, we reconceptualize AI as a societal infrastructure, rather than merely a product of expert design. In this paper, we critically evaluate how generative agents, large-scale data extraction, and diverse cultural values bring new complexities to AI oversight. The paper proposes that grassroots participatory methodologies can mitigate biased outcomes and enhance social responsiveness. It asserts that data is socially produced and should be managed and owned collectively. Drawing on Sherry Arnstein's Ladder of Citizen Participation and analyzing nine case studies, the paper develops a four-tier model for the Right to AI that situates the current paradigm and envisions an aspirational future. It proposes recommendations for inclusive data ownership, transparent design processes, and stakeholder-driven oversight. We also discuss market-led and state-centric alternatives and argue that participatory approaches offer a better balance between technical efficiency and democratic legitimacy.
AI-EDI-SPACE: A Co-designed Dataset for Evaluating the Quality of Public Spaces
Nov 01, 2024



Abstract:Advancements in AI heavily rely on large-scale datasets meticulously curated and annotated for training. However, concerns persist regarding the transparency and context of data collection methodologies, especially when sourced through crowdsourcing platforms. Crowdsourcing often employs low-wage workers with poor working conditions and lacks consideration for the representativeness of annotators, leading to algorithms that fail to represent diverse views and perpetuate biases against certain groups. To address these limitations, we propose a methodology involving a co-design model that actively engages stakeholders at key stages, integrating principles of Equity, Diversity, and Inclusion (EDI) to ensure diverse viewpoints. We apply this methodology to develop a dataset and AI model for evaluating public space quality using street view images, demonstrating its effectiveness in capturing diverse perspectives and fostering higher-quality data.
From Efficiency to Equity: Measuring Fairness in Preference Learning
Oct 24, 2024



Abstract:As AI systems, particularly generative models, increasingly influence decision-making, ensuring that they are able to fairly represent diverse human preferences becomes crucial. This paper introduces a novel framework for evaluating epistemic fairness in preference learning models inspired by economic theories of inequality and Rawlsian justice. We propose metrics adapted from the Gini Coefficient, Atkinson Index, and Kuznets Ratio to quantify fairness in these models. We validate our approach using two datasets: a custom visual preference dataset (AI-EDI-Space) and the Jester Jokes dataset. Our analysis reveals variations in model performance across users, highlighting potential epistemic injustices. We explore pre-processing and in-processing techniques to mitigate these inequalities, demonstrating a complex relationship between model efficiency and fairness. This work contributes to AI ethics by providing a framework for evaluating and improving epistemic fairness in preference learning models, offering insights for developing more inclusive AI systems in contexts where diverse human preferences are crucial.
Stochastic Gradient Descent-Ascent: Unified Theory and New Efficient Methods
Feb 15, 2022
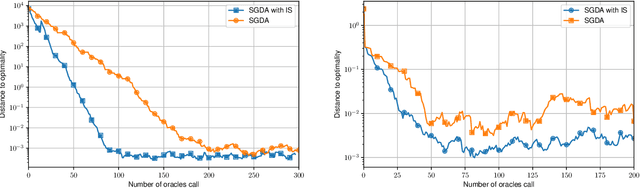
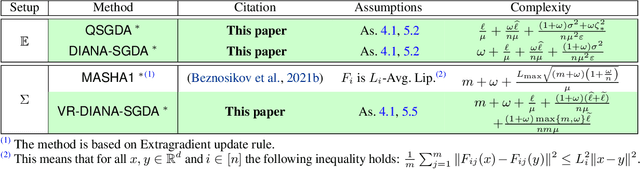
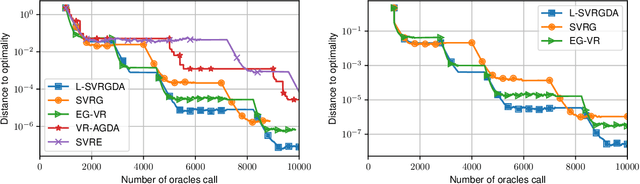
Abstract:Stochastic Gradient Descent-Ascent (SGDA) is one of the most prominent algorithms for solving min-max optimization and variational inequalities problems (VIP) appearing in various machine learning tasks. The success of the method led to several advanced extensions of the classical SGDA, including variants with arbitrary sampling, variance reduction, coordinate randomization, and distributed variants with compression, which were extensively studied in the literature, especially during the last few years. In this paper, we propose a unified convergence analysis that covers a large variety of stochastic gradient descent-ascent methods, which so far have required different intuitions, have different applications and have been developed separately in various communities. A key to our unified framework is a parametric assumption on the stochastic estimates. Via our general theoretical framework, we either recover the sharpest known rates for the known special cases or tighten them. Moreover, to illustrate the flexibility of our approach we develop several new variants of SGDA such as a new variance-reduced method (L-SVRGDA), new distributed methods with compression (QSGDA, DIANA-SGDA, VR-DIANA-SGDA), and a new method with coordinate randomization (SEGA-SGDA). Although variants of the new methods are known for solving minimization problems, they were never considered or analyzed for solving min-max problems and VIPs. We also demonstrate the most important properties of the new methods through extensive numerical experiments.
Stochastic Extragradient: General Analysis and Improved Rates
Nov 16, 2021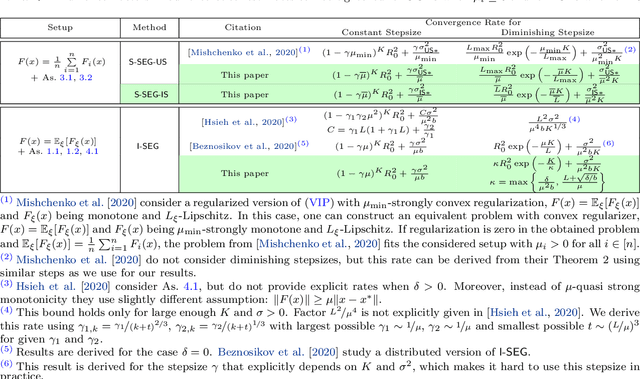
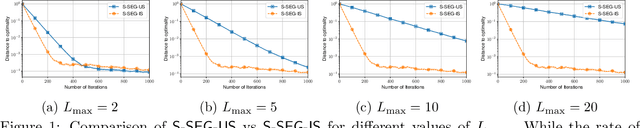
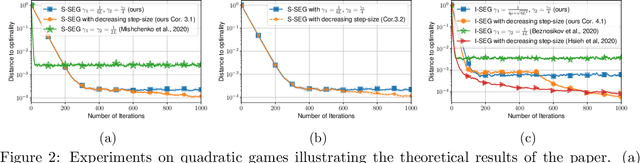

Abstract:The Stochastic Extragradient (SEG) method is one of the most popular algorithms for solving min-max optimization and variational inequalities problems (VIP) appearing in various machine learning tasks. However, several important questions regarding the convergence properties of SEG are still open, including the sampling of stochastic gradients, mini-batching, convergence guarantees for the monotone finite-sum variational inequalities with possibly non-monotone terms, and others. To address these questions, in this paper, we develop a novel theoretical framework that allows us to analyze several variants of SEG in a unified manner. Besides standard setups, like Same-Sample SEG under Lipschitzness and monotonicity or Independent-Samples SEG under uniformly bounded variance, our approach allows us to analyze variants of SEG that were never explicitly considered in the literature before. Notably, we analyze SEG with arbitrary sampling which includes importance sampling and various mini-batching strategies as special cases. Our rates for the new variants of SEG outperform the current state-of-the-art convergence guarantees and rely on less restrictive assumptions.
Stochastic Gradient Descent-Ascent and Consensus Optimization for Smooth Games: Convergence Analysis under Expected Co-coercivity
Jun 30, 2021
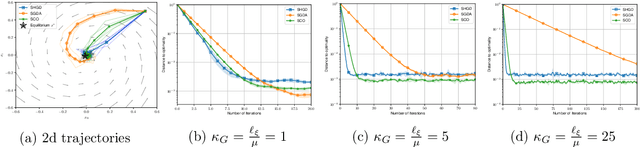
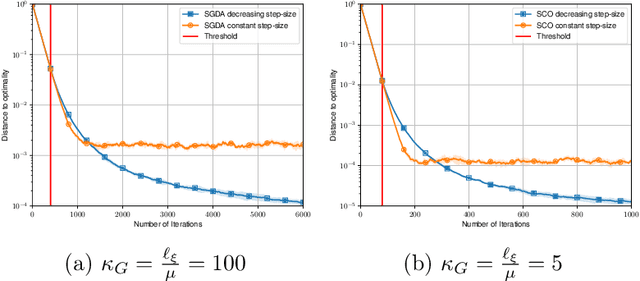

Abstract:Two of the most prominent algorithms for solving unconstrained smooth games are the classical stochastic gradient descent-ascent (SGDA) and the recently introduced stochastic consensus optimization (SCO) (Mescheder et al., 2017). SGDA is known to converge to a stationary point for specific classes of games, but current convergence analyses require a bounded variance assumption. SCO is used successfully for solving large-scale adversarial problems, but its convergence guarantees are limited to its deterministic variant. In this work, we introduce the expected co-coercivity condition, explain its benefits, and provide the first last-iterate convergence guarantees of SGDA and SCO under this condition for solving a class of stochastic variational inequality problems that are potentially non-monotone. We prove linear convergence of both methods to a neighborhood of the solution when they use constant step-size, and we propose insightful stepsize-switching rules to guarantee convergence to the exact solution. In addition, our convergence guarantees hold under the arbitrary sampling paradigm, and as such, we give insights into the complexity of minibatching.
Online Adversarial Attacks
Mar 02, 2021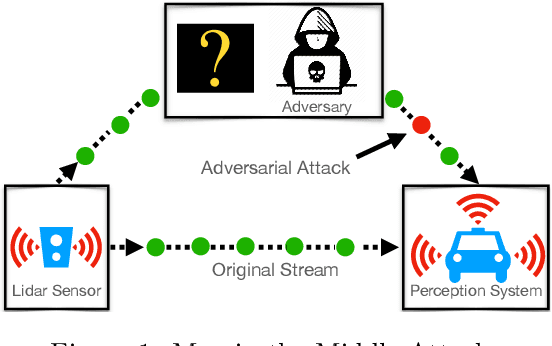
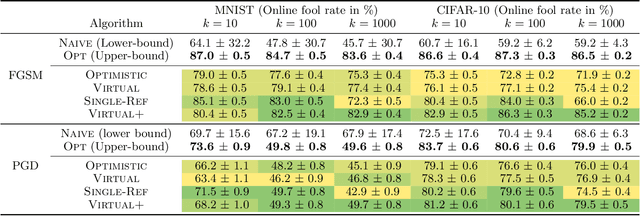
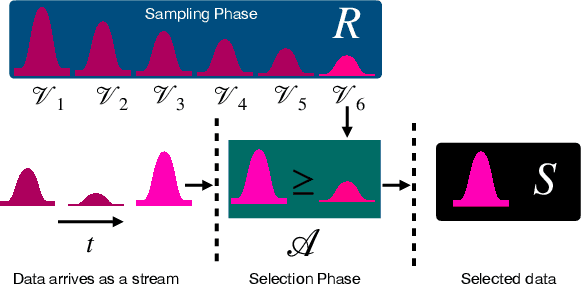
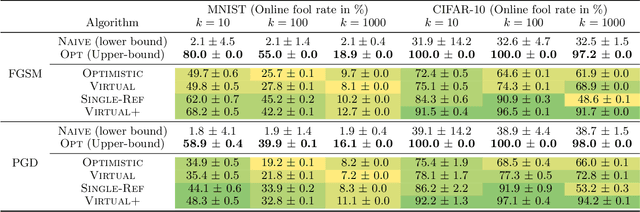
Abstract:Adversarial attacks expose important vulnerabilities of deep learning models, yet little attention has been paid to settings where data arrives as a stream. In this paper, we formalize the online adversarial attack problem, emphasizing two key elements found in real-world use-cases: attackers must operate under partial knowledge of the target model, and the decisions made by the attacker are irrevocable since they operate on a transient data stream. We first rigorously analyze a deterministic variant of the online threat model by drawing parallels to the well-studied $k$-\textit{secretary problem} and propose \algoname, a simple yet practical algorithm yielding a provably better competitive ratio for $k=2$ over the current best single threshold algorithm. We also introduce the \textit{stochastic $k$-secretary} -- effectively reducing online blackbox attacks to a $k$-secretary problem under noise -- and prove theoretical bounds on the competitive ratios of \textit{any} online algorithms adapted to this setting. Finally, we complement our theoretical results by conducting a systematic suite of experiments on MNIST and CIFAR-10 with both vanilla and robust classifiers, revealing that, by leveraging online secretary algorithms, like \algoname, we can get an online attack success rate close to the one achieved by the optimal offline solution.
Stochastic Hamiltonian Gradient Methods for Smooth Games
Jul 08, 2020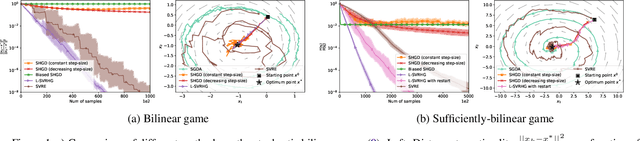

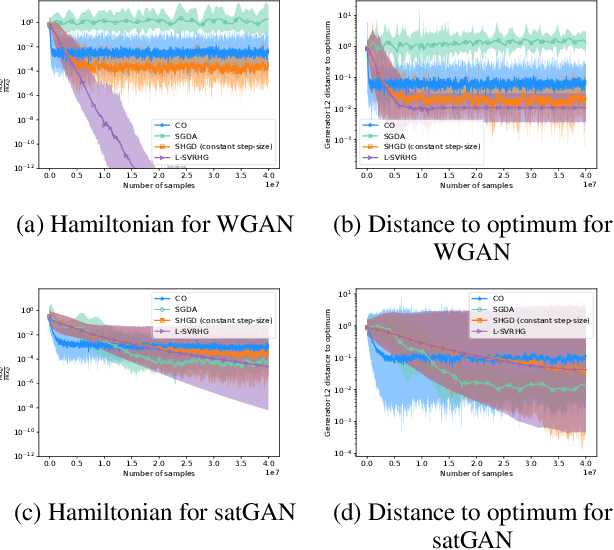

Abstract:The success of adversarial formulations in machine learning has brought renewed motivation for smooth games. In this work, we focus on the class of stochastic Hamiltonian methods and provide the first convergence guarantees for certain classes of stochastic smooth games. We propose a novel unbiased estimator for the stochastic Hamiltonian gradient descent (SHGD) and highlight its benefits. Using tools from the optimization literature we show that SHGD converges linearly to the neighbourhood of a stationary point. To guarantee convergence to the exact solution, we analyze SHGD with a decreasing step-size and we also present the first stochastic variance reduced Hamiltonian method. Our results provide the first global non-asymptotic last-iterate convergence guarantees for the class of stochastic unconstrained bilinear games and for the more general class of stochastic games that satisfy a "sufficiently bilinear" condition, notably including some non-convex non-concave problems. We supplement our analysis with experiments on stochastic bilinear and sufficiently bilinear games, where our theory is shown to be tight, and on simple adversarial machine learning formulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge