MultiXNet: Multiclass Multistage Multimodal Motion Prediction

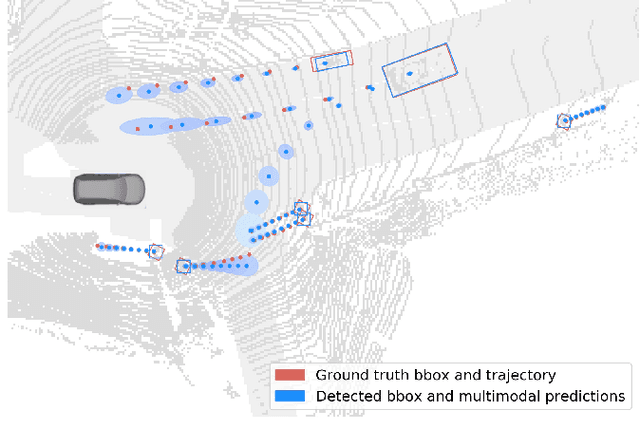
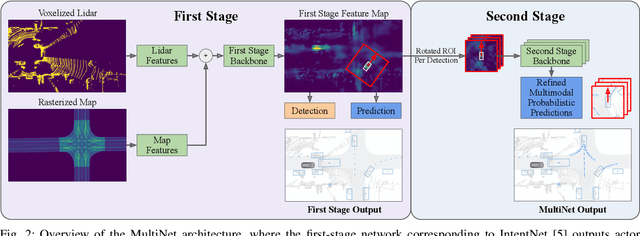
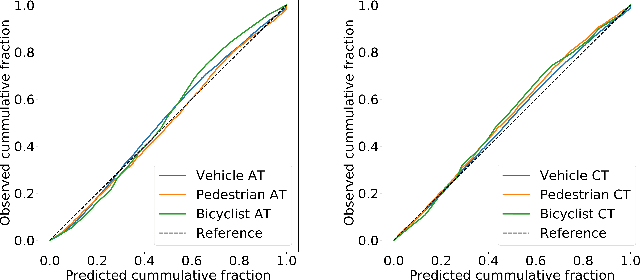
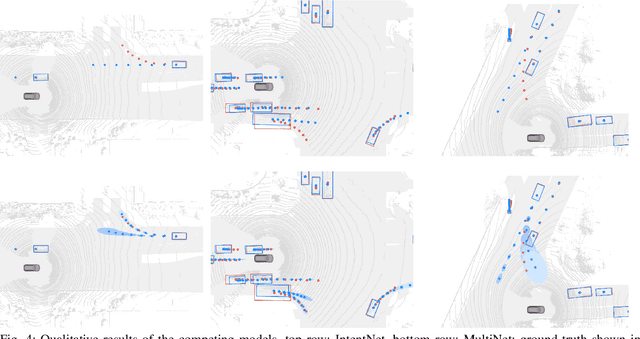
One of the critical pieces of the self-driving puzzle is understanding the surroundings of the self-driving vehicle (SDV) and predicting how these surroundings will change in the near future. To address this task we propose MultiXNet, an end-to-end approach for detection and motion prediction based directly on lidar sensor data. This approach builds on prior work by handling multiple classes of traffic actors, adding a jointly trained second-stage trajectory refinement step, and producing a multimodal probability distribution over future actor motion that includes both multiple discrete traffic behaviors and calibrated continuous uncertainties. The method was evaluated on a large-scale, real-world data set collected by a fleet of SDVs in several cities, with the results indicating that it outperforms existing state-of-the-art approaches.

Randomized Block Coordinate Descent for Online and Stochastic Optimization

Two types of low cost-per-iteration gradient descent methods have been extensively studied in parallel. One is online or stochastic gradient descent (OGD/SGD), and the other is randomzied coordinate descent (RBCD). In this paper, we combine the two types of methods together and propose online randomized block coordinate descent (ORBCD). At each iteration, ORBCD only computes the partial gradient of one block coordinate of one mini-batch samples. ORBCD is well suited for the composite minimization problem where one function is the average of the losses of a large number of samples and the other is a simple regularizer defined on high dimensional variables. We show that the iteration complexity of ORBCD has the same order as OGD or SGD. For strongly convex functions, by reducing the variance of stochastic gradients, we show that ORBCD can converge at a geometric rate in expectation, matching the convergence rate of SGD with variance reduction and RBCD.

Bregman Alternating Direction Method of Multipliers

The mirror descent algorithm (MDA) generalizes gradient descent by using a Bregman divergence to replace squared Euclidean distance. In this paper, we similarly generalize the alternating direction method of multipliers (ADMM) to Bregman ADMM (BADMM), which allows the choice of different Bregman divergences to exploit the structure of problems. BADMM provides a unified framework for ADMM and its variants, including generalized ADMM, inexact ADMM and Bethe ADMM. We establish the global convergence and the $O(1/T)$ iteration complexity for BADMM. In some cases, BADMM can be faster than ADMM by a factor of $O(n/\log(n))$. In solving the linear program of mass transportation problem, BADMM leads to massive parallelism and can easily run on GPU. BADMM is several times faster than highly optimized commercial software Gurobi.

Bethe-ADMM for Tree Decomposition based Parallel MAP Inference

We consider the problem of maximum a posteriori (MAP) inference in discrete graphical models. We present a parallel MAP inference algorithm called Bethe-ADMM based on two ideas: tree-decomposition of the graph and the alternating direction method of multipliers (ADMM). However, unlike the standard ADMM, we use an inexact ADMM augmented with a Bethe-divergence based proximal function, which makes each subproblem in ADMM easy to solve in parallel using the sum-product algorithm. We rigorously prove global convergence of Bethe-ADMM. The proposed algorithm is extensively evaluated on both synthetic and real datasets to illustrate its effectiveness. Further, the parallel Bethe-ADMM is shown to scale almost linearly with increasing number of cores.

Online Alternating Direction Method (longer version)

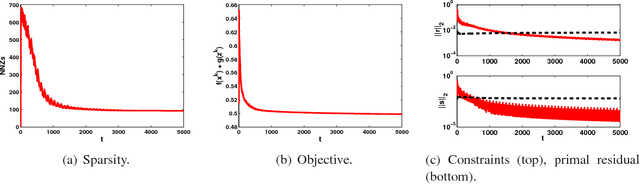
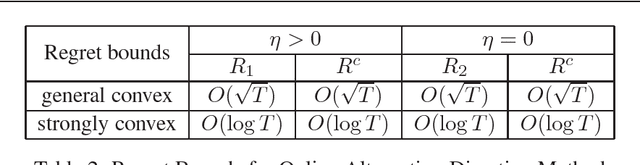
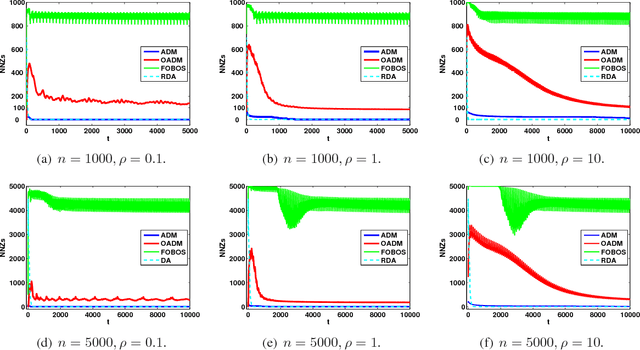
Online optimization has emerged as powerful tool in large scale optimization. In this pa- per, we introduce efficient online optimization algorithms based on the alternating direction method (ADM), which can solve online convex optimization under linear constraints where the objective could be non-smooth. We introduce new proof techniques for ADM in the batch setting, which yields a O(1/T) convergence rate for ADM and forms the basis for regret anal- ysis in the online setting. We consider two scenarios in the online setting, based on whether an additional Bregman divergence is needed or not. In both settings, we establish regret bounds for both the objective function as well as constraints violation for general and strongly convex functions. We also consider inexact ADM updates where certain terms are linearized to yield efficient updates and show the stochastic convergence rates. In addition, we briefly discuss that online ADM can be used as projection- free online learning algorithm in some scenarios. Preliminary results are presented to illustrate the performance of the proposed algorithms.

Online Alternating Direction Method

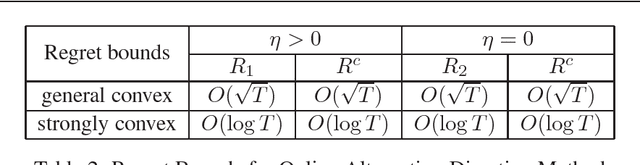
Online optimization has emerged as powerful tool in large scale optimization. In this paper, we introduce efficient online algorithms based on the alternating directions method (ADM). We introduce a new proof technique for ADM in the batch setting, which yields the O(1/T) convergence rate of ADM and forms the basis of regret analysis in the online setting. We consider two scenarios in the online setting, based on whether the solution needs to lie in the feasible set or not. In both settings, we establish regret bounds for both the objective function as well as constraint violation for general and strongly convex functions. Preliminary results are presented to illustrate the performance of the proposed algorithms.