Online Alternating Direction Method (longer version)
Paper and Code
Jul 10, 2013
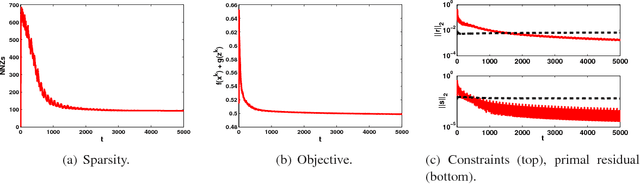
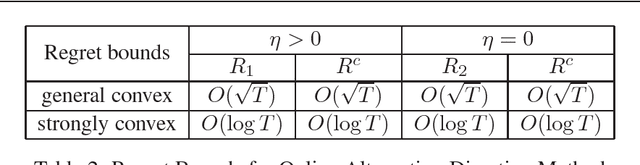
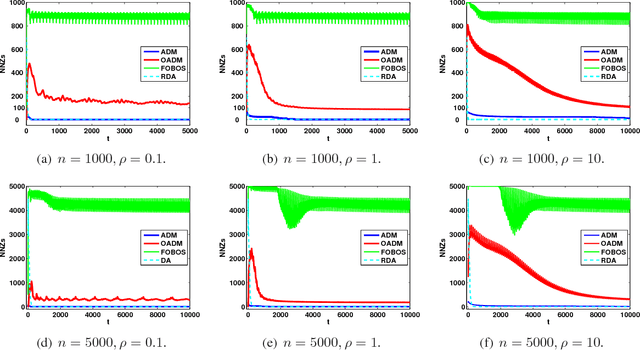
Online optimization has emerged as powerful tool in large scale optimization. In this pa- per, we introduce efficient online optimization algorithms based on the alternating direction method (ADM), which can solve online convex optimization under linear constraints where the objective could be non-smooth. We introduce new proof techniques for ADM in the batch setting, which yields a O(1/T) convergence rate for ADM and forms the basis for regret anal- ysis in the online setting. We consider two scenarios in the online setting, based on whether an additional Bregman divergence is needed or not. In both settings, we establish regret bounds for both the objective function as well as constraints violation for general and strongly convex functions. We also consider inexact ADM updates where certain terms are linearized to yield efficient updates and show the stochastic convergence rates. In addition, we briefly discuss that online ADM can be used as projection- free online learning algorithm in some scenarios. Preliminary results are presented to illustrate the performance of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge