Categorical data clustering: 25 years beyond K-modes

The clustering of categorical data is a common and important task in computer science, offering profound implications across a spectrum of applications. Unlike purely numerical datasets, categorical data often lack inherent ordering as in nominal data, or have varying levels of order as in ordinal data, thus requiring specialized methodologies for efficient organization and analysis. This review provides a comprehensive synthesis of categorical data clustering in the past twenty-five years, starting from the introduction of K-modes. It elucidates the pivotal role of categorical data clustering in diverse fields such as health sciences, natural sciences, social sciences, education, engineering and economics. Practical comparisons are conducted for algorithms having public implementations, highlighting distinguishing clustering methodologies and revealing the performance of recent algorithms on several benchmark categorical datasets. Finally, challenges and opportunities in the field are discussed.

Function Decomposition Tree with Causality-First Perspective and Systematic Description of Problems in Materials Informatics

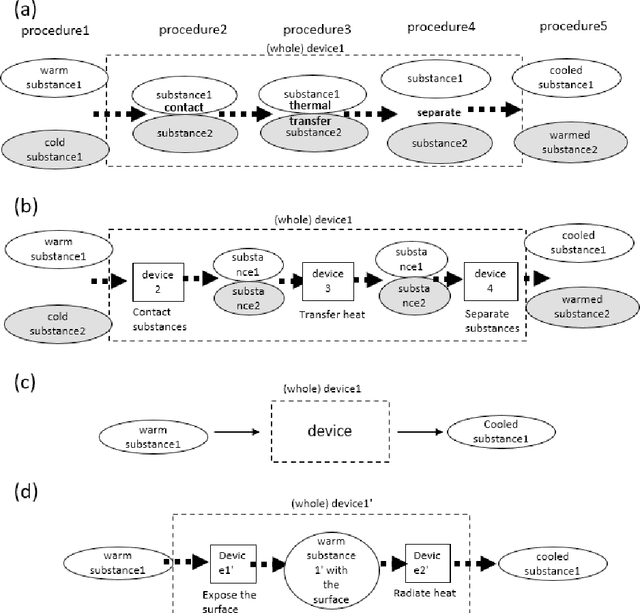
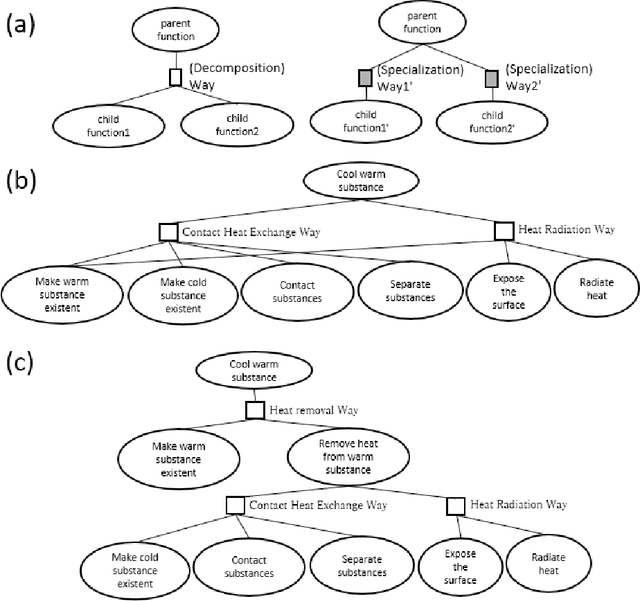
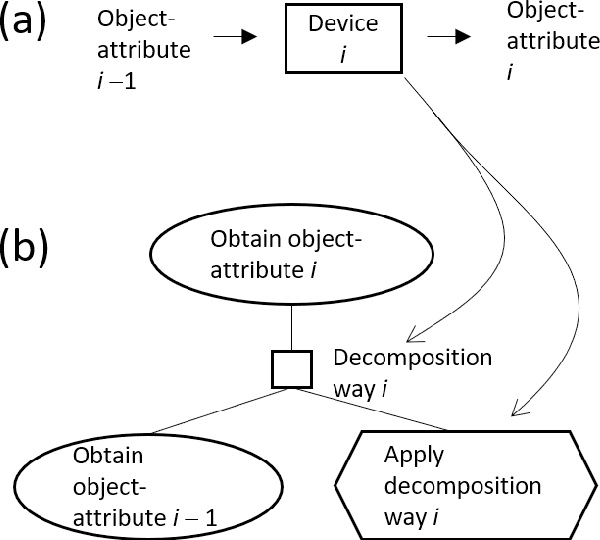
As interdisciplinary science is flourishing because of materials informatics and additional factors; a systematic way is required for expressing knowledge and facilitating communication between scientists in various fields. A function decomposition tree is such a representation, but domain scientists face difficulty in constructing it. Thus, this study cites the general problems encountered by beginners in generating function decomposition trees and proposes a new function decomposition representation method based on a causality-first perspective for resolution of these problems. The causality-first decomposition tree was obtained from a workflow expressed according to the processing sequence. Moreover, we developed a program that performed automatic conversion using the features of the causality-first decomposition trees. The proposed method was applied to materials informatics to demonstrate the systematic representation of expert knowledge and its usefullness.

Ensemble learning reveals dissimilarity between rare-earth transition metal binary alloys with respect to the Curie temperature

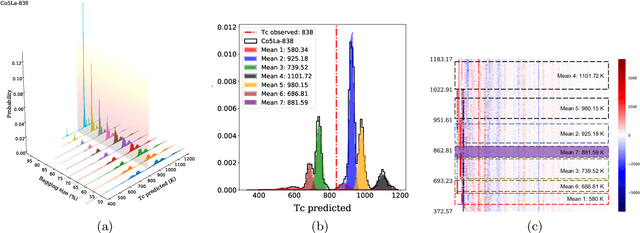
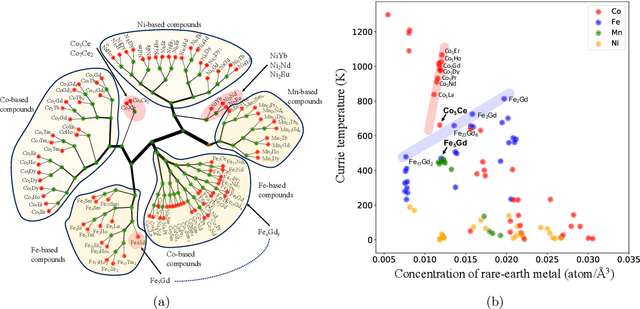
We propose a data-driven method to extract dissimilarity between materials, with respect to a given target physical property. The technique is based on an ensemble method with Kernel ridge regression as the predicting model; multiple random subset sampling of the materials is done to generate prediction models and the corresponding contributions of the reference training materials in detail. The distribution of the predicted values for each material can be approximated by a Gaussian mixture model. The reference training materials contributed to the prediction model that accurately predicts the physical property value of a specific material, are considered to be similar to that material, or vice versa. Evaluations using synthesized data demonstrate that the proposed method can effectively measure the dissimilarity between data instances. An application of the analysis method on the data of Curie temperature (TC) of binary 3d transition metal 4f rare earth binary alloys also reveals meaningful results on the relations between the materials. The proposed method can be considered as a potential tool for obtaining a deeper understanding of the structure of data, with respect to a target property, in particular.

HyperVAE: A Minimum Description Length Variational Hyper-Encoding Network

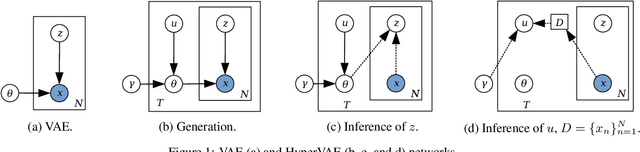
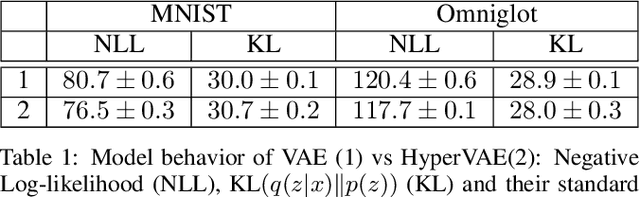
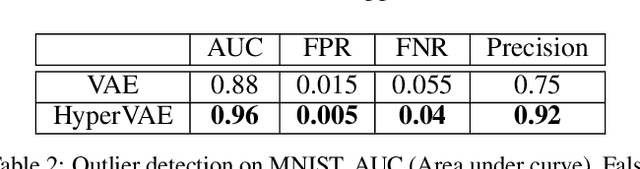
We propose a framework called HyperVAE for encoding distributions of distributions. When a target distribution is modeled by a VAE, its neural network parameters \theta is drawn from a distribution p(\theta) which is modeled by a hyper-level VAE. We propose a variational inference using Gaussian mixture models to implicitly encode the parameters \theta into a low dimensional Gaussian distribution. Given a target distribution, we predict the posterior distribution of the latent code, then use a matrix-network decoder to generate a posterior distribution q(\theta). HyperVAE can encode the parameters \theta in full in contrast to common hyper-networks practices, which generate only the scale and bias vectors as target-network parameters. Thus HyperVAE preserves much more information about the model for each task in the latent space. We discuss HyperVAE using the minimum description length (MDL) principle and show that it helps HyperVAE to generalize. We evaluate HyperVAE in density estimation tasks, outlier detection and discovery of novel design classes, demonstrating its efficacy.

Measuring the Similarity between Materials with an Emphasis on the Materials Distinctiveness

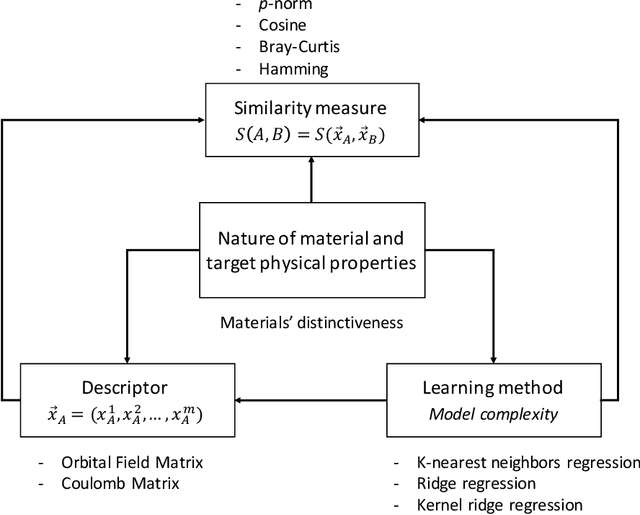
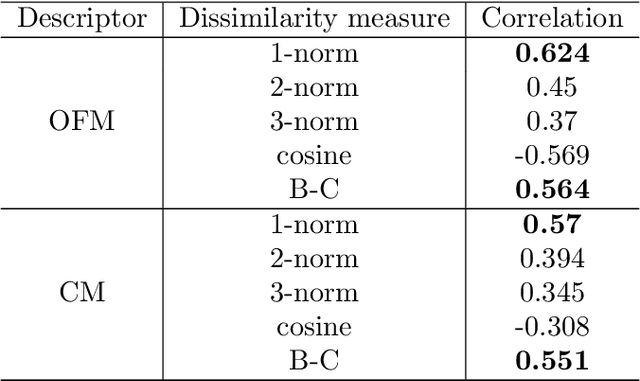
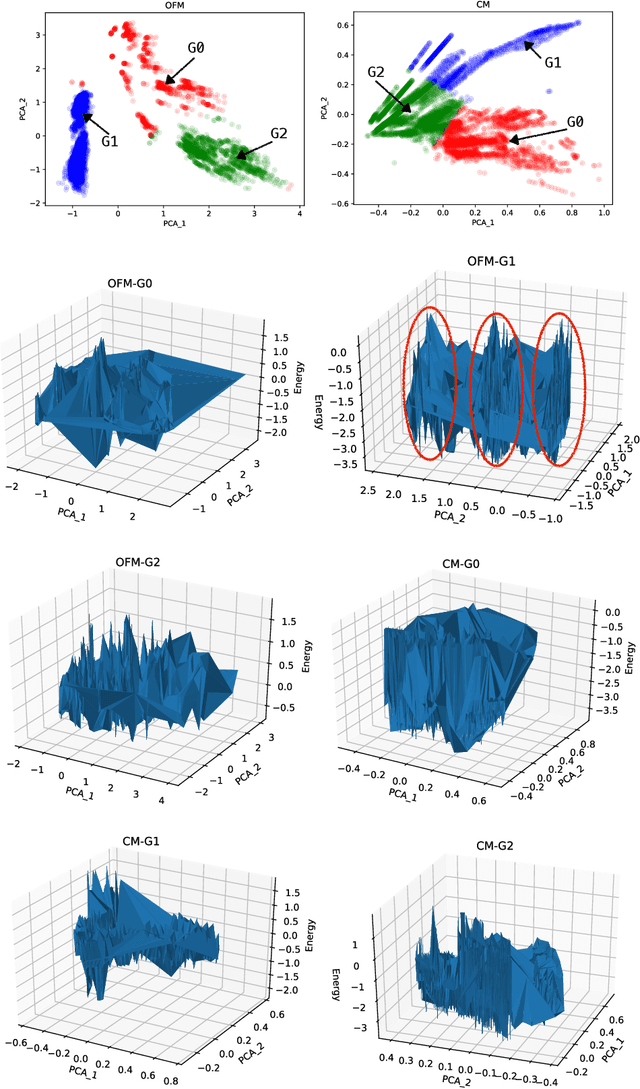
In this study, we establish a basis for selecting similarity measures when applying machine learning techniques to solve materials science problems. This selection is considered with an emphasis on the distinctiveness between materials that reflect their nature well. We perform a case study with a dataset of rare-earth transition metal crystalline compounds represented using the Orbital Field Matrix descriptor and the Coulomb Matrix descriptor. We perform predictions of the formation energies using k-nearest neighbors regression, ridge regression, and kernel ridge regression. Through detailed analyses of the yield prediction accuracy, we examine the relationship between the characteristics of the material representation and similarity measures, and the complexity of the energy function they can capture. Empirical experiments and theoretical analysis reveal that similarity measures and kernels that minimize the loss of materials distinctiveness improve the prediction performance.